В последние годы вопрос повышения эффективности процесса резания становится все актуальнее, в связи с растущей конкуренций на рынке сбыта и непрерывными попытками борьбы с потерями на производстве [1]. Одним из новых методов в деревообрабатывающей промышленности является повсеместное использование ультразвукового излучения для различных целей [2]. Ультразвук в технологических операциях деревопереработки возможно использовать как для создания принципиально новых технологических решений, так и для использования совместно с существующими [3]. Высокая эффективность ультразвуковых воздействий на различные технологические процессы и образование новых подтверждена многочисленными исследованиями и опытом более чем тридцатилетнего применения на ряде предприятий различных отраслей промышленности [4].
В процессе резания инструмент подвергается мощным механическим, температурным, химическим и трибологическим воздействиям [5]. Обычный процесс резания (МПР) обусловлен высокой температурой резания, большими усилиями резания и последующим быстрым износом инструмента даже при относительно низкой скорости резания. Эти проблемы в конечном итоге приводят к ухудшению качества обработки и препятствуют увеличению скорости резания, что снижает эффективность обработки. Чтобы преодолеть эти проблемы и получить высококачественные заготовки после обработки дорогостоящих материалов, применяется множество новых передовых технологий обработки, использующих добавление в процесс резания различных внешних источников энергии для оказания помощи в механической обработке, среди которых добавление ультразвуковых колебаний (УЗПР) является одним из приоритетных [6]. Несмотря на то что применение ультразвуковых колебаний показало хорошие экспериментальные результаты, данный процесс все еще находится на начальном этапе развития и нуждается в дальнейших обширных исследованиях.
УЗПР добавляет управляемые синусоидальные колебания инструмента к процессу МПР [7]. Для применения УЗПР необходимо контакт «инструмент – заготовка» сделать прерывистым, что приносит много преимуществ по сравнению с МПР по качеству и эффективности обработки, включая уменьшение усилий режущего инструмента [7], увеличенный срок службы инструмента [8], улучшенное удаление материала [9], уменьшенную шероховатость поверхности и улучшенную точность формы [7].
Многие исследователи вели научный поиск обоснований того, почему УЗПР может эффективно улучшить качество обработки и повысить эффективность обработки [10]. Одно из возможных объяснений заключается в том, что УЗПР может повысить стабильность резания и подавить вибрацию по сравнению с МПР, таким образом, что срез заготовки может получить более высокую точность и лучшую шероховатость поверхности после механической обработки [11], а для увеличения скорости удаления стружки можно использовать большую глубину резки. Тем не менее существующих данных недостаточно для того чтобы дать конкретное заключение о том, в каком диапазоне контролируемых параметров механическая обработка с ультразвуковыми колебаниями могла бы стабильно обеспечить более высокую стабильность резания. В исследовании [12] автор попытался составить диаграмму устойчивости процесса резания (УПР) для УЗПР с использованием обычного метода частотной области. Однако автор сделал временную задержку τ равной периоду времени Т в своем анализе, что очень ограничено, поскольку τ определяется скоростью режущего инструмента, которая является изменяемой, а Т определяется частотой колебаний, которая почти фиксируется на резонансной частоте режущего инструмента в УЗПР. Они не всегда равны, и этот традиционный метод не может быть использован для анализа влияния частоты вибрации на стабильность резания. На самом деле было доказано, что несколько методов применимы для прогнозирования устойчивости при обычном точении или фрезеровании, таких как метод полудискретизации [13] и метод полной дискретизации [14], и эти методы могут быть успешно использованы для прогнозирования устойчивости в УЗПР с некоторыми исключениями.
В этой статье основное внимание уделяется поведению устойчивости УЗПР и сравнивается с анализом МПР, чтобы лучше понять эффект подавления вибрации УЗПР.
Анализ усилий, возникающих во время резания с ультразвуковыми колебаниями
1. Анализ кинематических нагрузок во время резания.
На рис. 1, а и б, показаны смещение и скорость инструмента относительно заготовки во времени t, а на рис. 1, в, показан механизм генерации пульсирующих сил резания в УЗПР. В одном цикле колебаний T (от t1 до t4) силы резания существуют только в зоне TC (от t3 до t4). Значения сил при резке равны значениям в СМ, так как наложенные колебания в значительной степени не влияют на поведение заготовки и изменяют только прикладываемые усилия. При отсутствии контакта инструмента с заготовкой силы резания отсутствуют (от t1 до t3), поэтому средние силы уменьшаются, по сравнению с МПР.
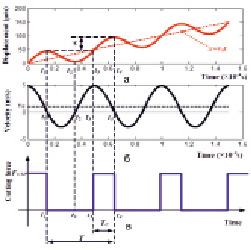
Рис. 1. (a) Относительное смещение заготовки, (б) относительная скорость заготовки инструмента, (в) механизм пульсирующих усилий резания
Поскольку силы резания тесно связаны с временем резания в УЗПР, мы определяем показатель «r», названный рабочим циклом:
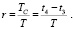 (1)
(1)
Тогда введем периодическую функцию g(t):
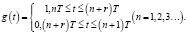 (2)
(2)
Силы в УЗПР можно выразить в виде (3), где FУЗПР представляет собой сумму сил резания в УЗПР, тогда как FМПР – сумма сил в МПР.
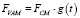 . (3)
. (3)
FМПР получен с использованием модели плоскости сдвига [15, 16], включая усилие в направлении FC и направлении подачи FT, как выражено в уравнении (4) и (5) где h – недеформированная толщина стружки, w – ширина разреза, KC и KT – константы резания, которые могут быть предсказаны аналитически, используя расширенную теорию механической обработки Оксли с моделью стресса потока Джонсона и Кука [18].
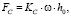 (4)
(4)
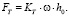 (5)
(5)
В итоге силы резания в УЗПР получаю путем объединения уравнений (1–5).
2. Проверка теоретических данных методом конечных элементов.
Ниже приводится пример исследования, показывающего последовательность расчета и результат, математическую модель усилий резания. AlMg 5053 используется в качестве материала заготовки, а параметры давления потока Джонсона – Кука и некоторые дополнительные свойства материала, используемые в модели. Условия резания, параметры вибрации и геометрия инструмента следующие: номинальная скорость резания 60 м/мин, скорость подачи 0,15 мм/об., глубина разреза 0,2 мм; частота вибрации 20 кГц, амплитуда колебаний 20 мкм; угол поворота 0 градусов, угол зазора 7 градусов. Результаты расчета приведены в табл. 1.
Таблица 1
Результаты расчета
|
Показатель |
KC, (МПа) |
KT, (МПа) |
r |
T, сек*10-3 |
|
Значение |
2,1е3 |
1,2е3 |
0,4095 |
0,05 |
На рис. 2 сравниваются силы, рассчитанные на основе математической модели и рассчитанные методом конечных элементов (МКЭ), в (а) направлении резания и (б) направлении подачи. Черные пунктирные линии представляют собой полученные данные на основе математической модели, а красные сплошные линии представляют результаты, собранные МКЭ. Из рис. 2 видно, что пунктирные линии и непрерывные линии хорошо согласуются с учетом максимального значения и изменяющегося тренда в обоих направлениях, что подтверждает правильность предложенной модели силы. Кроме того, средние силы резания в УЗПР рассчитываются в обоих направлениях. Используя предложенную математическую модель, средние силы резания составляют 24,2 Н в направлении резания и 13,3 Н в направлении подачи, а по МКЭ соответствующие цифры составляют 27,4 Н и 14,6 Н соответственно. Различия между этими двумя методами составляют не более 5 %.
Математическая модель ультразвукового колебания и состояния стабильности
1. Математическая модель стабильности резания для УЗПР.
На рис. 3 показан механизм вибрации в момент касания режущего инструмента заготовки. Как правило, система резания рассматривается как единая свободная система, предполагая, что инструмент является подвижным в направлении подачи, в то время как заготовка является неподвижной.
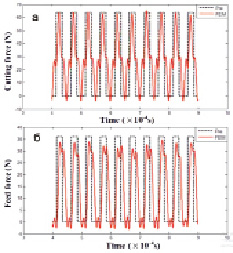
Рис. 2. Сравнение сил, расчитанных по математической модели и МКЭ в (а) – направлении резания и (б) – направлении подачи
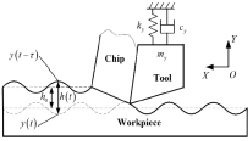
Рис. 3. Механизм вибрации в момент касания режущего инструмента заготовки
Зависимая от времени, мгновенная недеформированная толщина стружки h(t) определяется предполагаемой толщиной стружки и предшествующими и текущими колебаниями:
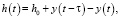 (6)
(6)
где τ – время одного реза, y(t – τ) и y(t) – колебания в предыдущем и текущем оборотах соответственно. Подставляя (3) и (5) в уравнение (6), динамическая сила резания в направлении подачи в УЗПР выражается следующим образом:
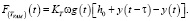 (7)
(7)
Наконец, динамическое уравнение для УЗПР получено с учетом массы my, демпфирования cy и жесткости ky одного реза:
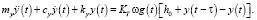 (8)
(8)
2 Анализ стабильности вибрационной обработки.
Предполагаемая толщина стружки не влияет на стабильность системы [13, 14], поэтому это значение можно опустить для простоты анализа стабильности и уравнения, (8) становится:
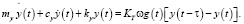 (9)
(9)
Пусть 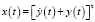 , тогда пространственно-временная форма уравнения (9) получится:
, тогда пространственно-временная форма уравнения (9) получится:
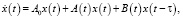 (10)
(10)
где
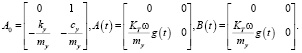 (11)
(11)
Стабильность прогнозируется с использованием метода полной дискретизации [12]. Дискретизируем период времени T на n равных интервалов, то есть T = nΔt, и введем другое целое число m, которое соответствует: 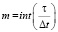 . На каждом временном интервале
. На каждом временном интервале 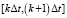 , ответ уравнения (10) с начальным условием
, ответ уравнения (10) с начальным условием 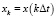 можно получить следующее:
можно получить следующее:
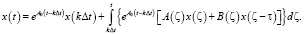 (12)
(12)
Тогда можно получить 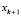 , то есть
, то есть 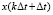 :
:
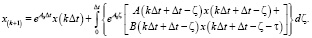 (13)
(13)
Затем элемент времени 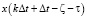 , элемент состояния
, элемент состояния 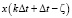 , временные элементы
, временные элементы 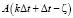 и
и 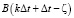 аппроксимируются линейно с использованием граничных значений:
аппроксимируются линейно с использованием граничных значений:
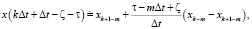 (14)
(14)
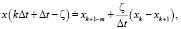 (15)
(15)
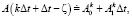 (16)
(16)
где 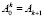 ,
, 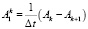 , и Ak – значение A(t) за время kΔt
, и Ak – значение A(t) за время kΔt
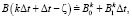 (17)
(17)
где 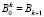 ,
, 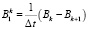 , и Bk – значение B(t) за время kΔt.
, и Bk – значение B(t) за время kΔt.
Подставим уравнение (14–17) в уравнение (13), 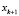 можно записать в виде
можно записать в виде
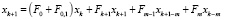 (18)
(18)
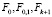 те же, что и в [13], тогда как
те же, что и в [13], тогда как 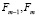 выражаются как
выражаются как
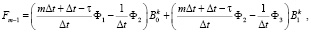 (19)
(19)
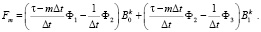 (20)
(20)
Согласно (18), дискретное отображение можно определить как
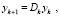 (21)
(21)
где вектор yk и Dk определяются следующим образом.
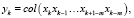 (22)
(22)
 (23)
(23)
Определим матрицу перехода Ф, а затем получим следующие уравнения:
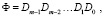 (24)
(24)
y = Фy0. (25)
Согласно теории Флоке [17], устойчивость системы определяется следующим образом: если модули всех собственных значений Ф меньше единицы, система устойчива; в противном случае система нестабильна.
3. Пример расчета и проверки с помощью моделирования во временной области.
Ниже приведен пример получения диаграммы лепестков устойчивости для УЗПР, используя метод, упомянутый в вышеуказанном подразделе, и проведено сравнение с соответствующим поведением устойчивости в МПР. Параметры анализа устойчивости перечислены в табл. 2.
Таблица 2
Параметры для анализа стабильности
|
Показатель |
Частота, Гц |
Жесткость, Н/м |
Коэф. сжатия |
KT, MPa |
r |
|
Значение |
228,8 |
2,26e8 |
0,01 |
850 |
0,6 |
На рис. 4 показана полученная диаграмма стабильности МПР (показана черной линией) и УЗПР (показана красной линией). Очевидно, что красная линия находится выше черной линии под любой скоростью режущего инструмента в исследуемой области, что означает, что УЗПР всегда может оказывать положительное влияние на стабильность резания. Диаграмма стабильности для МПР та же, что и результат [12], однако диаграмма устойчивости УЗПР показывает другой результат. В [12], при скорости вращения режущего инструмента 1400 об/мин, допустимая глубина разреза в УЗПР меньше, чем в МПР, что противоречит рис. 4. Чтобы проверить результат прогнозирования стабильности в этой статье, стандартное моделирование во временной области выполняется со скоростью режущего инструмента 1400 об/мин.
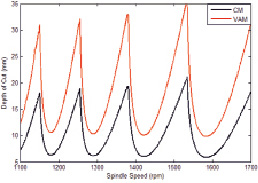
Рис. 4. Диаграмма устойчивости МПР и УЗПР
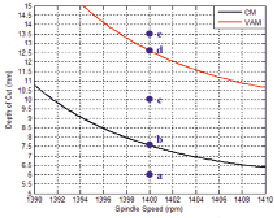
Рис. 5. Подробная диаграмма устойчивости режущего инструмента на скорости 1400 об/мин
Рис. 4 строится для скорости режущего инструмента равной 1400 об/мин, чтобы увидеть больше деталей, как показано на рис. 5. На рис. 5 изображены пять различных точек a–e, представляющих разную глубину разреза, среди которых точка b и точка d находятся на границе устойчивости. Следующий этап моделирования во временной области выполняется в этих пяти точках, и результаты показаны на рис. 6.
На рис. 6, а, как МПР, так и УЗПР стабильны, а колебания в УЗПР намного ниже и сходятся быстрее. На рис. 6, б, МПР становится критическим, колебания почти остаются неизменными, тогда как УЗПР остается достаточно стабильным. Это явление соответствует прогнозируемому результату на рис. 5: точка b находится на черной линии, которая является границей для отделения стабильной и неустойчивой области для МПР. Однако точка b намного ниже красной линии, что означает, что она находится в стабильной области в УЗПР. На рис. 6, в, МПР становится довольно неустойчивым, а колебания превышают допустимые значения через определенный интервал времени. И если глубина резки увеличивается непрерывно, колебания будут становиться выше, что показано на рис. 6, г, и на рис. 6, д. Для УЗПР он все еще стабилен на рис. 6, в. Только когда глубина разреза достигает около 12,5 мм, он становится критически устойчивым, как показано на рис. 6, г, и увеличение глубины разреза непрерывно до 13,5 мм приводит к неустойчивости, как показано на рис. 6, д. Следует отметить, что независимо от стабильности колебания в УЗПР всегда ниже, чем в МПР. Вышеуказанные результаты моделирования хорошо согласуются с диаграммой лепестков устойчивости, показанной на рис. 5, которая подтверждает ее правильность.
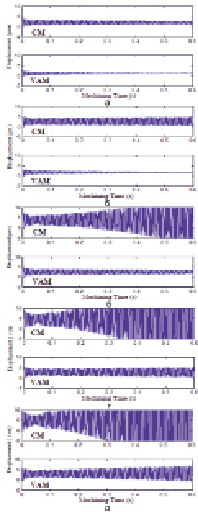
Рис. 6. Моделирование во временной области при разных условиях резания
Выводы
В этой статье предлагается математическая модель прогнозируемых сил резания, возникающих в УЗПР, и эта модель оказалась точной по сравнению с МКЭ. Анализ устойчивости, основанный на этой модели, проводится для сравнения разницы в поведении устойчивости между МПР и УЗПР. Из полученной диаграммы состояния стабильности выясняется, что УЗПР может эффективно увеличивать допустимую глубину резки, что означает, что она имеет более высокую устойчивость к резанию.
Настоящая статья дает теоретические основы анализа стабильности для УЗПР, и результаты полностью подтверждают его преимущества по качеству обработки и эффективности обработки.
Библиографическая ссылка
Чикишев Е.В., Гаспарян Г.Д. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ПРОЦЕССА РЕЗАНИЯ С ПРИМЕНЕНИЕМ УЛЬТРАЗВУКОВЫХ КОЛЕБАНИЙ И АНАЛИЗ УСТОЙЧИВОСТИ ПРОЦЕССА // Современные наукоемкие технологии. 2018. № 7. С. 142-149;URL: https://top-technologies.ru/ru/article/view?id=37094 (дата обращения: 15.02.2026).



