В строительстве, как на поверхности суши, так и на воде, иногда происходят ситуации, когда свая входит в грунт не вертикально, проникание сваи не соответствует требованиям СНИПов. В этих ситуациях, если возможно, устанавливается дублирующая свая, а первая спиливается. Принципиальная схема извлечения свай из грунта с твердой поверхности с помощью артиллерийских систем приведена в работах [1, 2]. Но этот процесс сложен в условиях строительства на воде. В результате чего или перерабатывается проект строительства и устанавливается новая свая, или проводится извлечение из грунта невертикальной сваи. Но извлечение довольно трудоемко, особенно если свая устанавливалась на глубине воды, большей, чем длина сваи. Поэтому разработка установки, которая позволила бы извлекать сваю из донного грунта на любой глубине, крайне важна.
Целью статьи является описание принципиальной схемы и математической модели установки, позволяющей извлекать сваи из донного грунта с понтона, находящегося на поверхности спокойной воды, то есть при отсутствии колебаний понтона.
Схема и принцип работы установки, извлекающей сваю из донного грунта
На рис. 1 представлена схема установки, извлекающей сваю из донного грунта.
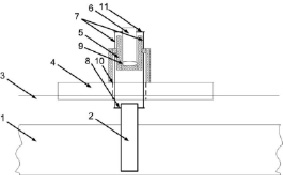
Рис. 1. Принципиальная схема установки, извлекающей сваю из донного грунта, где 1 – донный грунт, 2 – свая, 3 – поверхность воды, 4 – понтон с отверстием в центре, 5 – артиллерийское орудие с креплением к понтону, 6 – поршень, 7 – трос, 8 – крепежный элемент в свае, 9 – камора с порохом, 10 – отверстие в понтоне, 11 – крепежный элемент в поршне
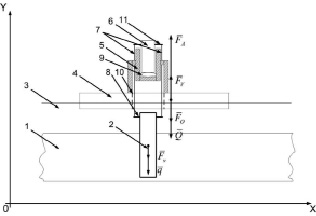
Рис. 2. Схема положения системы в момент выстрела, где 1 – донный грунт, 2 – свая, 3 – поверхность воды, 4 – понтон с отверстием в центре, 5 – артиллерийское орудие с креплением к понтону, 6 – поршень, 7 – трос, 8 – крепежный элемент в свае, 9 – камора с порохом, 10 – отверстие в понтоне, 11 – крепежный элемент в поршне,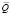 
– вес артиллерийского орудия с платформой, 
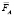– сила Архимеда, действующая на платформу, 
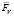– сила сопротивления движению платформы, 
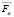– сила отдачи артиллерийского орудия, 
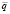– вес строительного элемента, 
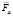– сила Архимеда, действующая на строительный элемент, 
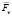– сила сопротивления движению строительного элемента
Принцип действия установки следующий: для извлечения сваи 2 из донного грунта 1 необходимо изначально, чтобы ее высота была ниже уровня днища понтона 4. Поэтому первоначально при необходимости проводятся работы по уменьшению длины сваи 2, чтобы возможно было поместить понтон 4 над ней. Далее в свае 2 необходимо сделать закладные для крепления крепежного элемента 8 и установить его. После этого подводят понтон 4 так, чтобы свая 2 оказалась по центру отверстия 10 и закрепляют понтон 4 в таком положении. На следующем шаге скрепляют крепежный элемент 8 в свае 2 и крепежный элемент 11 в поршне 6 при помощи тросов 7. Далее производится выстрел из артиллерийского орудия 5 поршнем 6. Если свая выходит не полностью из грунта, то повторяют весь процесс, начиная с подготовительного этапа.
Математическая модель извлечения сваи из донного грунта
Первоначально необходимо определиться с основными допущениями. К допущениям, описанным в работе [3] для процесса погружения свай в донный грунт с помощью артиллерийского орудия, нужно добавить следующие:
1) крепежный элемент в поршне и свае – недеформируемое тело;
2) поршень – недеформируемое тело;
3) трос, соединяющий крепежные элементы – недеформируемое тело;
4) m1 – масса поршня;
5) сила Архимеда, действующая на сваю мала по сравнению с другими силами;
6) свая погружена в донный грунт вертикально, допускаемое отклонение от вертикали – не более 5 град;
7) верхняя часть сваи находится на уровне с поверхностью воды.
Рассмотрим силы, действующие на систему «артиллерийское орудие – понтон – свая» в момент выстрела. На рис. 2 представлена схема установки с описанием сил, действующих на систему.
Для представленной схемы извлечения из грунта строительного элемента будем рассматривать, как и в работах [4, 5], пять этапов: первый этап – предварительный период выстрела; второй этап – первый период выстрела, движение поршня и сваи вверх и артиллерийского орудия с платформой вниз; третий этап – второй период выстрела, движение поршня и сваи вверх и артиллерийского орудия с платформой вниз; четвертый этап – движение поршня и сваи вверх; пятый этап – колебание артиллерийского орудия с платформой.
На первом этапе извлечения сваи из донного грунта уравнение для определения относительной части сгоревшего пороха будет иметь вид [6]:
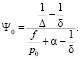
Для второго этапа погружения сваи система уравнений будет иметь вид
,
,
.
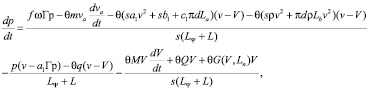
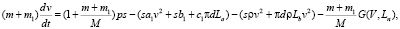
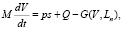
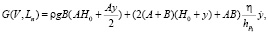
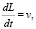
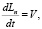
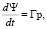
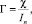
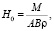
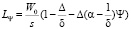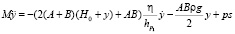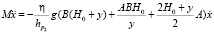Начальные условия для системы уравнений следующие: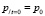 
, 
, 
, 
, 
, 
, 
, 
, 
, 
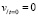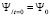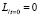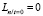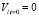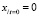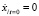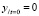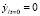– координаты точки положения системы до выстрела.
Для третьего этапа система уравнений будет следующая:
, 
,
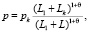
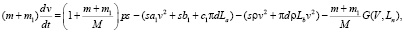
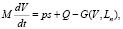
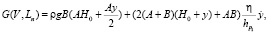
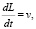
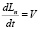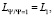
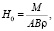
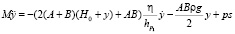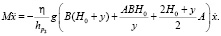
Начальными условиями для системы уравнений будут полученные значения переменных р(t), v(t), V(t), L(t), Ln(t), x(t),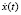 
, y(t), 
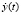решения системы уравнений в конце второго этапа.
Для четвертого этапа приведем следующие уравнения:
, 
,
.
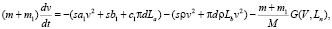
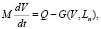
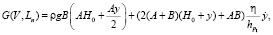
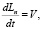
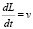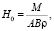
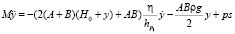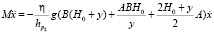Начальными условиями для системы уравнений будут полученные значения переменных v(t), V(t), L(t), Ln(t), x(t),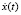 
, y(t), 
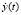решения системы уравнений в конце третьего этапа.
После выхода поршня из ствола артиллерийского орудия наступает пятый этап, при этом этапе платформа продолжает колебательное движение, описываемое задачей Коши:
, 
.
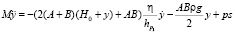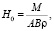
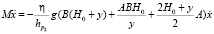Начальными условиями для системы уравнений будут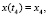 
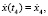
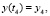
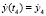, где t4 – время конца четвертого этапа, 
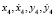– значение соответствующих переменных в конце четвертого этапа.
Условные обозначения, принятые в системе уравнений: Ψ0 – относительной части сгоревшего пороха до начала движения строительного элемента, Δ – плотность заряжания, δ – плотность пороха, f – сила пороха, p0 – давление форсирования строительного элемента, p – давление в стволе, создаваемое пороховыми газами, t – время прохождения процесса извлечения сваи, α – коволюм пороховых газов,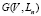 
– общая сила тормозов отката, s – площадь поперечного сечения ствола, pk, Lk – значения давления в канале ствола и пути строительного элемента к концу первого периода выстрела, L, v – путь поршня (сваи) по каналу ствола и его скорость относительно канала ствола, Ln, V – перемещение и скорость артиллерийского орудия с платформой, Ls – длина ствола артиллерийского орудия, m – масса сваи, m1 – масса поршня, L0 – длина строительного элемента, La – величина начального заглубления сваи, Lb – величина начальной части сваи, находящейся в воде, d – калибр ствола, W0 – объем каморы, ω – масса заряда, χ – характеристика формы пороха, In – полный импульс давления газов во время сгорания пороха, θ – коэффициент адиабаты без единиц, Q1 – вес откатных частей орудия, D – диаметр головной части сваи, Qp – вес платформы, A, B, H0 – линейные размеры платформы, погруженные в воду, ρ – плотность воды, Il – показатель консистенции для глины, a1, b1, c1 – коэффициенты сопротивления глинистого грунта.
Отметим то, что полученные системы дифференциальных уравнений при сделанных в начале статьи допущениях полностью описывают динамику извлечения сваи из донного грунта с помощью артиллерийской системы, принципиальная схема которой изображена на рис. 1.
Рассмотрим численный эксперимент, основанный на построенной математической модели.
Численный эксперимент
Рассмотрим один пример решения задачи для конкретного случая, подробно описанного в работах [1–6]. В качестве параметров системы установки взяты: модернизированная пушка М-46 (М-47) и простой военный понтон с характеристиками, описанными ниже. В результате используются следующие параметры: Ls = 2,345 м, m = 360 кг, m1 = 50 кг, длина поршня на 0,2 м больше длины канала артиллерийского орудия, L0 = 4 м, La = 3 м, Lb = 1, d = 0,170 м, W0 = 0,001026 м3, ω = 0,3 кг, f = 950000 дж/кг, χ = 1, δ = 1600 кг/м3, p0 = 200000 кг/м2, α = 0,98•10–3 м3/кг, Δ = 293,4 кг/м3, In = = 367000 Па с, θ = 0,2, Q1 = 36000 н, D = 0,168 м, Qp = 250000 н, A = 15 м, B = 3 м, H = 1 м, Il = 0,3, a1 = 3422 Нс2/м2, b1 = 2000000 Н/м2, c1 = 35000 Н/м2.
Для решения задачи воспользуемся численным методом Рунге – Кутты 2-го порядка с шагом t = 10–6. Как показали проведенные численные эксперименты в работах [2–6] – это наиболее оптимальный шаг для получения численных результатов близким с погрешностью до 5 % к практическим результатам. Для проведения численных экспериментов использовано ПО MathCad версия 14, в которое были заложены системы уравнений для 5 этапов извлечения сваи с пограничными условиями и получены численные результаты.
В результате проведенных расчетов, получены следующие значения для соответствующих этапов извлечения сваи для описанных выше параметров:
Первый этап – Ψ0 = 5,86•10–4.
Второй этап – p/t = 0,009 = 1,854•108 Па, v/t = 0,009 = 17,959 м/с, Ψ/t = 0,009 = 0,999, L/t = 0,009 = = 0,091 м, Ln/t = 0,009 = 7,750•10–5 м, V/t = 0,009 = 0,266 м/c.
Третий этап – p/t = 0,032 = 1,6•103 Па, v/t = 0,032 = 0 м/с, L/t = 0,032 = 2,243 м, Ln/t = 0,032 = = 0,246 м, V/t = 0,032 = 0,342 м/c. На этом этапе поршень остановился в артиллерийском орудии, но свая полностью вышла из грунта.
Четвертый этап – L/t = 0,123 = 2,243 м. То есть свая извлечена из грунта полностью, на величину L = 3,243 м.
Пятый этап – максимальная амплитуда колебания системы после выстрела равна y = 0,273 м. Время затухания колебания платформы t = 10,8 сек.
Результат численного эксперимента показывает, что, при описанных технических параметрах, можно извлечь сваю из донного грунта, при определенной подготовке, с одного выстрела. При этом колебания платформы будут быстро затухающими, а амплитуда колебания платформы не превышает 27 % от высоты платформы.
Технические рекомендации
Общие:
Расстояние от дульного среза ствола артиллерийского орудия до поверхности воды должно быть не меньше длины сваи. Для этого в установке необходимо предусмотреть систему подъема артиллерийского орудия или оставлять постоянное положение артиллерийского орудия, но изменять массу заряда, закладываемого в артиллерийское орудие.
Понтон:
Дополнительно были проведены численные эксперименты для еще двух понтонов: армейский нормальный понтон Н2П с техническими характеристика: A = 10,6 м, B = 2,2 м, H = 1,05 м, масса понтона 1900 кг, грузоподъемность 12200 кг; армейский полуторный понтон Н2П с техническими характеристиками: A = 16,06 м, B = 2,2 м, H = 1,05 м, масса понтона 2950 кг, грузоподъемность 18700 кг. Численные эксперименты показали, что использовать такие понтоны возможно, но максимальная амплитуда колебания понтона с артиллерийским орудием будет равна 0,48 м, и при наличии колебаний воды может произойти опрокидывание понтона.
Свая:
Аналогично расчетам для разных типов понтонов были проведены численные эксперименты для нескольких типов свай. В результате сделаны следующие выводы: за один выстрел можно извлечь из донного грунта сваю с диаметром головной части сваи D до D = 0,32 м и длиной L0 = 4 м, величиной начального заглубления до 3 м; с двух выстрелов – с величиной начального заглубления до 5,5 м. Проведены расчеты для существующих свай: С 40-30-3 с размерами 4х0,3х0,3 – возможно извлечь из грунта с одного выстрела, при величине начального заглубления на 3 м; возможно извлечь из грунта с двух выстрелов, при величине начального заглубления на 3,5 и 4 м.
Заключение
В результате полученные результаты расчетов динамики системы «пушка – поршень – свая – понтон – вода – грунт» показывают возможность извлечения сваи из донного грунта с понтона, находящегося на поверхности спокойной воды, с применением откатных артиллерийских орудий. Колебания платформы с артиллерийским орудием при этом после выстрела относительно вертикальной оси небольшие и быстро затухающие.
Библиографическая ссылка
Черников А.В. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДИНАМИКИ УСТАНОВКИ, ИЗВЛЕКАЮЩЕЙ СВАИ ИЗ ДОННОГО ГРУНТА // Современные наукоемкие технологии. – 2018. – № 7. – С. 136-141;URL: https://top-technologies.ru/ru/article/view?id=37093 (дата обращения: 21.11.2024).