Работа посвящена исследованию линейной задачи нестационарной теории внутренних волн, распространяющихся в стратифицированной жидкости.
Задачи о распространении внутренних волн и колебаний в стратифицированных жидкостях представляют собой большой интерес, а исследования в этой области имеют высокое практическое значение, так как позволяют прогнозировать и понимать природу обширного круга явлений, связанных с проблемами океана, физики атмосферы и геофизики.
Стратифицированной называется жидкость, у которой изменение физических свойств в стационарном состоянии происходит лишь в конкретном направлении. То есть функции, определяющие физические характеристики такой жидкости в стационарном состоянии, будут зависеть только от одной пространственной переменной. При этом свойства могут изменяться непрерывно либо скачкообразно.
Будем рассматривать стратификацию жидкости, вызванную силой тяжести. Распределение частиц, солей и взвешенных суспензий, создаваемое в жидкости этой силой, будет сопровождаться неоднородностью плотности жидкости в направлении гравитационного поля.
Постановка задачи
Рассмотрим движение невязкой несжимаемой стратифицированной жидкости, находящейся в состоянии равномерного вращения вокруг вертикальной оси. Введем декартову систему координат (x1, x2, x3), вращающуюся вместе с жидкостью, причем ось Ox3 направим вдоль оси вращения. Относительно этой системы невозмущенная жидкость является покоящейся. Малые движения этой жидкости в поле сил тяжести в отсутствие других внешних сил принято описывать следующей системой уравнений [1]:
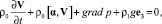 (1.1)
(1.1)
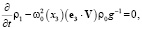 (1.2)
(1.2)
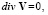 (1.3)
(1.3)
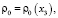 (1.4)
(1.4)
где 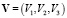 – вектор скорости частиц жидкости;
– вектор скорости частиц жидкости; 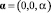 – вектор Кориолиса (α – удвоенная частота вращения); ρ1(x, t) – изменение плотности, вызванное движениями жидкости; р – динамическое давление; e3 – орт оси Ox3; g – ускорение свободного падения. Вектор ge3 представляет из себя вектор ускорения свободного падения, включающий только гравитационную составляющую, тогда как составляющей, вызванной наличием центробежного ускорения, можно пренебречь [1]. Через
– вектор Кориолиса (α – удвоенная частота вращения); ρ1(x, t) – изменение плотности, вызванное движениями жидкости; р – динамическое давление; e3 – орт оси Ox3; g – ускорение свободного падения. Вектор ge3 представляет из себя вектор ускорения свободного падения, включающий только гравитационную составляющую, тогда как составляющей, вызванной наличием центробежного ускорения, можно пренебречь [1]. Через 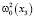 обозначен квадрат частоты Вейсяля – Брента, определяемый формулой
обозначен квадрат частоты Вейсяля – Брента, определяемый формулой
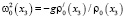 . (2)
. (2)
Частота Вейсяля – Брента ω0(x3) является важнейшей характеристикой динамических свойств стратифицированной жидкости. Предполагается, что распределение плотности жидкости ρ0(x3) удовлетворяет естественному физическому условию устойчивости стратификации: 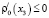 . Стационарная плотность жидкости считается зависящей лишь от переменной x3 [1].
. Стационарная плотность жидкости считается зависящей лишь от переменной x3 [1].
В системе (1) уравнение (1.1) представляет собой закон сохранения импульса; уравнения (1.2) и (1.3) следуют из уравнения неразрывности сплошной среды и предположения о несжимаемости жидкости. Предположение о несжимаемости приводит к уравнению
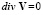 ,
,
а уравнение неразрывности, имеющее в линейном приближении вид
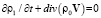 ,
,
будучи переписано в виде
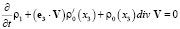 ,
,
с учетом (1.3) приводит к уравнению
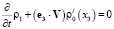 ,
,
которое с учетом представления (2) для частоты Вейсяля – Брента может быть переписано в виде (1.2).
Колебания, описываемые системой (1), которые учитывают силу Кориолиса и гравитационные силы, называются гравитационно-гироскопическими волнами [1–3].
Если рассмотреть явное выражение для частоты Вейсяля – Брента через стационарное распределение плотности (2), то легко видеть, что эта частота будет постоянной в случае, когда функция ρ0(x3) является экспоненциальной, то есть 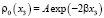 , где A, β – положительные константы. Практическая важность рассмотрения этого случая обусловлена тем, что распределение плотности по экспоненциальному закону является больцмановским распределением в однородном поле сил тяжести и тем самым оказывается одним из наиболее часто встречающихся в физике распределений.
, где A, β – положительные константы. Практическая важность рассмотрения этого случая обусловлена тем, что распределение плотности по экспоненциальному закону является больцмановским распределением в однородном поле сил тяжести и тем самым оказывается одним из наиболее часто встречающихся в физике распределений.
Далее будем изучать систему (1) с учетом экспоненциальной стратификации жидкости и, как следствие, постоянства частоты Вейсяля – Брента:
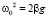 . (3)
. (3)
Будем рассматривать двумерные движения вращающейся стратифицированной жидкости, то есть такие движения, которые описываются функциями V и p, не зависящими от одной из пространственных переменных x1 или x2, например, от переменной x2 [1, 4]. Система (1) для таких движений с учетом (3) примет вид
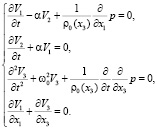 (4)
(4)
Здесь мы уже исключили функцию ρ1.
Из физических и геометрических соображений ясно, что нетривиальные двумерные движения могут происходить лишь в областях типа цилиндров, то есть в областях вида 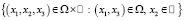 . Здесь
. Здесь 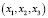 – вращающаяся система координат.
– вращающаяся система координат.
С помощью замены 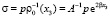 приходим к системе уравнений
приходим к системе уравнений
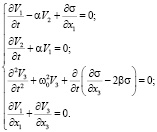 (5)
(5)
Система (4) дополняется следующими начальными и граничными условиями:
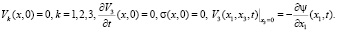 (6)
(6)
Замечание 1. Граничное условие обусловлено существованием функции тока 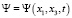 (см., например, [1]), которую можно связать с компонентами вектора скорости частиц следующим соотношением:
(см., например, [1]), которую можно связать с компонентами вектора скорости частиц следующим соотношением: 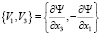 .
.
Предполагается, что функция ψ(x1, t) удовлетворяет следующим условиям:
Условие 1. При некотором δ > 0 равномерно по 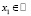 справедлива оценка
справедлива оценка 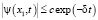 ,
, 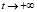 .
.
Условие 2. В 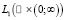 существуют следующие производные функции ψ(x1, t):
существуют следующие производные функции ψ(x1, t): 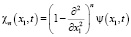 ,
, 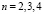 .
.
Условие 3. Имеет место оценка 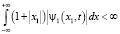 .
.
Условие 4. Функция 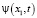 финитна:
финитна: 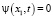 при
при 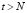 .
.
В работах [5, 6] доказано существование решения задачи (5)–(6) в пространствах интегрируемых функций С.Л. Соболева и выписано два члена асимптотических разложений компонент решения задачи при 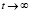 .
.
Явные представления для главных членов асимптотик компонент вектора скорости
В данной статье проводится исследование зависимости главных членов асимптотик компонент вектора скорости 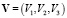 от времени t при разных значениях физических параметров, входящих в систему (5). Непосредственно из работ [5, 6] следует справедливость теоремы о представлениях главных членов асимптотик компонент вектора скорости задачи (5)–(6):
от времени t при разных значениях физических параметров, входящих в систему (5). Непосредственно из работ [5, 6] следует справедливость теоремы о представлениях главных членов асимптотик компонент вектора скорости задачи (5)–(6):
Теорема 1. Пусть выполнены условия 1, 2, 3, 4. Тогда при 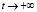 главные члены асимптотик компонент вектора скорости решения задачи (5)–(6) с точностью до постоянного множителя определяются следующими соотношениями:
главные члены асимптотик компонент вектора скорости решения задачи (5)–(6) с точностью до постоянного множителя определяются следующими соотношениями:
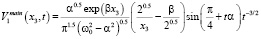 ;
;
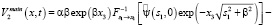
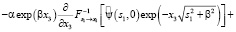
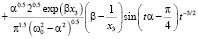 ;
;
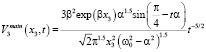 ,
,
где 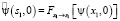 – частичное преобразование Фурье по переменной x1;
– частичное преобразование Фурье по переменной x1; 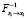 – обратное частичное преобразование Фурье.
– обратное частичное преобразование Фурье.
Заметим, что компонента 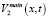 имеет стационарный, не зависящий от времени главный член асимптотики, поэтому для нее приведены два члена асимптотического разложения.
имеет стационарный, не зависящий от времени главный член асимптотики, поэтому для нее приведены два члена асимптотического разложения.
Анализ влияния различных физических параметров на асимптотики компонент вектора скорости
На рис. 1–3 представлены зависимости главных членов асимптотик компонент V1, V3 вектора скорости от времени при различных значениях физических параметров.
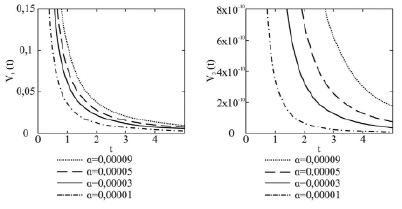
а) б)
Рис. 1. Зависимости главных членов асимптотик (а) компоненты V1, (б) компоненты V3 от времени при различных значениях частоты вращения жидкости α при фиксированных значениях параметра стратификации β и переменной x3
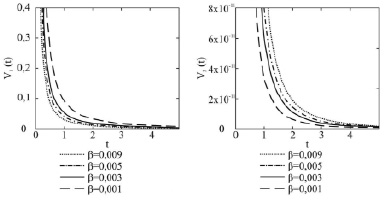
а) б)
Рис. 2. Зависимости главных членов асимптотик (а) компоненты V1, (б) компоненты V3 от времени при различных значениях параметра стратификации β при фиксированных значениях частоты вращения жидкости α и переменной x3
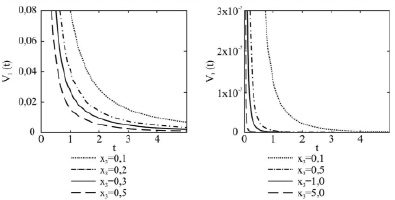
а) б)
Рис. 3. Зависимости главных членов асимптотик (а) компоненты V1, (б) компоненты V3 от времени при различных значениях переменной x3 при фиксированных значениях частоты вращения жидкости α и параметра стратификации β
Выводы
Проведенный анализ позволяет сделать следующие выводы:
1) в рамках рассмотренной модели во всех случаях наблюдается естественное затухание колебаний жидкости с течением времени;
2) увеличение параметра частоты вращения жидкости α приводит к росту значений V1(t), V3(t) при фиксированном времени;
3) увеличение параметра стратификации β приводит к уменьшению значения V1(t) и к увеличению значения V3(t) при фиксированном времени;
4) увеличение параметра x3 приводит к уменьшению значений V1(t), V3(t) при фиксированном времени.
Библиографическая ссылка
Свиридова Е.Н. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ МАЛЫХ ВНУТРЕННИХ ДВИЖЕНИЙ НЕВЯЗКОЙ НЕСЖИМАЕМОЙ СТРАТИФИЦИРОВАННОЙ ЖИДКОСТИ // Современные наукоемкие технологии. 2018. № 7. С. 88-92;URL: https://top-technologies.ru/ru/article/view?id=37084 (дата обращения: 15.02.2026).



