Природно-техногенная безопасность территорий определяется совокупностью факторов окружающей среды и техносферы. Снижение рисков возникновения чрезвычайных ситуаций природного и техногенного характера, как правило, основывается на комплексном мониторинге обстановок (метеорологической, гидрологической, сейсмической, радиационной и т.д.), оперативном контроле состояния объектов окружающей среды и техносферы и адекватной оценке угрозы возникновения опасностей. Для этих целей широко используются методы комплексного оценивания, обеспечивающие формирование обобщенных характеристик [1–4], в условиях консолидации больших объемов данных активно применяется технология хранилищ данных (Data Warehouse) и оперативной аналитической обработки многомерных данных (On-line Analytical Processing, OLAP) [5].
Для комплексного оценивания уровня природно-техногенной безопасности территории в работе [6] предложен подход, обеспечивающий формирование интегральной оценки на основе многомерного аналитического моделирования состояния окружающей среды и объектов техносферы. Данный метод представляет собой развитие метода индексного оценивания уровня благополучия территории [4] за счет включения OLAP-моделей в иерархию формирования комплексного показателя: интегральная оценка формируется на основе многомерных оценок аналитических показателей, которые, в свою очередь, рассчитываются на базе многомерных нормативных значений. Кроме того, характер показателей территориальной безопасности требует повышенной чувствительности оценок к несоответствию показателя установленному нормативу.
Цель исследования: данная работа направлена на обеспечение возможности оценить отклонение значения показателя от интервала нормативных значений с учетом цены делений шкалы аналитического показателя и регулировать скорость изменения оценки при отклонении значений показателя от границ норматива.
Методы исследования: цель исследования достигнута с помощью введения нелинейной модели коэффициента соответствия показателя нормативу. Построение нелинейной модели коэффициента соответствия выполнено на основе адаптации метода формирования функций полезности в задачах многокритериального выбора. Качественное определение формы функции коэффициента соответствия выполнено с помощью неравенства Йенсена.
Результаты исследования и их обсуждение
Согласно предложенному подходу к интегральному аналитическому оцениванию природно-техногенной безопасности территории [6], интегральная оценка комплексного показателя рассчитывается на основе иерархии оценок показателей, формируемых по результатам оперативной аналитической обработки мониторинговых данных.
Количественным выражением уровня безопасности является интегральная оценка комплексного показателя, которая рассчитывается на основе оценок базовых показателей с учетом их значимости в показателе верхнего уровня:
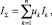 (1)
(1)
где Ik – оценка k-го базового показателя, uk – коэффициент значимости k-го базового показателя. Коэффициент значимости определяется экспертом и представляет собой вес базового показателя.
Оценки базовых показателей представляют собой агрегированные по территории многомерные оценки аналитических показателей, характеризующие природные и техногенные факторы риска возникновения чрезвычайных ситуаций:
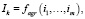 (2)
(2)
где ij, j?{1…m} – многомерная оценка j-го аналитического показателя, fagr – функция агрегирования многомерных оценок аналитического показателя. Функция агрегирования (среднее, минимальное или максимальное значение, среднеквадратичное отклонение, медиана и т.д.) для каждого аналитического показателя задается экспертным путем.
Многомерные оценки аналитических показателей формируются в виде OLAP-моделей и характеризуют соответствие показателя нормативу в разрезе отдельных пунктов наблюдения. Многомерные оценки рассчитываются следующим образом:
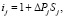 (3)
(3)
где Sj = ±1 – коэффициент, отражающий тенденцию j-го показателя, Sj = 1 – если обстановка улучшается при увеличении значения показателя, Sj = –1 – если обстановка улучшается при уменьшении значения показателя; ΔPj – коэффициент соответствия фактического значения j-го аналитического показателя нормативу. Норматив показателя задается экспертно в виде диапазона значений [Nj; Zj], Nj – минимальное нормативное значение j-го показателя, Zj – максимальное нормативное значение j-го показателя. При этом характер показателей безопасности требует высокой чувствительности оценок к несоответствию показателя установленному нормативу.
В работе [6] для оценки социального благополучия применялась линейная модель расчета коэффициента соответствия показателя Pj нормативу [Nj; Zj]:
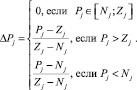 (4)
(4)
Согласно (4) функция коэффициента соответствия монотонно возрастает на всем множестве значений показателя (рис. 1). Коэффициент ΔPj принимает значение равное нулю, когда фактическое значение показателя соответствует нормативу. Если фактическое значение показателя превышает верхнюю границу норматива, коэффициент принимает положительные значения. Если фактическое значение показателя меньше нижней границы норматива, коэффициент принимает отрицательные значения.
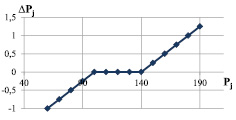
Рис. 1. Линейная модель коэффициента соответствия
Однако такая линейная модель не обеспечивает достаточной чувствительности к отклонению значения показателя от норматива и не позволяет регулировать скорость изменения оценки при отклонении с учетом индивидуальных особенностей показателей. В одних случаях цена делений шкалы показателя уменьшается при удалении значения показателя от границы норматива и, чтобы избежать необоснованно высокой оценки, скорость изменения оценки должна снижаться при увеличении отклонения значения показателя от норматива. В других случаях, наоборот, цена делений шкалы показателя возрастает при удалении значения показателя от границы норматива и, чтобы получить значимую величину оценки при достаточно большом превышении норматива, скорость изменения оценки должна увеличиваться при увеличении отклонения значения показателя от норматива.
Чтобы обеспечить чувствительность оценок к отклонению показателей от норматива и возможность регулировать скорость изменения оценок, в данной работе предлагается нелинейная модель расчета коэффициента соответствия с сохранением монотонности функции
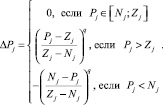 (5)
(5)
Здесь q – коэффициент, характеризующий чувствительность оценки к отклонению показателя от норматива. Значениям q > 1 соответствует выпуклая форма функции (рис. 2), значениям 0 < q < 1 соответствует вогнутая форма функции (рис. 3), значению q = 1 соответствует линейный вид функции. На рис. 2 и 3 показано влияние коэффициента q на изменение значения коэффициента соответствия. С учетом симметричности функции относительно центра интервала [Nj; Zj], на рисунках представлены графики для случаев превышения верхней границы нормативного диапазона.
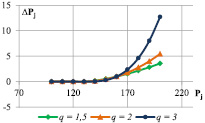
Рис. 2. Семейство выпуклых функций
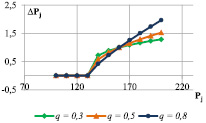
Рис. 3. Семейство вогнутых функций
Построение нелинейной модели коэффициента соответствия выполнено на основе адаптации подхода к построению функций полезности в задачах многокритериального выбора [7, 8]. При оценивании показателей природно-техногенной безопасности территории множество значений каждого показателя разбивается на области так называемых «благоприятных» и «неблагоприятных» значений. Нелинейная модель коэффициента соответствия в области «неблагоприятных» значений строится аналогично нелинейной функции полезности.
Форму функции коэффициента соответствия можно определить с помощью неравенства Йенсена [8]. Для этого рассмотрим функцию на интервале [Pa; Pb], соответствующем длине диапазона нормативных значений и примыкающем к границе нормативного диапазона (рис. 4). Выполнение следующих условий для средней точки интервала Pmid = (Pa + Pb)/2 позволяет определить форму функции коэффициента соответствия ΔP на этом интервале [Pa; Pb]:
1. Если ΔP(Pb) – ΔP(Pmid) = ΔP(Pmid) – ΔP(Pa), то функция линейна.
2. Если ΔP(Pb) – ΔP(Pmid) > ΔP(Pmid) – ΔP(Pa), то функция выпукла.
3. Если ΔP(Pb) – ΔP(Pmid) < ΔP(Pmid) – ΔP(Pa), то функция вогнута.
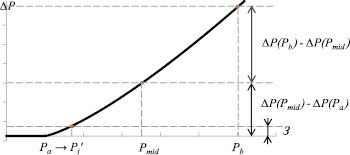
Рис. 4. Определение функции коэффициента соответствия ΔP
Количественно степень кривизны функции можно определить, указав значение показателя Pj, для которого значение коэффициента соответствия ΔP отличается от значения Pa не более чем на малое δ. Тем самым будет получена точка 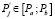 , для которой ΔP = δ. Коэффициент q нелинейной модели рассчитывается по формуле
, для которой ΔP = δ. Коэффициент q нелинейной модели рассчитывается по формуле
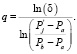 (6)
(6)
В отличие от ранее предложенной линейной модели коэффициента соответствия, рассматриваемая в данной работе нелинейная модель позволяет учитывать ситуации, когда имеет место неравенство цены деления шкалы аналитического показателя, регулировать скорость изменения оценки при отклонении показателя от норматива и с большей точностью оценить соответствие фактического значения показателя нормативу.
В качестве примера рассмотрим показатель гидрологической обстановки «Уровень сбросов гидроэлектростанций» в разрезе Усть-Илимской ГЭС. Нормативные значения уровня сбросов для Усть-Илимской ГЭС заданы интервалом [2200; 2400] куб. м/с.
Для данного показателя экспертным путем установлено, что цена деления шкалы показателя увеличивается при увеличении отклонения значения показателя от норматива. Следовательно, функция коэффициента соответствия имеет выпуклую форму, а скорость прироста коэффициента соответствия увеличивается при увеличении отклонения от норматива в соответствии с величиной коэффициента q. В табл. 1 приведены варианты расчета коэффициента соответствия при различных значениях q.
Таблица 1
Уровень сбросов Усть-Илимской ГЭС
|
№ п/п |
Дата измерения |
Уровень сбросов, куб. м/с |
Отклонение, куб. м/с |
Коэффициент соответствия ΔP |
|||
|
q = 1 |
q = 1,248 |
q = 1,537 |
q = 2,861 |
||||
|
P’ = 5 |
P’ = 10 |
P’ = 40 |
|||||
|
1 |
19.12.2016 |
2190 |
–10 |
–0,05 |
–0,024 |
–0,010 |
–0,00019 |
|
2 |
20.12.2016 |
2180 |
–20 |
–0,10 |
–0,056 |
–0,029 |
–0,0014 |
|
3 |
05.01.2017 |
2100 |
–100 |
–0,50 |
–0,421 |
–0,345 |
–0,138 |
|
4 |
06.01.2017 |
2050 |
–150 |
–0,75 |
–0,698 |
–0,643 |
–0,439 |
|
5 |
09.01.2017 |
1950 |
–250 |
–1,25 |
–1,321 |
–1,409 |
–1,894 |
Значение коэффициента q определяется величиной P', которая принимается экспертом как незначительное отклонение значения показателя от установленного норматива. Так, при P' = 5 куб. м/с коэффициент q = 1,248, при P' = 10 куб. м/с и P' = 40 куб. м/с, коэффициент q равен 1,537 и 2,861 соответственно. В табл. 1 показано отличие нелинейной модели коэффициента соответствия ΔP от линейной, при которой коэффициент q = 1.
В табл. 2 показана зависимость величины многомерной оценки аналитического показателя «Уровень сбросов гидроэлектростанций» в разрезе Усть-Илимской ГЭС от параметров коэффициента соответствия ΔP.
Таблица 2
Оценка уровня сбросов Усть-Илимской ГЭС
|
№ п/п |
Дата измерения |
Уровень воды, куб. м/с |
Отклонение, куб. м/с |
Оценка аналитического показателя i |
|||
|
q = 1 |
q = 1,248 |
q = 1,537 |
q = 2,86 |
||||
|
P’ = 5 |
P’ = 10 |
P’ = 40 |
|||||
|
1 |
19.12.2016 |
2190 |
–10 |
1,05 |
1,024 |
1,01 |
1,00019 |
|
2 |
20.12.2016 |
2180 |
–20 |
1,1 |
1,056 |
1,029 |
1,0014 |
|
3 |
05.01.2017 |
2100 |
–100 |
1,5 |
1,421 |
1,345 |
1,138 |
|
4 |
06.01.2017 |
2050 |
–150 |
1,75 |
1,698 |
1,643 |
1,439 |
|
5 |
09.01.2017 |
1950 |
–250 |
2,25 |
2,321 |
2,409 |
2,894 |
Расчет многомерной оценки аналитического показателя (3) проведен при условии, что обстановка улучшается при уменьшении значения показателя. Также показано различие оценок показателя при использовании линейной и нелинейной модели коэффициента соответствия ΔP.
Рассмотренные примеры наглядно демонстрируют зависимость величины многомерной оценки аналитического показателя от параметров коэффициента соответствия и возможность регулирования чувствительности оценки к отклонению значения показателя от норматива.
Выводы
В работе предложен алгоритм формирования многомерных оценок аналитических показателей природно-техногенной безопасности территории, позволяющий оценить отклонение значений показателя от интервала нормативных значений. С учетом характера аналитических показателей территориальной безопасности предложена нелинейная модель коэффициента соответствия, которая обеспечивает чувствительность оценок к отклонению показателей от норматива и позволяет регулировать скорость изменения оценок на основе анализа цены деления шкалы аналитических показателей. Отличие линейной и нелинейной модели коэффициента соответствия и влияние параметров коэффициента соответствия на величину многомерной оценки наглядно продемонстрировано на примере показателя гидрологического мониторинга.
Библиографическая ссылка
Метус А.М. ФОРМИРОВАНИЕ МНОГОМЕРНОЙ ОЦЕНКИ ПОКАЗАТЕЛЕЙ ПРИРОДНО-ТЕХНОГЕННОЙ БЕЗОПАСНОСТИ ТЕРРИТОРИИ // Современные наукоемкие технологии. 2018. № 7. С. 72-76;URL: https://top-technologies.ru/ru/article/view?id=37081 (дата обращения: 15.02.2026).



