В современных условиях количество данных, на основании которых принимаются важные решения, непрерывно растет, однако увеличение количества данных не сопровождается соответствующим увеличением объема количества полезной информации. Огромные объемы данных часто имеют лишь небольшой информационный контент, а это означает, что высока информационная избыточность. В случае с моделью линейной регрессии мультиколлинеарность можно интерпретировать как тип избыточности. К мультиколлинеарности приводит нарушение одной из предпосылок метода наименьших квадратов (МНК), а именно предпосылки на матрицу регрессоров:
rank(X) = rank(XTX) = k,
где k – число столбцов матрицы регрессоров. Негативные последствия, к которым приводит мультиколлинеарность, хорошо известны [1, 2]. Мультиколлинеарность не только приводит к неустойчивым оценкам регрессионных коэффициентов, но и вызывает некоторые серьезные проблемы в валидации и интерпретации модели.
Существуют различные методы тестирования уровня мультиколлинеарности и ее устранения [1, 3]. Успех методов, используемых для уменьшения или устранения отрицательных эффектов мультиколлинеарности, во многом зависит от степени распознавания мультиколлинеарности. Выбор метода основывается на содержательной постановке задачи и на возможностях используемых компьютерных программ. В задачах, где целью моделирования является выявление раздельного влияния факторов на зависимую переменную, устранение мультиколлинеарности выполняют методами, в основе которых лежит сокращение числа регрессоров. В задачах прогнозирования устранение мультиколлинеарности возможно также за счет их преобразования (компонентный анализ, ридж регрессия).
Материалы и методы исследования
Свободно распространяемая статистическая среда R [4] объединяет язык программирования высокого уровня и библиотеки программных модулей (пакетов) для обработки данных. Постоянно происходит увеличение количества библиотек. Это привело к возникновению распределенной системы хранения и распространения пакетов R, то есть «CRAN» (от «Comprehensive R Archive Network») [5]. Для обнаружения мультиколлинеарности среди регрессоров R-пакеты предоставляют несколько диагностических мер для оценки мультиколлинеарности. В этой работе будет представлен анализ инструментов языка программирования R, направленных на решение проблемы выявления мультиколлинеарности данных. Для сравнительного анализа используются смоделированные данные. Описание данных [1]: «Объем продаж – это зависимая переменная Y (тыс. руб.). В качестве независимых (объясняющих) переменных выбраны: время – X1 (мес.), расходы на рекламу X2 (тыс. руб.), цена товара X3 (руб.), средняя цена товара у конкурентов X4 (руб.), индекс потребительских расходов X5 ( %), количество наблюдений n = 16, количество факторов k = 5».
Результаты исследования и их обсуждение
Выявление мультиколлинеарности с помощью анализа матрицы коэффициентов парной корреляции
Наличие коэффициентов парной корреляции больших |0,8| может свидетельствовать о мультиколлинеарности данных. В среде R построение матрицы коэффициентов парной корреляции выполняется при помощи функции cor(х), применяя которую получаем матрицу коэффициентов парной корреляции (табл. 1). Анализ матрицы коэффициентов парной корреляции показал высокое значение коэффициента корреляции между факторами Х1 и Х5 (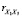 = 0,960), что указывает на наличие мультиколлинеарности.
= 0,960), что указывает на наличие мультиколлинеарности.
Таблица 1
Корреляционная матрица
|
X1 |
X2 |
X3 |
X4 |
X5 |
|
|
X1 |
1,000 |
0,106 |
0,174 |
–0,051 |
0,960 |
|
X2 |
0,106 |
1,000 |
–0,003 |
0,204 |
0,273 |
|
X3 |
0,174 |
–0,003 |
1,000 |
0,698 |
0,235 |
|
X4 |
–0,051 |
0,204 |
0,698 |
1,000 |
0,031 |
|
X5 |
0,960 |
0,273 |
0,235 |
0,031 |
1,000 |
При большом числе регрессоров визуальное исследование корреляционной матрицы становится сложным. В среде R есть возможность облегчить этот процесс с использованием графических функций plotcorr из пакета ellipse и corrplot из одноименного пакета. В пакете ellipse значения коэффициентов корреляции изображены в виде эллипсов. Чем ближе значение коэффициента корреляции к 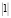 – тем более вытянутым становится эллипс (рис. 1). Наклон эллипса отражает знак.
– тем более вытянутым становится эллипс (рис. 1). Наклон эллипса отражает знак.
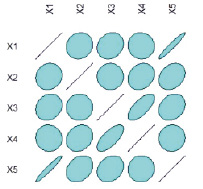
Рис. 1. Изображение матрицы коэффициентов парной корреляции в пакете ellipse
Более информативным представляется применение пакета corrplot, при использовании которого ячейки отображаемой матрицы коэффициентов корреляции залиты цветом в соответствии с уровнем корреляции. Для выявления групп высоко коррелирующих переменных ячейки на таких диаграммах часто упорядочивают в соответствии с результатами параллельно выполняемого кластерного анализа. На рис. 2 выделяются группы тесно связанных факторов: X1, X5 и X3, X4.
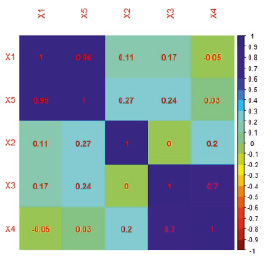
Рис. 2. Матрица коэффициентов парной корреляции в цвете
В состав пакета caret входит функция findCorrelation, которая возвращает вектор с номерами переменных, чей уровень корреляции с другими переменными превышает порог (аргумент cutoff), заданный пользователем и удаляет одну из них.
findCorrelation(R1,cutoff = 0.8,verbose = TRUE,names = TRUE,exact = ncol(R1)< 100)
Compare row 5 and column 1 with corr 0.96
Means: 0.375 vs 0.261 so flagging column 5
All correlations <= 0.8
[1] «X5»
Эту функцию можно рекомендовать для применения только в том случае, когда нет предпочтений по содержательному составу факторов.
Метод дополнительных регрессий. Выявление мультиколлинеарности с помощью исследования факторов инфляции дисперсии
Метод дополнительных регрессий заключается в том, что строятся регрессии для каждого j-го регрессора Xj, (j = 1,…, k, k – число факторов модели), по всем остальным регрессорам, вычисляются коэффициенты детерминации 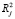 и проверяется их значимость по F-критерию. Если коэффициент детерминации
и проверяется их значимость по F-критерию. Если коэффициент детерминации 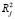 значимо отличается от нуля, то считаем, что фактор Xj приводит к мультиколлинеарности. В R представлен близкий к описанному метод, основанный на вычислении и последующем исследовании так называемого фактора инфляции дисперсии VIF (Variance Inflation Factor).
значимо отличается от нуля, то считаем, что фактор Xj приводит к мультиколлинеарности. В R представлен близкий к описанному метод, основанный на вычислении и последующем исследовании так называемого фактора инфляции дисперсии VIF (Variance Inflation Factor).
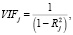
Если 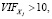 то данный регрессор может привести к мультиколлинеарности.
то данный регрессор может привести к мультиколлинеарности.
В среде R для оценки факторов инфляции дисперсии применяется функция vif(fm,..), где fm – объект, который содержит информацию о построенной модели из пакета car.
fm<-lm(data=tab1,Y~X1+X2+X3+X4+X5 )
vif(fm)
X1 X2 X3 X4 X5
21.112067 1.889292 2.474376 2.331028 23.389356
Анализируя полученные значения факторов инфляции для всех переменных, можно сделать вывод, что факторы X1 и X5 приводят к мультиколлинеарности.
Методов тестирования мультиколлинеарности разработано достаточно много, но нет единого критерия, применяя который можно сделать однозначный вывод о присутствии мультиколлинеарности. Более того, различные методы обнаружения мультиколлинеарности плохо сопоставимы друг с другом. Поэтому в практических задачах применяют несколько методов, полученные результаты обобщаются для получения обоснованного вывода. Например, тест на мультиколлинеарность Фаррара – Глоубера [1] содержит три вида статистических критериев проверки: наличия мультиколлинеарности в общем, критерий («хи-квадрат»); выявление регрессоров, связанных с другими регрессорами (F-критерий); выявление пар тесно связанных переменных (t-тест) дополняют VIF тестом. Хорошо известный метод Бэлсли [6], который реализован в Gretl и называется диагностика Belsley-Kuh-Welsch (BKW) основан на вычислении собственных значений и собственных векторов матрицы. Этот метод позволяет не только выявить мультиколлинеарность среди исходных переменных, но и определить регрессоры, которые показывают: наибольший вклад в зависимости полезно сочетать с VIF тестом и анализом матрицы коэффициентов парной корреляции [7].
Постоянно ведется разработка новых методов исследования мультиколлинеарности. Интересные индикаторы мультиколлинеарности в моделях линейной регрессии представили Д. Курто и Х.К. Пинто [8]. Показатель, который еще не нашел широкого применения, для диагностики мультиколлинеарности с использованием собственных значений или количественной оценки средней корреляции данных «Red Indicator» разработал П. Ковач [9], но этот тест уже включен в рассматриваемый ниже пакет R mctest.
Пакет R mctest для обнаружения мультиколлинеарности
В 2016 г. вышла работа «mctest: пакет R для обнаружения коллинеарности среди регрессоров» [10], а в конце февраля 2018 г. документация пакета была размещена в «CRAN» [11]. В пакете mctest есть две функции: omcdiag и imcdiag, которые обеспечивают общую и индивидуальную диагностическую проверку мультиколлинеарности соответственно, функция mc.plot, которая может использоваться для графического отображения VIF и собственных значений, и функция eigprop. Эта функция вычисляет собственные значения, индексы обусловленности и пропорции дисперсионного разложения коэффициентов регрессии. Фактически в этой функции реализован метод Belsley-Kuh-Welsch [6]. Чтобы проверить линейные зависимости, связанные с соответствующим собственным значением, eigprop сравнивает пропорцию дисперсии с пороговым значением (по умолчанию 0,5) и отображает пропорции, превышающие заданный порог из каждой строки и столбца, если таковые имеются.
Анализ диагностики мультиколлинеарности по методу Белсли с помощью функции eigprop, которой приведен на рис. 3, показал, что наибольшему значению индекса обусловленности (CI) равному 376,49 в шестой строке соответствуют факторы Х1 и Х5, значит, между этими факторами существует тесная зависимость. Заметим, что, по сравнению с предыдущими тестами, появилась новая информация – в 5 строке зафиксирована тесная связь между переменными Х3 и Х4.
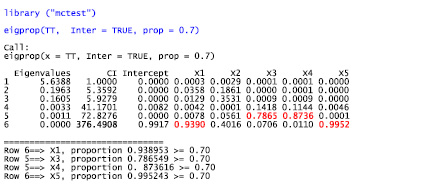
Рис. 3. Результат диагностики коллинеарности по методу Белсли
Выявив с помощью функции eigprop переменные, участвующие в зависимости, удаляют из регрессионной модели одну из этих переменных.
В пакете mctest тесты выявления мультиколлинеарности классифицированы по двум признакам: проверка мультиколлинеарности всего массива данных – общие тесты проверки мультиколлинеарности и выявление регрессоров, приводящих к мультиколлинеарности – индивидуальные тесты.
Общие тесты проверки мультиколлинеарности
Функция omcdiag() реализует общую диагностическую проверку мультиколлинеарности. В эту функцию включены следующие тесты:
- Проверка равенства нулю определителя
Оценки коэффициентов регрессии являются решением системы нормальных уравнений 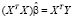 . Если регрессоры мультиколлинеарны, то определитель нормированной корреляционной матрицы
. Если регрессоры мультиколлинеарны, то определитель нормированной корреляционной матрицы 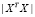 близок к нулю. По умолчанию порог равен 0,1 (detr = 0.01).
близок к нулю. По умолчанию порог равен 0,1 (detr = 0.01).
- Тест Фаррара – Глоубера (1 часть) (При рассмотрении командных кодов функции omcdiag при вычислении статистики Фаррара – Глоубера выявлена допущенная небольшая ошибка)
Проверка наличия мультиколлинеарности всего массива переменных (критерий «хи-квадрат»). Значение статистики Фаррара – Глоубера вычисляется по формуле
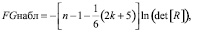
где n – количество наблюдений, k – количество факторов, det[R] – определитель корреляционной матрицы. Эта статистика имеет распределение χ2 (хи-квадрат). Вычисленное значение этого критерия сравнивается с табличным значением χ2 с 0,5k(k – 1) степенями свободы и уровне значимости α. Если FGнабл больше табличного, то считаем, что в массиве объясняющих переменных присутствует мультиколлинеарность.
Red Indicator (Красный индикатор)
Красный индикатор П. Ковача [12] можно использовать для количественной оценки степени избыточности. Определить его можно следующим образом:
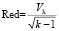 ,
,
где k – количество регрессоров, 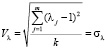 , λj – собственные числа матрицы (XTX). Если значение Красного индикатора равно нулю (Красный = 0), то это свидетельствует об отсутствии избыточности, а значения, близкие к 1 (Красное ~ 1), указывают максимальную избыточность (мультиколлинеарность). По умолчанию порог равен 0,5 (red = 0,5).
, λj – собственные числа матрицы (XTX). Если значение Красного индикатора равно нулю (Красный = 0), то это свидетельствует об отсутствии избыточности, а значения, близкие к 1 (Красное ~ 1), указывают максимальную избыточность (мультиколлинеарность). По умолчанию порог равен 0,5 (red = 0,5).
- Сумма обратных значений собственных чисел
В ортогональной системе 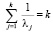 , следовательно, для матрицы корреляции R с собственными числами λj
, следовательно, для матрицы корреляции R с собственными числами λj 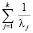 может использоваться для выявления коллинеарности. Если
может использоваться для выявления коллинеарности. Если 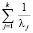 больше, чем число регрессов, используемых в модели, то регрессоры коллинеарны.
больше, чем число регрессов, используемых в модели, то регрессоры коллинеарны.
- Theil индикатор
Theil предложил меру коллинеарности на основе вклада вспомогательных регрессий 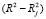 в коэффициент детерминации, где
в коэффициент детерминации, где 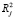 является R2 вспомогательной регрессии.
является R2 вспомогательной регрессии. 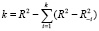 . Если k = 0, то все X взаимно некоррелированы (нет избыточности), если k ~ 1, то коллинеарность существует среди регрессоров. По умолчанию порог равен 0,5 (theil = 0,5).
. Если k = 0, то все X взаимно некоррелированы (нет избыточности), если k ~ 1, то коллинеарность существует среди регрессоров. По умолчанию порог равен 0,5 (theil = 0,5).
- Индекс обусловленности (CI)
Число обусловленности (индекс, параметр обусловленности) CI = cond(XTX) показывает, во сколько раз может возрасти относительная погрешность решения системы нормальных уравнений по сравнению с относительной погрешностью исходных данных. Для симметричной положительно определённой матрицы (XTX) индекс обусловленности равен 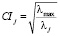 . По умолчанию порог равен 30 (cn = 30).
. По умолчанию порог равен 30 (cn = 30).
Результаты тестирования мультиколлинеарности с помощью функции omcdiag приведены на рис. 4. При заданных пороговых значениях только два теста показали наличие мультиколлинеарности: Фаррара – Глоубера и Sum of Lambda Inverse (сумма обратных значений собственных чисел).
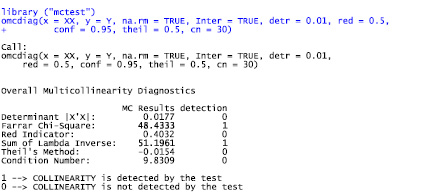
Рис. 4. Результат общей диагностической проверки мультиколлинеарности функции omcdiag в пакете mctest
Диагностические показатели коллинеарности для каждого регрессора
Функция imcdiag() реализует диагностическую проверку мультиколлинеарности, выявляя влияние каждого регрессора. Эта функция включает в себя семь различных тестов.
- VIF тест, который входит также в пакет car;
- тест TOL
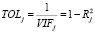 .
.
Если VIF > 10 или значение TOLj ~ 0, то это указывает на существование коллинеарности среди регрессоров.
- Farrar wi (тест Фаррара – Глоубера, 2 часть)
Проверка наличия мультиколлинеарности каждой переменной с другими переменными (F-критерий):
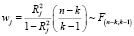 .
.
Если 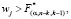 то есть, если вычисленный F-критерий превышает критический
то есть, если вычисленный F-критерий превышает критический 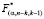 на выбранном уровне значимости, то следует понимать, что конкретный Xj коллинеарен другим регрессорам.
на выбранном уровне значимости, то следует понимать, что конкретный Xj коллинеарен другим регрессорам.
- Fi [13]. Тест практически дублирует предыдущий тест.
Связь F-критерия и R2 модели регрессии Xj на остальные регрессоры может быть использована для обнаружения мультиколлинеарности. Связь описана следующим образом:
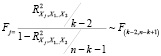 .
.
Если вычисленный F-критерий превышает критический 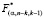 на выбранном уровне значимости, то следует понимать, что конкретный Xj коллинеарен другим регрессорам и и его следует исключить из модели.
на выбранном уровне значимости, то следует понимать, что конкретный Xj коллинеарен другим регрессорам и и его следует исключить из модели.
- Leamer’s test
Лимер [14] предложил меру измерения влияния мультиколлинеарности для j-го регрессора
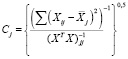 .
.
Если Xj не коррелирует с другими регрессорами, Сj будет равен 1. В противном случае будет равен 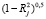 т.е., Сj ~ 0 указывает на существование коллинеарности среди регрессоров.
т.е., Сj ~ 0 указывает на существование коллинеарности среди регрессоров.
- CVIF
Curto и Pinto [15] предложили меру мультиколлинеарности для оценки влияния корреляции между регрессорами в дисперсию
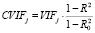 ,
,
где 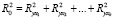 .
.
Если 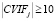 то можно считать, что j-й регрессор приводит к мультиколлинеарности.
то можно считать, что j-й регрессор приводит к мультиколлинеарности.
?- Klein’s rule [16]
Если коэффициент детерминации дополнительной регрессии (регрессии, объясняющей переменной j по всем остальным регрессорам) больше, чем коэффициент детерминации основной регрессии (Y на все регрессоры Х), то мультиколлинеарность можно считать установленной.
На рис. 5 приведены результаты тестирования мультиколлинеарности с помощью функции imcdiag.
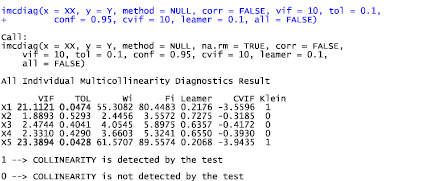
Рис. 5. Результат диагностической проверки индивидуального влияния факторов
Большинство тестов указывают, что Х1 и Х5 являются причиной мультиколлинеарности.
Надо отметить, что в пакете mctest есть функция mctest, в которой реализованы различные режимы, в том числе возможность выполнения функций omcdiag и imcdiag (рис. 6).

Рис. 6. Результат работы функции mctest
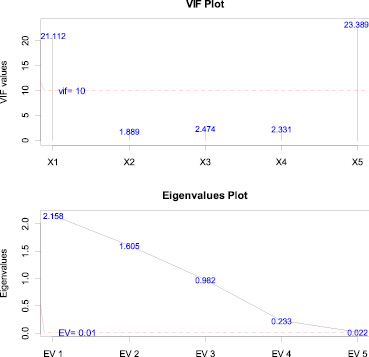
Рис. 7. Графики VIF и собственных значений
Диагностические графики коллинеарности: график VIF и собственных значений
Функция mc.plot может использоваться для отображения графиков значений VIF и собственных значений, по которым можно судить о существовании коллинеарности среди регрессоров. Аргумент vif = 10 и ev = 0,1 являются пороговыми значениями для VIF и собственных значений, соответственно им будет отображаться горизонтальная красная пунктирная линия. Из графика VIF значения VIF каждого регрессора больше 10 указывают на существование мультиколлинеарности среди регрессоров (рис. 7).
Заключение
Для решения проблемы мультиколлинеарности разработано много программных продуктов [17]. В пакете mctest, созданном в среде R, реализована попытка объединить наиболее широко используемые и обсуждаемые диагностики мультиколлинеарности. При реализации допущены ошибки в некоторых тестах (тест Фаррара – Глоубера, Red test) функции omcdiag, дублирование тестов в функции imcdiag. К сожалению, в этом пакете отсутствует тест, основанный на анализе частных коэффициентов корреляции (третий тест Фаррара – Глоубера). При этом необходимо отметить, что функции eigprop, omcdiag и imcdiag облегчают пользователю формирование выводов о существовании мультиколлинеарности среди регрессоров, а также дают представление о том, какой регрессор может быть причиной мультиколлинеарности.
Библиографическая ссылка
Орлова И.В. АНАЛИЗ ИНСТРУМЕНТОВ ЯЗЫКА R ДЛЯ РЕШЕНИЯ ПРОБЛЕМЫ МУЛЬТИКОЛЛИНЕАРНОСТИ ДАННЫХ // Современные наукоемкие технологии. 2018. № 6. С. 129-137;URL: https://top-technologies.ru/ru/article/view?id=37045 (дата обращения: 15.02.2026).
DOI: https://doi.org/10.17513/snt.37045



