Одной из основных задач в производстве дисперсно-армированных бетонов, в том числе и сталефибробетона, является обеспечение равномерности распределения дисперсной арматуры (фибр) в объеме изделия [1, с. 64]. Для неразрушающего контроля равномерности распределения волокон необходима разработка специальных методик и приборов.
Имеются несколько общих способов контроля, основанных на различных физических принципах [2–4]. Во-первых, это просвечивание рентгеновскими лучами, во-вторых, применение ультразвука и, в-третьих, применение электромагнитного поля низкой частоты. Первый способ требует дорогостоящей аппаратуры, повышенных мер безопасности, наличия возможности расположения излучателя и датчиков с обеих сторон конструкции, не применим в бетоне с высоким значением коэффициента армирования. Использование второго способа затруднительно ввиду большого влияния шероховатости поверхности бетона на распространение ультразвука от излучателя к приемникам и сложностей интерпретации сигналов, прошедших через дисперсную арматуру.
Последний способ наиболее удобен для зондирования сталефибробетона, так как стальные фибры обладают большими значениями магнитной проницаемости и проводимости по сравнению с неармированной бетонной матрицей. В работе [5] приведены данные тестирования указанной методики с использованием специальной схемы, моделирующей образец сталефибробетона, установлены зависимости ее электромагнитных характеристик от коэффициента армирования и коэффициента ориентации фибр. Рамки применимости этих результатов ограничены требованием чрезмерной компактности исследуемых экспериментальных образцов.
В работе [6] предложен метод контроля распределения фибр в фибробетоне с применением идеи дифференциального трансформатора, опробованный в условиях опытного производства тонкостенной сталефибробетонной опалубки для ограждающих конструкций помещений электростанций. Разработанный прибор обеспечил уверенную идентификацию параметров фиброзаполнения на глубине до 20 мм в изделии.
Теоретический анализ распределения магнитного поля в материале для данного прибора проведен в [7]. Расчеты подтвердили, что такая схема расположения контуров не позволяет диагностировать распределение фибры на глубине более 20 мм. В настоящей статье автор приводит результаты исследования повышения возможностей диагностики распределения стальных волокон на глубине до 60 мм путем решения задачи управления геометрией расположения электромагнитных контуров измерительной установки.
Изложение и реализация методики
Сталефибробетон считаем средой с однородными магнитными свойствами, усредненными по объему, с характерными линейными размерами, равными (не менее) удвоенному значению длины фибр. В случае расположения фибробетона внутри бесконечно длинного соленоида известно аналитическое выражение для индуктивности элемента этого соленоида [8, с. 24]:
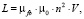 (1)
(1)
где µfb – усредненная величина магнитной проницаемости фибробетона вдоль оси соленоида, µ0 – магнитная постоянная, n – количество витков на единице длины, V – объем элемента соленоида. В первом приближении можно считать, что магнитная проницаемость фибробетона имеет вид
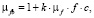 (2)
(2)
где k – коэффициент ориентации волокон вдоль оси соленоида, µf – магнитная проницаемость материала фибр, f – коэффициент армирования (доля объема фибр в бетоне), c – численный коэффициент, учитывающий проводимость фибр, их форму и размер.
При диагностике распределения стальных фибр частота тока должна подбираться таким образом, чтобы уменьшить влияние проводимости фибр на измеряемые параметры контуров. Действительно, эксперименты показали [6], что вплоть до частоты 100 кГц на индуктивность контуров влияет в основном магнитная проницаемость волокон. Поэтому для моделирования трехмерного распределения магнитного поля в сталефибробетоне был применен расчетный блок магнитостатических задач в программном комплексе ANSYS.
Катушка длиной 100 мм квадратного сечения со стороной (внутренняя часть) 50 мм с N = 100 витков немагнитной проволоки диаметром 1 мм с постоянным током силой I = 10А, заполнялась различными комбинациями элементов кубической формы с фибрами (16 элементов с ребром 25 мм). Магнитная проницаемость воздуха 1. Границы области расчета в 500 мм от центра катушки (сфера), граничные условия: тангенциальность магнитного поля. Элементы кубической формы были двух типов. В первом симметрично параллельно расположены 4 стержня квадратного сечения 1 мм2 длиной 20 мм с постоянным изотропным значением магнитной проницаемости µfx = µfy = µfz = 100 (материал элементов немагнитный, µ = 1). Во втором – 9 таких же стержней.
Производился расчет значений магнитной индукции внутри и снаружи катушки, а также значение индуктивности катушки при различных ориентациях фибр. С целью сопоставления были проведены измерения индуктивности катушки с фибробетонными образцами из мелкозернистого бетона размером 40×40×160 мм. Использовались фибры из гладкой низкоуглеродистой стальной проволоки общего назначения длиной 20 мм диаметром 0,35 мм при коэффициенте армирования 0,7, 1,3 и 2,0 %. Фибры подвергались ориентации на стадии формования с помощью магнитного поля, создаваемого этой же катушкой. Коэффициент ориентации подсчитывался после разреза образцов, как отношение среднего количества фибр в сечениях к расчетному значению фибр, находящихся на расстоянии не более половины длины фибры от сечения.
Далее было произведено изменение геометрии расположения тонких катушек, применяемых для диагностики распределения фибр в реальных изделиях, так, чтобы их магнитное поле охватывало более глубокие слои. С этой целью они были разнесены в пространстве, как показано на рис. 1.
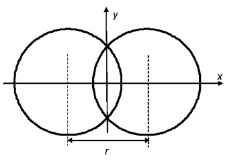
Рис. 1. Расположение катушек для диагностики фибробетона
Катушки располагались горизонтально вплотную друг на друге на поверхности образца толщиной h от 20 до 60 мм (простирающегося до границ расчетной области) с постоянным изотропным значением магнитной проницаемости µfb от 1 до 10. В каждой катушке N = 100 витков немагнитной проволоки диаметром 0,3 мм, радиус катушек R = 50 мм. Сила тока I = 0,1 А. Токи идут по часовой стрелке. Границы области расчета в 1000 мм от начала координат (сфера), граничные условия: вектор индукции касателен к границе. Сходимость решения проверялась сравнением с теоретическими значениями индукции на оси одной тонкой катушки в отсутствии магнетика.
Был произведен расчет значений магнитной индукции во всей области, значений собственных индуктивностей катушек, их взаимной индуктивности и величины магнитного потока через область пересечения катушек.
Результаты исследования и их обсуждение
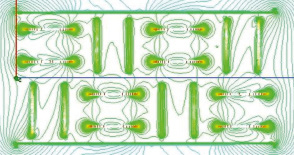
а)
б) в)
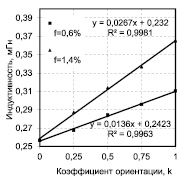
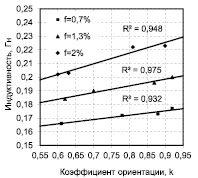
Рис. 2. Катушка индуктивности со сталефибробетоном: а) пример картины изолиний индукции в образце сталефибробетона; б) расчетная индуктивность катушки с образцом сталефибробетона; в) экспериментальные значения индуктивности соленоида
На рис. 2, а, показан пример результата расчета индукции магнитного поля в катушке квадратного сечения со стальными волокнами, расположенными вдоль и поперек продольной оси катушки (показано продольное сечение катушки, проходящее непосредственно через волокна). Данная конфигурация расположения волокон соответствует коэффициенту армирования 0,006 (0,6 % по объему) и коэффициенту ориентации 0,5. Расчет показывает, что индукция магнитного поля значительно увеличивается вблизи поверхности и внутри волокон, имеющих ориентацию в направлении оси катушки. Графики, изображенные на рис. 2, б, подтверждают, что индуктивность катушки с высокой точностью прямо пропорциональна коэффициенту ориентации. Зависимость же индуктивности (а соответственно, и усредненной по объему магнитной проницаемости фибробетона) от коэффициента армирования отклоняется от линейной зависимости на 15 % (следует из сравнения отношений коэффициентов армирования и коэффициентов пропорциональности в аппроксимирующих зависимостях), т.е. наблюдается подобие эффекта насыщения.
На рис. 2, в, показаны экспериментальные зависимости индуктивности катушки (круглого сечения диаметром 800 мм с 2000 витков проволоки) с образцами фибробетона. Данные зависимости с высокой точностью подтверждают расчетные и теоретические результаты.
а) б)
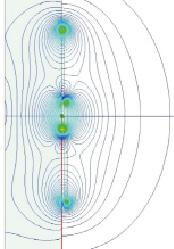
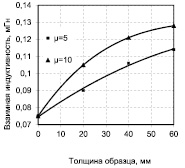
Рис. 3. Магнитное поле двух разнесенных контуров: а) картина изолиний индукции двух контуров (h = 60 мм, r = 70 мм, µfb = 10); б) взаимная индуктивность контуров
На рис. 3, а показан пример расчета индукции магнитного поля, созданного двумя разнесенными контурами, расположенными на поверхности магнитного материала (показан разрез с материалом слева от контуров). Наблюдается изменение изолиний индукции в материале особенно вблизи токов. В области пересечения контуров магнитное поле проникает в материал на глубину с большими значениями индукции до половины толщины образца, далее происходит постепенное выравнивание изолиний. Расчет собственной индуктивности контуров и магнитного потока через область пересечения контуров показал их незначительную зависимость (изменение не более 3 %) от толщины материала в диапазоне от 20 до 60 мм. Взаимная индуктивность, наоборот, показала значительное изменение с увеличением толщины материала (рис. 3, б).
Кроме того, этот параметр сильно зависит от расстояния между катушками (в таблице приведены соответствующие расчетные значения при толщине образца 40 мм). Видно, что наибольшее изменение взаимной индуктивности достигается при расстоянии между центрами катушек (рис. 1) около 70 мм (70 % диаметра катушки).
Взаимная индуктивность при различном расположении контуров
|
Изменяемый параметр |
Взаимная индуктивность, мГн |
|||||
|
Расстояние r, мм |
40 |
50 |
60 |
70 |
80 |
90 |
|
Магнитная проницаемость µfb = 5 |
0,793 |
0,535 |
0,309 |
0,106 |
–0,076 |
–0,231 |
|
Магнитная проницаемость µfb = 10 |
0,871 |
0,59 |
0,343 |
0,121 |
–0,078 |
–0,248 |
|
Изменение индуктивности, % |
9,8 |
10,2 |
11,0 |
14,2 |
2,6 |
7,4 |
Так как взаимная индуктивность при таком расстоянии между катушками принимает минимальные значения, то измерять ее приращение целесообразно по схеме дифференциального трансформатора (рис. 4). При этом идет сравнение сигналов от одинаковых пар катушек – одна пара удалена от магнитных материалов, а вторая находится на поверхности бетона.
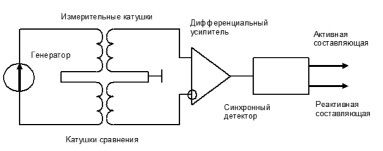
Рис. 4. Приближенная схема детектирования дисперсной арматуры
Для определения коэффициента армирования фибробетона необходимо вначале откалибровать измерительную схему на специально подготовленных образцах. Следует отметить, что достоверные значения коэффициента армирования будут измерены только при равномерном распределении волокон по толщине изделия, в других случаях можно лишь диагностировать степень равномерности их распределения.
Заключение
Значение компонентов усредненной по объему магнитной проницаемости сталефибробетона с равномерным распределением фибры прямо пропорционально коэффициенту ориентации и приближенно пропорционально коэффициенту армирования материала. Это позволяет контролировать содержание фибр путем измерения взаимной индуктивности тонких катушек, расположенных на поверхности изделия.
Для диагностики распределения фибр на глубине до 60 мм рекомендовано разносить центры катушек на расстояние 70 % от их диаметра. Перед измерениями необходимо проведение калибровки на образцах с известным распределением фибр.
Библиографическая ссылка
Матус Е.П. МОДЕЛИРОВАНИЕ И ОБОСНОВАНИЕ МЕТОДИК ИДЕНТИФИКАЦИИ СТРУКТУРЫ ФИБРОБЕТОНА // Современные наукоемкие технологии. 2018. № 6. С. 107-112;URL: https://top-technologies.ru/ru/article/view?id=37041 (дата обращения: 01.02.2026).
DOI: https://doi.org/10.17513/snt.37041



