Волновая передача, изобретенная американским инженером Уолтоном Массером в 1955 г. преимущественно для использования в аэрокосмической промышленности, представляет собой компактный передаточный механизм с высокой степенью редукции [1]. Главными элементами этого механизма в его типовом варианте являются эллиптический генератор волн, гибкое зубчатое колесо и жесткое зубчатое колесо (рис. 1, а). Генератор волн собирается на основе шарикового подшипника, имеющего жесткую внутреннюю дорожку качения эллиптической формы и гибкую тонкостенную наружную дорожку. Гибкое колесо выглядит как закрытый с одного конца гибкий тонкостенный цилиндр, на внешней стороне обода которого выполнен зубчатый венец. Жесткое колесо является толстостенным металлическим кольцом с зубьями по внутреннему диаметру.

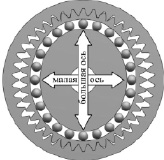
а) б)
Рис. 1. Основные элементы волновой передачи
При работе передачи генератор волн упруго деформирует гибкое колесо вдоль большой оси эллипса. Благодаря этому зубья гибкого колеса входят в зацепление с зубьями жесткого колеса в двух зонах на обоих концах эллиптической оси. При этом вдоль малой оси эллиптически деформированного гибкого колеса зацепление отсутствует (рис. 1, б). При вращении генератора зоны зацепления вращаются вместе с ним. Разница в числе зубьев жесткого и гибкого колеса (обычно равная двум) приводит к относительному движению этих колес таким образом, что после каждого полного оборота генератора гибкое колесо поворачивается относительно жесткого колеса на угол, эквивалентный двум зубьям [2].
По сравнению с классическими зубчатыми передачами волновые передачи имеют множество достоинств, основными из которых являются: возможность передачи больших вращающих моментов, компактность и малый вес, нулевой люфт, высокая степень редукции и высокий КПД. К их недостаткам следует отнести относительно небольшую крутильную жесткость, хотя и малую, но практически не устранимую погрешность позиционирования, возможность возникновения резонансных вибраций, а также нелинейные характеристики жесткости и трения, что затрудняет практическое использование подобных передач [3].
Применение волновых передач в различных практических областях всё более расширяется. В настоящее время они используются в автомобильной и аэрокосмической промышленности, медицинской технике, станко- и роботостроении. Исследования, направленные на совершенствование волновых передач, продолжаются уже много лет и ведутся в различных областях. Одной из таких областей является разработка альтернативных конструкций волновых передач, в которых вместо гибкого зубчатого колеса используются различные варианты роликовой цепи, замкнутой вокруг генератора волн [4–6].
Подобные конструкции выгодно отличаются от классической волновой передачи повышенной нагрузочной способностью и расширенным диапазоном передаточных отношений (за счет смещения его нижней границы) [7]. В то же время они характеризуются усложненной конструкцией, построение которой требует синтеза геометрии передачи для обеспечения надлежащих кинематических связей элементов передачи. В силу сложной кинематики цепной волновой передачи этот синтез может представлять собой серьезную проблему, решение которой связано с необходимостью разработки соответствующей математической модели. Данная модель может быть получена различными путями, однако наиболее эффективным из них представляется использование современных компьютерных CAD и CAE-систем.
Объект и средства моделирования
Иллюстрация названного подхода возможна на примере построения концептуальной модели волновой передачи, использующей в качестве гибкого зубчатого колеса стандартную роликовую цепь. Базовыми компонентами передачи являются жесткое зубчатое колесо, роликовая цепь (состоящая из наружных и внутренних звеньев различной геометрии), ведомый диск, а также входной и выходной валы. Взаимодействие этих компонентов рассматривается на основе их представления в виде многотельной механической системы, под которой понимается набор абсолютно жестких тел, связанных между собой неидеальными шарнирами и согласованно перемещающихся в пространстве под действием внешних и внутренних нагрузок [8]. Их моделирование осуществляется в программной среде автоматизированной системы «Siemens NX» с использованием ее CAD-модуля для твердотельного геометрического моделирования и CAE-модуля для моделирования кинематики и динамики многотельных систем (симуляции движения).
Методика моделирования
Моделирование многотельных систем с использованием современных средств инженерного анализа (CAE-систем) предполагает последовательное выполнение ряда этапов, первым из которых выступает построение сборочной геометрической модели рассматриваемой системы (механизма). Поэтому процесс моделирования в данном случае начинается с формирования сборочной модели волновой передачи, включающей в себя твердотельные параметрические модели всех необходимых компонентов.
Его отправной точкой является подготовка параметрической геометрической модели жесткого зубчатого колеса. В силу специфики предлагаемого варианта волновой передачи зубья этого колеса должны иметь круглый профиль, для определения геометрии которого необходимо и достаточно задать в базе данных модели два параметра. Такими параметрами выступают номинальный шаг цепи P и число зубьев колеса Z. Дальнейшая последовательность моделирования выполнена при использовании шага цепи равного 12,7 мм и четного числа зубьев равного 34 штукам. Ввод значений данных параметров в «Siemens NX» осуществляется при помощи специального диалогового окна «Выражения».
Введенные параметры позволяют определить все основные размеры зубчатого колеса аналитическим либо графическим методом. При этом более простым и удобным в данном случае представляется графический метод. Его реализация предполагает создание эскиза, исходная геометрия которого приведена на рис. 2, и представляет собой набор типовых геометрических примитивов, связанных между собой надлежащими геометрическими и размерными зависимостями. Эти зависимости, корректно наложенные на геометрию эскиза в соответствии с рис. 2, однозначно определяют радиус вершин зубьев Ra и радиус зуба колеса Rr (радиус ролика цепи), которые необходимы для построения других компонентов передачи.
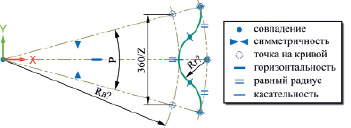
Рис. 2. Построение профиля жесткого зубчатого колеса
Полученные значения указанных размеров в целях удобства их дальнейшего использования сохраняются в соответствующие параметры Ra и Rr. Для этого в «Siemens NX» используется функция определения параметра через интерактивное измерение текущих размеров существующего геометрического элемента, которая доступна в ранее упомянутом окне «Выражения». Для рассматриваемого примера найденные таким способом значения параметров Ra и Rr с учетом округления соответственно составляют 68,821 мм и 3,769 мм.
Далее на основе сгенерированной взаимозависимой геометрии при помощи соответствующих программных инструментов «Siemens NX» формируется полный профиль зубчатого венца в виде непрерывной замкнутой кривой. Данная кривая вместе с добавленной в исходный эскиз окружностью, очерчивающей внешний контур колеса, используется для построения его твердотельной модели с применением операции вытягивания.
На следующем этапе построения сборки формируется геометрическая модель эллиптического кулачка (генератора волн). Для этого, прежде всего, создаются ее параметрические связи с ранее подготовленной моделью зубчатого колеса, т.е. в базе данных модели кулачка объявляются три параметра P, Ra и Rr, значения которых приравниваются к значениям идентичных параметров в модели зубчатого колеса. Данная процедура осуществляется при помощи соответствующих программных инструментов «Siemens NX», доступных в его окне «Выражения». Кроме того, в модель вводится еще один (целочисленный) параметр n, задающий количество роликов в цепи (число зубьев гибкого колеса). В рассматриваемом примере количество роликов принято равным 32 штукам.
Необходимые размеры эллиптического профиля кулачка определяются исходя из следующих условий:
– большая полуось эллипса должна равняться разности радиуса вершин зубьев жесткого колеса (параметр Ra) и радиуса ролика цепи (параметр Rr);
– малая полуось эллипса должна быть такой, чтобы периметр эллипса равнялся периметру окружности, описанной вокруг правильного многоугольника (с числом сторон n), полученного эквидистантным смещением (внутрь) многоугольника с размером стороны равным шагу цепи (параметр P).
Точное аналитическое вычисление размера малой полуоси в программной среде «Siemens NX» представляется чрезвычайно затруднительным, так как связано с необходимостью использования эллиптического интеграла. При этом известные приближенные формулы, как показали предварительные построения, дают существенную погрешность размеров кулачка. По этой причине необходимый эллиптический профиль кулачка также формируется графическим методом.
Для этого строится эскиз, содержащий стандартную эллиптическую кривую, положение и ориентация которой фиксируются путем вспомогательных построений. Большой полуоси эллипса назначается размер равный Ra – Rr, после чего размер малой полуоси находится за счет построения необходимого количества вспомогательных окружностей радиуса Rr, связанных между собой геометрическими и размерными зависимостями и касательных к эллиптической кривой. Примерный вид получаемого таким способом эскиза (для четного числа роликов в цепи) приведен на рис. 3.
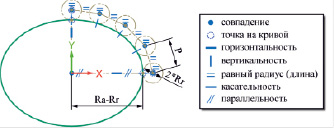
Рис. 3. Построение профиля генератора волн
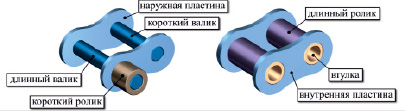
Рис. 4. Модели наружного и внутреннего звеньев цепи
Необходимые размеры малой и большой полуосей эллипса, полученные в результате выполненных построений для рассматриваемого примера, соответственно составляют 56,845 мм и 65,052 мм. После определения размеров эллипса он преобразуется в твердотельную модель кулачка при помощи операции симметричного вытягивания (эскиз остается в плоскости симметрии кулачка). Для своего завершения эта модель дополняется наложенными элементами в виде цилиндрического посадочного отверстия и фасок на эллиптических и круговых кромках, а затем сохраняется в соответствующий файл.
Далее по ходу построения собираются параметрические модели наружного и внутреннего звеньев цепи, служащие сборочными узлами в модели волновой передачи (рис. 4). Здесь в модель наружного звена включаются модели наружной пластины, валиков (длинного и короткого) и короткого ролика, а в модель внутреннего звена – модели внутренней пластины, втулки и длинного ролика. При этом характерные размеры указанных компонентов связываются параметрическими зависимостями с ранее подготовленными деталями передачи.
Передача движения от элементов цепи на выходной вал в рассматриваемом варианте механизма осуществляется через ведомый диск, жестко связанный с выходным валом. Поэтому в качестве следующего компонента сборочной модели волновой передачи формируется геометрическая модель такого диска. Получаемая на данном этапе геометрия диска является предварительной и представляет собой собственно диск с цилиндрическим посадочным отверстием. Это объясняется тем, что окончательная геометрическая конфигурация модели приводного диска синтезируется по результатам расчета на готовой модели движения.
На завершающем этапе подготовки сборочной модели строятся геометрические модели входного и выходного вала, корпуса передачи и крышки этого корпуса. При этом модели валов в данном случае формируются как идентичные друг другу гладкие цилиндры, один из которых (в комплекте с кулачком) будет определять входное звено, а второй (в комплекте с приводным диском) – выходное звено в будущей модели движения. Модели корпуса и крышки, несущие на себе опоры валов, выполняются произвольным образом с учетом возможности обеспечения их геометрической конфигурацией корректного относительного расположения других компонентов.
Полученные геометрические модели компонентов передачи используются для построения ее сборочной модели. Для этого создается файл сборки «Siemens NX» и активируется соответствующая программная среда для работы со сборками, куда последовательно добавляются компоненты модели. При этом необходимое относительное положение компонентов обеспечивается за счет соответствующих зависимостей сборки. Наиболее трудоемкой операцией в данном случае выступает формирование модели цепи, состоящей из отдельных звеньев и замкнутой вокруг эллиптического кулачка.
Завершенная сборочная модель затем преобразуется в модель движения (многотельную систему), для чего активируется один из CAE-модулей «Siemens NX», а именно модуль симуляции движения. Преобразование начинается с ручного определения подвижных и неподвижных звеньев системы (абсолютно жестких тел), в качестве которых рассматриваются компоненты сборки. В единственное неподвижное (заземленное) звено включаются корпус, его крышка и зубчатое колесо. Соответственно, все остальные компоненты модели используются для определения подвижных звеньев в количестве 82 штук. Из них 16 звеньев определяются парой наружных пластин цепи и парой соединяющих их валиков, 16 звеньев – парой внутренних пластин цепи и парой соединяющих их втулок, 48 звеньев – длинными и короткими роликами, 1 звено – кулачком и входным валом и 1 звено – диском и выходным валом. Следует заметить, что в звенья, включающие кулачок и длинные ролики, также включаются эскизы этих деталей (эллиптический и круговой профиль), что требуется для дальнейшего формирования шарниров.
После определения звеньев модели формируются стандартные шарниры между звеньями. В данном случае все стандартные шарниры в модели представлены вращательными шарнирами, которые создаются:
– между парой звеньев, одно из которых включает входной вал, а второе – корпус;
– между парой звеньев, одно из которых включает выходной вал, а второе – крышку корпуса;
– между парами звеньев, одно из которых в каждой паре включает втулку, а второе определяется длинным роликом;
– между парами звеньев, одно из которых в каждой паре включает втулку, а второе – валик;
– между парами звеньев, одно из которых в каждой паре включает длинный валик, а второе определяется коротким роликом.
Итоговое количество вращательных шарниров, сформированных в модели при заданных параметрах, составляет 82 штуки.
Взаимодействие компонентов роликовой цепи с кулачком задается через создание набора нестандартных соединений типа «кривая по кривой», которые представляют собой кинематическую пару, имитирующую кулачковый механизм с роликовым толкателем. При этом в каждой паре для определения направляющей кривой используется эллиптический профиль (исходный эскиз) в средней плоскости кулачка, а для определения перекатываемой кривой – круговой профиль в средней плоскости длинного ролика.
Взаимодействие компонентов цепи с жестким зубчатым колесом обеспечивается за счет создания контактных пар между звеньями, включающими ролики, и звеном, включающим колесо. Непосредственный контакт компонентов цепи с ведомым диском на данном этапе моделирования не определяется.
После создания всех названных соединений производится синтез окончательной геометрии ведомого диска (профилирование пазов под короткие ролики). Для этого, прежде всего, в текущей модели определяются два привода движения: один во вращательном шарнире между входным валом и корпусом и второй во вращательном шарнире между выходным валом и крышкой корпуса. В первом шарнире задается постоянная скорость вращения, определяемая произвольным значением (в рассматриваемом примере 100 об/мин). Во втором шарнире задается скорость вращения, определяемая произведением скорости первого шарнира на номинальное передаточное отношение волновой передачи, вычисляемое через известное число зубьев колеса и число длинных роликов цепи ((32–34)/32). Соответственно, для рассматриваемого примера скорость во втором шарнире составляет минус 6,25 об/мин.
На основе полученной модели, включающей в себя описанные шарниры и приводы, производится расчет кинематики передачи с последующей анимацией его результатов. Очевидно, что в данном случае необходимая геометрия приводного диска будет определяться траекторией движения оси короткого ролика относительно вращающегося диска. Для определения этой траектории в процессе анимации движения осуществляется трассировка центральных точек торцов коротких роликов, обращенных к модели диска. При этом опорным звеном для создания трассировки выступает диск (связанный с выходным валом).
Выполнение трассировки приводит к созданию наборов точек, каждая из которых соответствует положению рассматриваемого ролика относительно диска на данном шаге решения. Пример результатов трассировки для одного из роликов приведен на рис. 5, а. Как видно на приведенном рисунке, геометрическое место полученных точек с большой долей вероятности представляет собой замкнутую эллиптическую кривую.
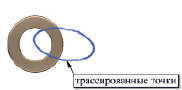
а) б)
Рис. 5. Построение профиля направляющего паза в ведомом диске
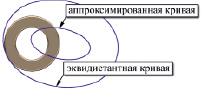
В связи с этим для формирования необходимой траектории к полученным точкам применяется доступная в «Siemens NX» функция построения аппроксимированной кривой с активной опцией «Аппроксимированный эллипс». Для повышения точности аппроксимации все трассированные наборы точек (в количестве 16 штук) предварительно сводятся в один набор путем их последовательного углового переноса в произвольно выбранное фиксированное положение.
Полученная эллиптическая кривая затем используется для построения эквидистантной кривой, размеры которой определяются величиной нормального смещения точек исходной кривой на величину радиуса короткого ролика. Результаты построения аппроксимированной и эквидистантной кривой для рассматриваемого примера приведены на рис. 5, б. Последняя кривая, собственно, и представляет собой искомый профиль паза, за счет которого обеспечивается зацепление элементов цепи с ведомым диском.
Данный профиль далее используется для создания кругового массива сквозных эллиптических отверстий в твердотельной геометрии ведомого диска. После этого геометрия сборочной модели приводится к своему окончательному виду, показанному на рис. 6.
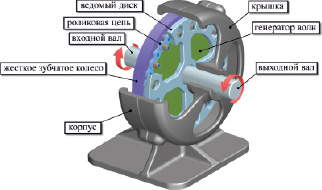
Рис. 6. Сборочная модель цепной волновой передачи
Для оценки разработанной модели на завершающем этапе моделирования производится проверочный расчет, сводящийся к вычислению угловой скорости выходного вала в зависимости от скорости, заданной на входном вале. В процессе его реализации ранее подготовленная модель движения модифицируется следующим образом:
– удаляется ранее созданный привод во вращательном шарнире между выходным валом и корпусом;
– формируются трехмерные контактные пары между ведомым диском и короткими роликами с фактической реализацией контакта по цилиндрическим граням роликов и эллиптическим граням пазов в диске.
Результаты расчета, полученные с использованием модифицированной модели движения, представлены в виде диаграммы на рис. 7.
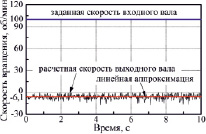
Рис. 7. Изменение скорости вращения входного и выходного валов
Результаты моделирования
На приведенном графике изображено изменение расчетной скорости вращения выходного вала передачи в зависимости от заданной скорости вращения ее входного вала. График показывает, что расчетное значение скорости колеблется около некоторого постоянного значения, что обусловлено особенностями моделирования контактного взаимодействия для отдельных компонентов передачи. Линейная аппроксимация расчетных значений скорости, полученных на каждом шаге решения, позволяет установить величину этого постоянного уровня, равную минус 6,065 об/мин. Следовательно, при номинальной скорости вращения выходного вала, равной 6,25 об/мин, усредненная погрешность расчета составляет около 3 %. Это свидетельствует о корректности разработанной модели и возможности ее использования для расширенного анализа кинематических параметров цепной волновой передачи.
Выводы
Полученные результаты моделирования позволяют сформулировать следующие выводы:
– рассматриваемая концепция цепной волновой передачи характеризуется сложной кинематикой, параметры которой должны обеспечиваться за счет специальной геометрии компонентов передачи;
– параметрическое твердотельное моделирование с использованием CAD-системы позволяет автоматизировать определение основных размеров передачи без проведения трудоемких вычислений и подготовить основу для дальнейшего инженерного анализа;
– симуляция движения передачи с использованием CAE-системы позволяет синтезировать геометрию передачи, форма и размеры которой определяются заданным характером относительного движения компонентов передачи;
– полученная в CAE-системе модель движения, в основе которой лежит понятие многотельной механической системы, позволяет эффективно оценивать кинематические и динамические параметры передачи;
– результаты расчета, полученные с использованием модели движения, могут быть использованы для последующего анализа напряженно-деформированного состояния передачи с использованием метода конечных элементов, например, на основе методик, изложенных в работах [2, 9, 10].
Библиографическая ссылка
Каменев С.В., Марусич К.В. АВТОМАТИЗИРОВАННОЕ МОДЕЛИРОВАНИЕ ЦЕПНОЙ ВОЛНОВОЙ ПЕРЕДАЧИ // Современные наукоемкие технологии. 2018. № 6. С. 88-95;URL: https://top-technologies.ru/ru/article/view?id=37038 (дата обращения: 05.01.2026).
DOI: https://doi.org/10.17513/snt.37038



