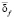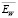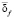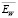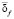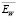Напомним, что качество вейвлет-фильтрации зашумленного сигнала в основном определяется алгоритмами обработки коэффициентов вейвлет-разложения. Большинство применяемых на практике алгоритмов носят пороговый характер: коэффициент разложения меньший по абсолютной величине некоторой пороговой величины зануляется, в противном случае коэффициент сохраняется или подвергается некоторому (в общем случае нелинейному) преобразованию [1–3]. Распространение на практике получили как однопараметрические пороговые функции, зависящие от одного «управляющего» параметра, называемого порогом (например, часто используемые «жесткая» и «мягкая» функции), так и двухпараметрические пороговые функции, в определенной степени свободные от недостатков, присущих однопараметрическим функциям [4].
Опубликованные исследования по выбору вида пороговой функции и величины порога выполнялись при предположении, что шум измерения имеет нормальное распределение. Это предположение является традиционным практически для всех публикаций (как отечественных, так и зарубежных), посвященных пороговым алгоритмам вейвлет-фильтрации. В работе [5] проведены комплексные исследования влияния четырех плотностей распределений (нормальное, равномерное, пуассоновское, импульсное) на ошибку фильтрации одномерных дискретных сигналов при различных уровнях погрешностей измерений. На основе анализа введенного в работе коэффициента эффективности были выбраны оптимальные (по минимуму среднеквадратической ошибки фильтрации) пороговые функции для каждого вида плотности распределения шума измерения. Однако эти результаты были получены на основе вычислительных экспериментов, когда задавался «точный» сигнал, т.е. не искаженный погрешностями измерений. Поэтому открытым остается вопрос: каким образом (или, иначе, каким алгоритмом) выбрать наилучшее значение пороговых величин этих оптимальных пороговых функций? Неудачный выбор величины порога может свести на нет преимущества той или иной пороговой функции. Ответ на этот важный для практики вопрос дается в настоящей работе.
Пороговые алгоритмы вейвлет-фильтрации сигналов
Напомним, что алгоритмы вейвлет-фильтрации основаны на многомасштабном (multiresolution) представлении функции f(x) в базисе вейвлет-функции [1–3]:
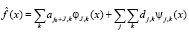 .
.
Функции 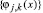 называют масштабирующими (или отцовскими), а функции – вейвлет-функциями (или материнскими). Коэффициенты разложения aj,k называют аппроксимирующими, dj,k – детализирующими, и они определяются выражениями
называют масштабирующими (или отцовскими), а функции – вейвлет-функциями (или материнскими). Коэффициенты разложения aj,k называют аппроксимирующими, dj,k – детализирующими, и они определяются выражениями
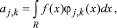
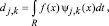
где R – интервал определения функции f(t). Переменная j характеризует уровень разложения, и ее часто называют коэффициентом масштаба, j0 – начальный уровень разложения, J – максимальный уровень разложения, а переменная k – временной сдвиг той или иной базисной функции. Системы функций 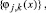
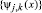 составляют ортогональный базис пространств вейвлет-функций (подробнее см. [1–3]). Обозначим коэффициенты разложения зашумленного сигнала
составляют ортогональный базис пространств вейвлет-функций (подробнее см. [1–3]). Обозначим коэффициенты разложения зашумленного сигнала 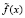 как
как 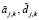 . Заметим, что относительные погрешности аппроксимирующих коэффициентов на порядок и более меньше погрешностей коэффициентов
. Заметим, что относительные погрешности аппроксимирующих коэффициентов на порядок и более меньше погрешностей коэффициентов 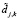 (см. [4]). Поэтому на практике обработке подвергаются только детализирующие коэффициенты
(см. [4]). Поэтому на практике обработке подвергаются только детализирующие коэффициенты 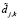 с использованием различных пороговых функций (например, [1, 4, 6]). Суть такой обработки заключается в том, что коэффициенты
с использованием различных пороговых функций (например, [1, 4, 6]). Суть такой обработки заключается в том, что коэффициенты 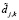 меньшие по модулю задаваемой пороговой величины принимаются равными нулю, в противном случае эти коэффициенты подвергаются преобразованию, чаще всего нелинейному (подробнее см. [7, 8]).
меньшие по модулю задаваемой пороговой величины принимаются равными нулю, в противном случае эти коэффициенты подвергаются преобразованию, чаще всего нелинейному (подробнее см. [7, 8]).
В работе [5] показано, что для рассматриваемых здесь трех распределений погрешностей измерений (нормальное, равномерное, пуассоновское) оптимальной функцией является двухпараметрическая пороговая функция 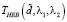 вида
вида
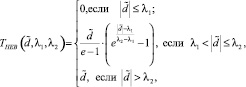 (1)
(1)
зависящая от двух пороговых величин λ1λ2 (имеющая средний коэффициент оптимальности 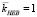 ). Крайне мало этой функции проигрывает (средний коэффициент оптимальности
). Крайне мало этой функции проигрывает (средний коэффициент оптимальности 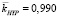 ) однопараметрическая пороговая функция
) однопараметрическая пороговая функция 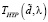 вида
вида
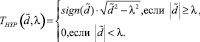 (2)
(2)
Учитывая несущественный проигрыш по коэффициенту оптимальности и тот факт, что оценивание одного оптимального порога существенно проще, чем двух (подробнее см. [4]), в дальнейшем будем рассматривать только функцию (2). На рис. 1 показаны графики функции (1) (сплошная кривая) и функции (2) (точечная кривая), которые хорошо иллюстрируют пороговый характер обработки коэффициентов разложения (λ1 = 1, λ2 = 2). Очевидно, что пороговые величины существенно влияют на точность вейвлет-фильтрации и поэтому перейдем к задаче оценивания оптимального порога λopt для функции (2).
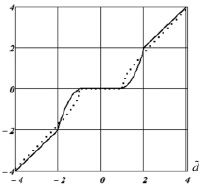
Рис. 1. Графики пороговых функций
Оптимальным порогом будем называть величину λopt, минимизирующую ошибку фильтрации, определяемую выражением
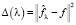 , (3)
, (3)
где 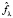 – вектор, составленный из значений отфильтрованного сигнала, f – вектор, составленный из значений точного (не зашумленного сигнала) сигнала,
– вектор, составленный из значений отфильтрованного сигнала, f – вектор, составленный из значений точного (не зашумленного сигнала) сигнала,  – евклидова норма вектора. Вычислить λopt из условия минимума (3) невозможно из-за незнания значений «точного» сигнала (вектор f). Поэтому на практике используют различные алгоритмы выбора λ, позволяющие лучше или хуже оценить λopt. Подробный обзор и сравнения наиболее распространённых на практике алгоритмов выбора для нормального распределения погрешностей измерений приведен в публикациях [4]. Было показано, что наиболее точно оценивает λopt алгоритм, построенный на основе критерия оптимальности. Попробуем использовать этот алгоритм выбора и в случае распределений, отличных от нормального. Кратко изложим сущность этого алгоритма (подробнее см. [4, 9]).
– евклидова норма вектора. Вычислить λopt из условия минимума (3) невозможно из-за незнания значений «точного» сигнала (вектор f). Поэтому на практике используют различные алгоритмы выбора λ, позволяющие лучше или хуже оценить λopt. Подробный обзор и сравнения наиболее распространённых на практике алгоритмов выбора для нормального распределения погрешностей измерений приведен в публикациях [4]. Было показано, что наиболее точно оценивает λopt алгоритм, построенный на основе критерия оптимальности. Попробуем использовать этот алгоритм выбора и в случае распределений, отличных от нормального. Кратко изложим сущность этого алгоритма (подробнее см. [4, 9]).
Для обеспечения асимптотической оптимальности пороговой величины введем на каждом j-м уровне разложения «уровнезависимую» пороговую величину λj в виде
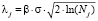 , (4)
, (4)
где Nj – количество обрабатываемых коэффициентов на соответствующем уровне разложения, σ2 – дисперсия погрешностей измерений. На рис. 2 показаны типичные зависимости относительной ошибки фильтрации 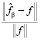 от параметра β для трех распределений (нормальное – сплошная кривая, равномерное – точечная, пуассоновское – штриховая кривая). Видно наличие оптимального значения βopt, которое минимизирует ошибку фильтрации. При этом для каждого распределения погрешностей имеется «свое» значение βopt.
от параметра β для трех распределений (нормальное – сплошная кривая, равномерное – точечная, пуассоновское – штриховая кривая). Видно наличие оптимального значения βopt, которое минимизирует ошибку фильтрации. При этом для каждого распределения погрешностей имеется «свое» значение βopt.
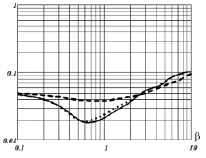
Рис. 2. Зависимость относительной ошибки фильтрации от параметра β
Точное значение βopt невозможно определить из-за незнания «точного» сигнала, и поэтому рассмотрим алгоритм оценивания оптимального коэффициента βopt из условия минимума (3). Определим статистику
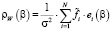 ,
,
где 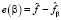 – вектор невязки,
– вектор невязки, 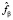 – результат вейвлет-фильтрации с параметром β. В качестве оценки для βopt принимается величина βW для которой выполняется условие
– результат вейвлет-фильтрации с параметром β. В качестве оценки для βopt принимается величина βW для которой выполняется условие
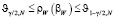 ,
,
где 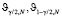 – квантили χ2 – распределения с числом степеней свободы N уровней
– квантили χ2 – распределения с числом степеней свободы N уровней 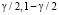 соответственно, N – число значений фильтруемой функции, γ = 0,05 – вероятность ошибки первого рода при проверке статистической гипотезы об оптимальности параметра β (подробнее см. [4, 9]). Подставляя оценку βW в (4), получаем оценку
соответственно, N – число значений фильтруемой функции, γ = 0,05 – вероятность ошибки первого рода при проверке статистической гипотезы об оптимальности параметра β (подробнее см. [4, 9]). Подставляя оценку βW в (4), получаем оценку 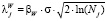 для оптимальной пороговой величины на j-м уровне разложения. Напомним, что ранее исследования такого алгоритма оценивания оптимальных порогов были выполнены только для погрешностей, распределенных по нормальному закону [4, 9].
для оптимальной пороговой величины на j-м уровне разложения. Напомним, что ранее исследования такого алгоритма оценивания оптимальных порогов были выполнены только для погрешностей, распределенных по нормальному закону [4, 9].
Ответим на вопрос о точности оценивания этим алгоритмом оптимальных порогов в случае погрешностей, не подчиняющихся нормальному распределению на основе анализа результатов проведенных вычислительных экспериментов.
Результаты исследования и их обсуждение
В качестве тестового сигнала в вычислительных экспериментах был принят «контрастный» сигнал с резким изменением амплитуд (искаженные значения показаны на рис. 3). Спектр сигнала является широкополосным, что существенно усложняет его фильтрацию из-за совпадений высокочастотных составляющих сигнала и погрешностей измерений. Точные значения (количество отсчетов N = 2048) этого сигнала искажались шумами измерений, имеющими следующие плотности распределений: нормальное распределение; равномерное распределение; пуассоновское распределение. Дисперсии этих распределений определялись таким образом, чтобы обеспечить задаваемый относительный уровень шума, определяемый соотношением 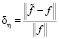 (в экспериментах он был равен 0,05; 0,10; 0,15). На рис. 3, а, показаны значения сигнала, искаженные равномерным шумом, а на рис. 3, б – искажение пуассоновским шумом (относительный уровень шума δη = 0,10).
(в экспериментах он был равен 0,05; 0,10; 0,15). На рис. 3, а, показаны значения сигнала, искаженные равномерным шумом, а на рис. 3, б – искажение пуассоновским шумом (относительный уровень шума δη = 0,10).
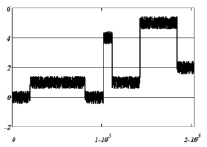
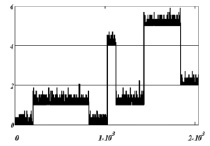
а) б)
Рис. 3. Зашумленные значения тестового сигнала
Далее, в качестве характеристики точности оценивания оптимальной величины βopt введем коэффициент эффективности EW, определяемый соотношением [4]: 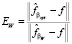 . Очевидно, что 0 < EW ≤ 1 и чем больше EW отклоняется от 1 к нулю, тем больше проигрыш по точности алгоритма вейвлет-фильтрации с параметром βW. Величина EW является случайной величиной – меняется в зависимости от вектора погрешностей η, который искажает точные значения сигнала. Поэтому в качестве неслучайной характеристики берем выборочное среднее значение
. Очевидно, что 0 < EW ≤ 1 и чем больше EW отклоняется от 1 к нулю, тем больше проигрыш по точности алгоритма вейвлет-фильтрации с параметром βW. Величина EW является случайной величиной – меняется в зависимости от вектора погрешностей η, который искажает точные значения сигнала. Поэтому в качестве неслучайной характеристики берем выборочное среднее значение 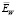 , которое будет вычисляться по выборке
, которое будет вычисляться по выборке 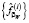 объемом 50, где
объемом 50, где 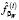 – результат фильтрации l-й реализации зашумленного сигнала.
– результат фильтрации l-й реализации зашумленного сигнала.
В таблице приведены средние значения относительной ошибки фильтрации 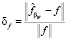 (объем выборки также равен 50) и средние значения коэффициента эффективности
(объем выборки также равен 50) и средние значения коэффициента эффективности 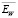 для трех уровней погрешностей, имеющих разные распределения.
для трех уровней погрешностей, имеющих разные распределения.
Средние значения ошибки фильтрации и коэффициента эффективности
|
δη |
Нормальное распределение |
Равномерное распределение |
Распределение Пуассона |
|||
|
|
|
|
|
|
|
|
|
0,05 |
0,020 |
0,982 |
0,019 |
0,984 |
0,038 |
0,996 |
|
0,10 |
0,038 |
0,968 |
0,037 |
0,976 |
0,076 |
0,993 |
|
0,15 |
0,055 |
0,961 |
0,053 |
0,968 |
0,114 |
0,990 |
Выводы
Анализ результатов, приведенных в таблице, позволяет сделать следующие выводы:
1. Алгоритм выбора пороговой величины, основанный на критерии оптимальности, позволяет с приемлемой точностью оценить βopt не только в случае погрешностей, имеющих нормальное распределение, но и в случае фильтрации погрешностей, имеющих равномерное и пуассоновское распределение (высокое значение 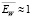 для всех распределений).
для всех распределений).
2. Самая большая ошибка фильтрации наблюдается для пуассоновского распределения погрешностей (как следствие ненулевого математического ожидания погрешностей). Высокие значения коэффициента эффективности 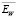 объясняются пологим характером кривой относительной ошибки фильтрации в области ее минимума (см. рис. 2). Поэтому для такого распределения погрешностей применение вейвлет-фильтрации оказывается неэффективным, даже при оптимальных значениях пороговых величин.
объясняются пологим характером кривой относительной ошибки фильтрации в области ее минимума (см. рис. 2). Поэтому для такого распределения погрешностей применение вейвлет-фильтрации оказывается неэффективным, даже при оптимальных значениях пороговых величин.
3. Изложенный подход к выбору пороговой величины достаточно просто реализуется на практике, где в случае неизвестной величины дисперсии σ2 используется ее оценка, приведенная в [4, с. 66].
Библиографическая ссылка
Воскобойников Ю.Е., Крысов Д.А. ВЕЙВЛЕТ-ФИЛЬТРАЦИЯ ШУМОВ РАЗЛИЧНОЙ СТАТИСТИЧЕСКОЙ ПРИРОДЫ // Современные наукоемкие технологии. 2018. № 6. С. 50-54;URL: https://top-technologies.ru/ru/article/view?id=37032 (дата обращения: 13.03.2026).