Наряду со случайной наработкой элемента (системы) до отказа и ее функции распределения, важное значение в теории надежности технических систем имеет функция восстановления (математическое ожидание числа отказов за время от 0 до t). Следует отметить значение функции восстановления при выборе и оптимизации стратегий эксплуатации, где, например, наряду с аварийными восстановлениями проводятся профилактические [1–3].
Простым (обычным) процессом восстановления называется последовательность неотрицательных взаимно независимых случайных величин Xi – наработок элементов от i –1-го до i-го отказа, имеющих одну и ту же функцию распределения F(t) [4, 5].
Функция восстановления H(t) простого процесса восстановления определяется по формуле
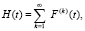(1)
где F(k)(t) – κ-кратная свертка функции распределения F(t):
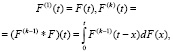
или как решение интегрального уравнения [1, 3, 4]
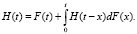(2)
Для многих известных законов распределения наработок элементов технических систем, например экспоненциального, Вейбулла – Гнеденко, Эрланга, нормального, Максвелла и др., функция восстановления получена в явном виде или выписана в виде степенных рядов [1, 4]. Отметим, что плотности распределений этих и многих других известных законов не более чем одномодальны. Это сужает их приложение в решении практических задач надежности технических систем.
Смесь распределений позволяет получать бимодальные (двухвершинные) и даже полимодальные плотности [4].
Интенсивность отказов смеси экспоненциальных распределений имеет период приработочных отказов, и с увеличением продолжительности работы интенсивность становится практически постоянной [6]. Это существенно отличает смесь экспоненциальных распределений от одного экспоненциального распределения. При экспоненциальном распределении интенсивность отказов постоянна – период приработки, так важный и характерный в начальный период работы многих технических систем, отсутствует.
Целью работы является нахождение функций восстановления, когда наработки восстанавливаемых элементов распределены в виде смесей указанных выше законов распределения. Работа представляет собой продолжение исследований, начатых в [4, 6].
Нахождение функций восстановления
Пусть случайные наработки, образующие процесс восстановления, распределены как смесь n функций распределения Fi(t):
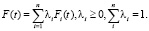
Для этого случая формула (1) принимает вид
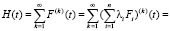
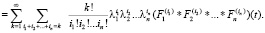
Здесь использована формула
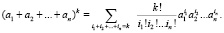
Суммирование ведется по целым неотрицательным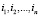 
, таковым, что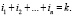 
Функция восстановления при смеси нормальных распределений
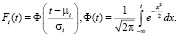
Учитывая, что распределение суммы n независимых случайных величин определяется n-кратной сверткой их функций распределения и что сумма независимых нормально распределенных случайных величин также распределена по нормальному закону, причем математические ожидания и дисперсии суммируются, имеем
.
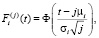
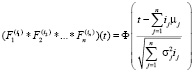Таким образом:
, 
.
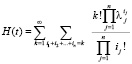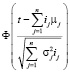Функция восстановления при n = 2 получена в [4]:
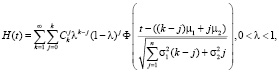
где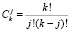 
– количество сочетаний из k элементов по j.
Далее функция восстановления при других законах распределения будет найдена в виде рядов как решение интегрального уравнения (2).
Рассмотрим подробное изложение для случая смеси распределений Вейбулла – Гнеденко. Для других распределений, рассматриваемых в работе, нахождение функции восстановления проводится аналогично.
Функция восстановления при смеси распределений Вейбулла – Гнеденко
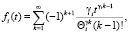
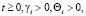
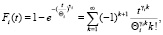
Будем рассматривать случай γi = γ. Имеем
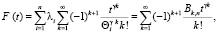(3)
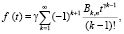
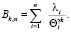
Функцию восстановления находим в виде
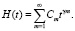(4)
Вычисляем интеграл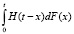 
:
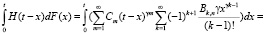
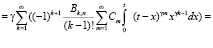
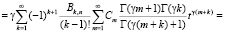
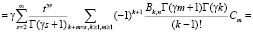
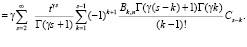(5)
Здесь учтено, что [7]
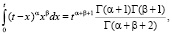
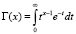– гамма-функция,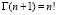 
Следует обратить внимание на возможность обозначить m + k = s, что приводит в (5) только к одной бесконечной сумме по s.
Такая возможность используется для других рассматриваемых в работе законов распределения, образующих смесь.
Подставляем (3), (4), (5) в интегральное уравнение (2):
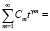
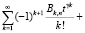
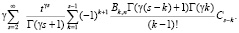(6)
Приравнивая в (6) коэффициенты при одинаковых степенях t, находим Cm:
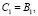
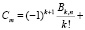
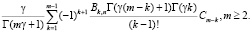
Для случая n = 1 представление функции восстановления в виде ряда получено в [8]. Представление функции восстановления в виде ряда для периодического процесса восстановления k-го порядка при наработках, распределенных по закону Вейбулла – Гнеденко, рассмотрено в [4, 9, 10].
Поступая аналогично нахождению функции восстановления при смеси распределений Вейбулла – Гнеденко, выпишем функции восстановления для ряда смесей распределений, характерных в теории надежности технических систем.
Далее представлены плотности и функции распределения рассматриваемых законов и соответствующих им смесей с полученными представлениями в виде рядов функций восстановления.
Функция восстановления при смеси распределений Эрланга порядка l
.
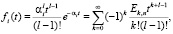
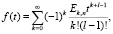
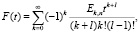
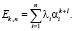
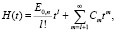
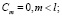
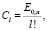
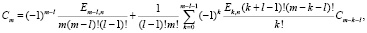
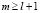Функция восстановления при смеси экспоненциальных распределений
При l = 1 распределение Эрланга является экспоненциальным. Из формул для распределения Эрланга следует
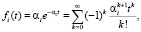
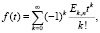
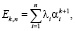
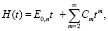
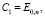
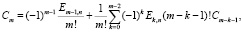
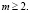
Функция восстановления при смеси распределений Рэлея
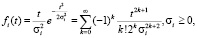
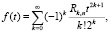
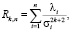
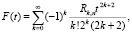
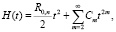
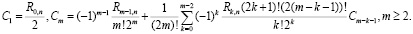
Функция восстановления при смеси распределений Максвелла
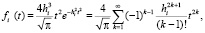
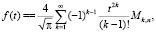
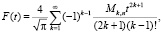
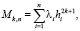
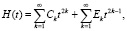
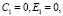
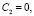
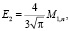
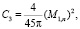
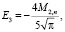
при m ≥ 3:
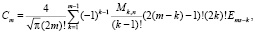
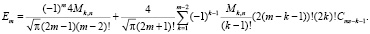
Замечание. Алгоритмы и программы нахождения численных значений параметров, входящих в смесь функций распределения, рассмотрены в работах [4, 11, 12].
Заключение
При решении многих практических задач работы технических систем, у которых отказы имеют случайный характер, важное значение имеет знание функции восстановления – математического ожидания числа отказов за любое время от начала эксплуатации. Например, при выборе стратегий эксплуатации и их оптимизации, когда наряду с аварийными восстановлениями проводятся профилактические.
В теории надежности для классических законов распределения наработок до отказа элементов технических систем функции восстановления известны. Естественно, эти законы не могут охватить разнообразие возможных распределений наработок до отказа в периоде эксплуатации. Например, не более чем одномодальность их плотностей сужает сферу их применения.
Смесь распределений позволяет получать бимодальные (двухвершинные) и даже полимодальные плотности.
Отметим, что знание функции восстановления при простом процессе восстановления позволяет находить функцию восстановления для других моделей процессов восстановления. Например, для общего процесса восстановления, когда функции распределения восстанавливаемых при отказах элементов совпадают, начиная только после первого восстановления.
Пусть F1(t) – функция распределения времени работы элемента до первого отказа, F(t) – функция распределения времени работы восстанавливаемых при отказах элементов после первого отказа. Заметим, что после первого восстановления начинается простой процесс восстановления с функцией распределения F(t).
Если H1(t), H(t) – функции восстановления общего и простого процесса восстановления соответственно, то [1, 4]
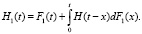
Функции восстановления общего процесса восстановления находятся соответствующим интегрированием функции восстановления простого процесса.
Полученные в работе представления функций восстановления для смесей ряда классических законов распределений наработок, расширяют сферу применения методов теории надежности при решении практических задач эксплуатации технических систем.
Библиографическая ссылка
Вайнштейн В.И. ФУНКЦИИ ВОССТАНОВЛЕНИЯ ПРИ РАСПРЕДЕЛЕНИИ НАРАБОТОК ЭЛЕМЕНТОВ ТЕХНИЧЕСКИХ СИСТЕМ КАК СМЕСЬ N ФУНКЦИЙ РАСПРЕДЕЛЕНИЯ // Современные наукоемкие технологии. – 2018. – № 6. – С. 44-49;URL: https://top-technologies.ru/ru/article/view?id=37031 (дата обращения: 23.11.2024).