Анализ криптографических алгоритмов представляет собой актуальную и востребованную научную работу. Существует множество способов анализа шифров, и одним из них является метод связанных ключей [1]. Метод связанных ключей (МСК) оценивается как эффективный криптографический подход к анализу. В настоящий момент МСК уже успешно опробован на мировых и национальных стандартах шифрования [2–4], но остаётся только теоретической атакой с высоким уровнем допущений относительно знаний аналитика.
Разработчики современных шифров создают сложные процедуры генерации подключей и учитывают МСК. Также они стремятся разрабатывать шифры, которые будут оптимально реализованы на конкретных вычислительных устройствах. Такой двойственный учёт теоретической и практической стороны оправдан и предоставляет высокую степень криптостойкости, но не разрешает все потенциальные проблемы.
По мнению авторов данной статьи, одной из таких проблем может быть использование основ МСК во взаимосвязи с иными видами атак и анализа. Проблема актуальна и для шифра «Кузнечик». Данный алгоритм является современным национальным стандартом РФ в области шифрования. Определение криптостойкости шифра «Кузнечик» является важным процессом, так как стойкость – это основополагающий фактор при выборе алгоритмов шифрования в рамках комплекса мер обеспечения информационной безопасности.
В связи с положениями, описанными выше, было проведено исследование «Кузнечика» с целью определения стойкости шифра относительно МСК с выделением и изучением уникальных свойств и особенностей алгоритма (вырабатывая другие подходы к анализу). В исследовании уровень знания аналитика повышался по необходимости.
Достижением данной работы является выявление параметров восстановления ключа для большего количества раундов (максимально 5 и 6) по сравнению с другими работами в данной тематике [5, 6].
В работе определяется и описывается структура шифра, определяются все необходимые для достижения цели свойства шифра. Далее определяются алгоритмы восстановления промежуточных значений процессов шифрования/дешифрования и описывается алгоритм восстановления ключа.
Структура шифра «Кузнечик»
ГОСТ 34.12-2015 [7] «Кузнечик» является блочным симметричным шифром. Он реализован в соответствии с SP сетью, где процесс дешифрования обратен шифрованию. Вход/выход и промежуточные значения имеют размерность 128 бит, ключ имеет размерность 256 бит. Всего «Кузнечик» состоит из 10 блоков: S и S, p и ?, L и L, R и R, X и l. Где блок X представляет из себя блок побитового сложения двух входных значений по модулю два.
Блоки замены байта p и ? применяются в рамках блоков S и S соответственно и имеют размерность 8 бит. «Кузнечик» имеет предустановленные таблицы замены, которые можно считать массивами с индексами. Выходом блоков p и ? является значение, взятое в таблице замены по индексу равному значению входа.
Блоки замены S и S имеют входную/выходную размерность 128 бит. Входное битовое слово разделяется по 8 бит последовательно непрерывно. Каждый полученный байт заменяется с помощью p и ? блока. Значения после p и ? блоков организуют выходное слово в соответствии с входным порядком битов. Обозначим логическое разбиение 128-битного текста на 16 байт как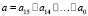 
, 
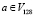. Схематичное представление блоков S и S приведено на рис. 1.
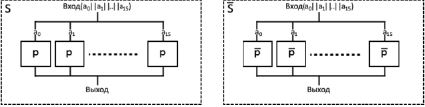
Рис. 1. Схематичное представление блоков S и S, где показан процесс преобразования входного значения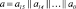 
Блок l имеет размерность входа/выхода 128/8 бит соответственно. Выход генерируется в соответствии с уравнением l(a). Умножение и сложение происходят в поле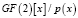 
, где 
.
.
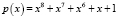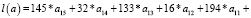
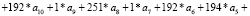
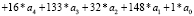Блоки R и R имеют размерность входа/выхода 128 бит. Они используют блок l для вычисления нового старшего байта.
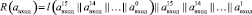
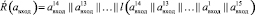
Блоки L и L имеют размерность входа/выхода 128 бит. Они используют R и R соответственно последовательно 16 раз.
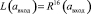
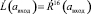
Процессы шифрования и дешифрования отображаются формулами (1, 2) соответственно. Обозначим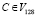 
как закрытый текст и 
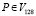как открытый текст.
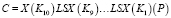, (1)
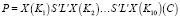. (2)
Ключ шифра имеет размерность 256 бит, а подключ 128 бит. Генерируется 10 подключей для 9 раундов и заключающего X блока. Для выработки подключей используется 32 постоянных продекларированных в стандарте значений Ci. Обозначим старшие 128 бит ключа шифрования как K1, а младшие K2.
,
,
.
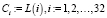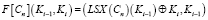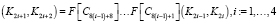Свойства шифра «Кузнечик»
При исследовании структуры шифра на наличие возможных способов применения МСК было установлено, что необходимо анализировать промежуточные дифференциалы процессов шифрования/дешифрования. Промежуточное значение (ПЗ) – это 128-битное слово, которое является результатом вычисления предыдущего блока и входом последующего.
В данном разделе рассматриваются необходимые для МСК дифференциальные свойства (ДС). Дифференциальными свойствами обладает как шифр в общем, так и в частности блоки и их объединения. Шифр имеет 5 основных общих блоков S и S, L и L, X и, следовательно, далее рассматривается их ДС.
Блок X представляет из себя простой и понятный элемент шифра. Он обладает известной структурой, и его свойства соответствуют ДС побитового сложения по модулю два.
Блоки L и L, при рассмотрении с позиции ДС, обладают свойством дистрибутивности. Обозначим значения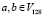 
как входные значения двух процессов преобразования с помощью L и L. Схематично данное ДС изображено на рис. 2.
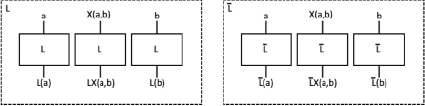
Рис. 2. Схематичное представление ДС блоков L и L, где X(a, b) является дифференциалом входных значений
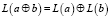
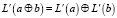
Блоки S и S обладают ДС блоков p и ?. При изучении ДС блоков p и ? было выявлено, что разные дифференциалы входов образуют неодинаковое количество неповторимых выходных дифференциалов. Данное ДС для уникальности обозначим как свойство неравномерности распределения (СНР). Далее рассматривается СНР p блока.
СНР был практически подсчитан и представлен на рис. 3, где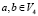 
– это левая и правая часть входного дифференциала соответственно. На данном рисунке значение, соответствующее входному дифференциалу, обозначает количество уникальных выходных дифференциалов, полученных из входного.
Рис. 3. СНР p блока c таблицей замены соответствующей стандарту, где минимальные возможные и невозможные повторения выходного дифференциала обозначаются цветом
Как видно выше, минимальное значение повторений 98, а максимальное 114. Выходные дифференциалы входного дифференциала равного 0 являются уникальными. Выходные дифференциалы di от входного 0x26 образуются в соответствии с формулой
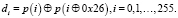(3)
Другим свойством p и ? блоков является неравномерность распределения повторений (СНП). СНП заключается в неравномерности повторений выходных дифференциалов. СПН следует из СНР. Так, известно, что для любого входного дифференциала существует 256 выходных дифференциалов. Если обратить внимание на рис. 3, то становится очевидно, что какие-то уникальные выходные дифференциалы должны повторяться.
Пусть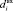 
входной дифференциал р блока, а 
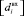список выходных дифференциалов полученных от 
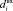по формуле (3). Обозначим 
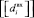как список уникальных значений в списке 
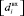. В таком случае СНП можно определить как распределение повторений значений из списка 
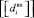в списке 
.
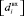В основном СНП полезен для МСК из-за количества повторений в 2 раза. Это наиболее распространённое повторение, так как здесь используются дифференциалы.
Алгоритм восстановления промежуточных значений
Для восстановления ключа шифрования/дешифрования требуется не дифференциал ПЗ, а его значение. Для получения значения ПЗ из его дифференциала был разработан алгоритм восстановления значений ПЗ (АВЗ).
АВЗ основан на СНП блока p, так как он может быть использован при шифровании и дешифровании и позволяет стандартизировать подход к анализу. СНП заключается в p блоке, а данный блок используется в S блоке. Таким образом, АВЗ позволяет восстанавливать значение на входе и выходе S блока. Для применения АВЗ необходим известный дифференциал ПЗ на входе и выходе, разбитые последовательно и непрерывно на байты. Обозначим данные дифференциалы на входе и выходе как Dвх и Dвых соответственно, а их байт как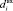 
и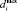 
. Далее следует распределить разбитые байты в соответствии с формулой
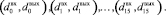(4)
Все полученные пары необходимо соотнести с СНП p блока и получить потенциальные значения пар входов и выходов. Далее следует собрать все пары на входе/выходе и соотнести их соответственно с входом/выходом. В заключение следует скомбинировать все возможные пары значений ПЗ, которые образуют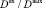 
. Выявлено, что минимально возможно восстановить 216 пар значений ПЗ при использовании АВЗ, а максимально 248.
Алгоритм восстановления ключа
При восстановлении ключей с помощью МСК было установлено, что шифр «Кузнечик» можно представить как криптографический алгоритм с уменьшенным количеством раундов и с нарушенным принципом генерации подключей. Распределим изучаемые представления:
1. Шифр с количеством раундов < 9, выработка подключей нарушено – К1.
2. Шифр с количеством раундов 10, выработка подключей нарушена – К2.
3. Шифр с количеством раундов < 9, стандартная выработка подключей – К3.
4. Шифр с количеством раундов 10, стандартная выработка подключей – К4.
Для всех Кi, i = 1, 2, 3, 4 применяется один и тот же алгоритм. Его реализация требует минимум три процесса дешифрования, где подключи взаимосвязаны. Открытый и закрытый текст известны аналитику. Взаимосвязь подключей известна для пар процессов дешифрования, как отображено на рис. 4.
Рис. 4. Схематичное представление взаимосвязи подключей процессов дешифрования, где каждый процесс дешифрования представлен прямоугольным блоком
Восстановление ключа совершается в два этапа. На первом этапе в соответствии с рис. 4 используется пара (i, i + 1) процессов дешифрования, а на втором (i, i + 2).
Для первого этапа взаимосвязь подключей должна иметь вид, который позволит восстановить дифференциал ПЗ на входе и выходе последнего S блока. Это предоставит условия для применения АВЗ и восстановления возможных первых подключей.
Для второго этапа взаимосвязь подключей должна иметь вид, который позволит восстановить дифференциал ПЗ на входе и выходе предпоследнего S блока. Учитывая знание первого подключа для i-го процесса дешифрования, можно применить АВЗ и восстановить возможные вторые подключи. После восстановления для i-го процесса дешифрования списка возможных первых и вторых подключей, следует их скомбинировать попарно и проверить.
Изучая все представления шифра «Кузнечик» Кi, i = 1, 2, 3, 4, было выявлено, что К1 и К2 идентичны. Для представления К3 были найдены способы применения алгоритма восстановления ключа для пяти и шести подключей с разной сложностью. Представление К4 оказалось абсолютно стойким для МСК в виде, представленном в данной работе. Известно, что К4 соответствует реализации шифра «Кузнечик» по стандарту ГОСТ Р 34.12 – 2015.
Временная сложность и количество восстановленных мастер-ключей разных представлений отображены в таблице. В таблице используются следующие обозначения и сокращения: Мин/Среднее/Макс – это минимальное/среднее/максимальное значение, с – количество восстановленных мастер ключей, символ «–» обозначает неопределённость, t – это количество затрачиваемого времени для вычисления соответствующего количества восстановленных мастер-ключей. Использовался ноутбук HP Pavilion G6, с процессором AMDA10-4600MAPU 2.30 GHz, ОЗУ 8 ГБ и Windows 10x64.
Вычислительная и временная сложность восстановления ключа
|
Представление |
Мин. c |
Макс. c |
Среднее c |
Мин. t |
Среднее t |
|
К1 и К2 |
216 |
296 |
224 |
16 с. |
2 ч. 11 мин. |
|
К3, 5 |
216 |
103*296 |
225 |
16 с. |
1 ч. 33 мин. |
|
К3, 6 |
216 |
2222 |
– |
16 с. |
– |
Результатом работы являются обнаруженные способы применения метода связанных ключей к «Кузнечику», систематизированные дифференциальные свойства блоков шифра, созданные алгоритмы определения значений подключей, а также логические заключения о структурировании и классифицировании подходов к анализу шифра «Кузнечик» с помощью метода связанных ключей.
Библиографическая ссылка
Ищукова Е.А., Красовский А.В., Половко И.Ю. АНАЛИЗ ШИФРА «КУЗНЕЧИК» МЕТОДОМ СВЯЗАННЫХ КЛЮЧЕЙ // Современные наукоемкие технологии. – 2018. – № 5. – С. 85-90;URL: https://top-technologies.ru/ru/article/view?id=36996 (дата обращения: 03.12.2024).