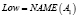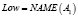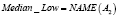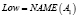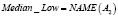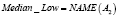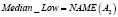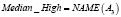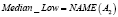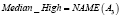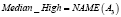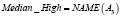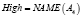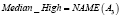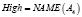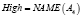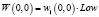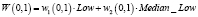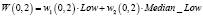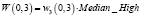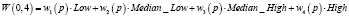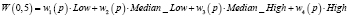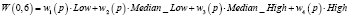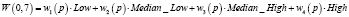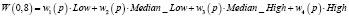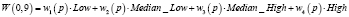Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Бутакова М.А. 1 Климанская Е.В. 1 Чернов А.В. 1

---

1 ФГБОУ ВО «Ростовский государственный университет путей сообщения»

Настоящая статья посвящена исследованию теоретических структур и представлений для нечеткой информационной грануляции. Определена область использования информационной грануляции. Информационная грануляция представляет собой обобщение методов математической кластеризации данных с распространением на данные разнородного вида. Отличием предлагаемых методов информационного гранулирования от ранее известных является их применимость для объединения семантически связанных значений, которые представлены нечеткими значениями. Рассмотрены формальные представления гранулярных вычислений и показана их алгебраическая и геометрическая интерпретация. Дано определение бинарной системы окрестностей. Представлена классификация гранулярных вычислений по ряду признаков. Выполнена формализация представления текста для нечетких элементов управления на основе информационных гранулярных структур. Исследованы как двоичные, так и многозначные гранулярные структуры. Формализовано отношение включения нечеткого покрытия, представление одиночного атрибута с использованием формальных слов. Установлено, что в крупномасштабных вычислениях задачи грануляции можно разделить на три подзадачи: выбор метода формализации грануляции в алгебраической или геометрической постановке, формализация в виде гранулярной структуры, в данном случае в виде двоичного гранулярного представления и применение гранулярных структур к задачам, возникающим в области интеллектуальных систем. Отмечено, что основными приложениями рассматриваемых методов являются интеллектуальный анализ данных и интеллектуальные системы поддержки принятия решений.

Статья в формате PDF

0 KB

гранулярные вычисления

приближенные множества

двоичное отношение

интеллектуальные системы

1. Zadeh L. Towards a theory of fuzzy information granulation and its centrality in human reasoning and fuzzy logic // Fuzzy Sets and Systems. – 1997. – Vol. 1, Iss. 2. – P. 111–127.

2. Lin T.Y. Granular Computing // Rough Sets, Fuzzy Sets, Data Mining, and Granular Computing. LNCS, vol. 2639. Springer, Berlin, Heidelberg. – 2003. – P. 16–24.

3. Pedrycz W. Granular Computing: analysis and design of intelligent systems. – CRC Press, 2013. – 270 p.

4. Бутакова М.А., Иванченко О.В. Гранулярные вычисления как метод обработки нечеткой информации // Труды Ростовского государственного университета путей сообщения. – 2014. – № 4. – С. 9–12.

5. Минаев Ю.Н., Филимонова О.Ю., Минаева Ю.И. Кронекеровы (тензорные) модели нечетко-множественных гранул // Кибернетика и системный анализ. – 2014. – Т. 50, № 4. – С. 42–52.

6. Минаев Ю.Н., Филимонова О.Ю., Минаева Ю.И. Гранулярный компьютинг в системе нечётких множеств на уровне тензорных гранул // Проблемы информатизации и управления. – 2012. – № 4(40). – С. 51–61.

7. Бутакова М.А. Элементы теории гранулярных вычислений с нечеткими приближенными информационными гранулами / М.А. Бутакова, А.Н. Гуда, О.В. Иванченко, Е.В. Карпенко // Вестник РГУПС. – 2015. – № 4(60). – С. 27–33.

8. Бибило П.Н. Логическое проектирование дискретных устройств с использованием продукционно-фреймовой модели представления знаний / П.Н. Бибило, В.И. Романов. – Минск: Беларус. навука, 2011. – 279 с.

Термин «гранулированные вычисления» был впервые использован Л. Заде [1] как название его исследовательской темы в рассуждениях о гранулярной математике: «Информационное гранулирование представляет собой метод объединения массивов данных на основе слияния и разделения по принципу функционального сходства, а также свойства неразличимости этих объектов, основанного на принципе стянутости точек к некоторой центральной точке». Отметим, что «стянутость точек» – это частный случай «центральных точек (объектов)». Л. Заде писал: «Если центральные точки являются целым объектом, то понятия совпадают». Информационное гранулирование, которое формализовано в одной из значимых в данной области работ [2], представляет собой «набор гранул с гранулой, являющейся совокупностью данных (в пространстве данных), которые тянутся к центральному объекту (объектам) (в пространстве объектов) путем неразличимости, сходства или функциональности». Значимыми областями информационного гранулирования [3] являются нечеткие системы [4] и принятие решений в условиях неопределенности [5, 6]. Приложениями информационного гранулирования [7] являются в настоящее время области интеллектуального анализа данных, которые ранее называли методами кластеризации, а также синтез дискретных систем [8]. Отличием кластеризации от гранулирования, по сути, является возможность последнего из методов выполнять объединение схожих по семантике словесных значений на основе неметрических подходов.

Методы исследования

Отличием предлагаемых методов информационного гранулирования от ранее известных является их применимость для объединения семантически связанных значений, которые представлены нечеткими значениями.

Алгебраическая формулировка

Данная формулировка формализуется следующим образом в терминах двух универсальных множеств по принципу «быть объединенным». Пусть P и Q – два объекта, универсальные множества разной природы. Объекты Р и Q могут быть гранулированы, кластеризованы некоторым двоичным отношением, означающим неразличимость, то есть 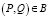. Обратим внимание, что мы не делаем предположения о симметрии, поэтому бинарное отношение имеет смысл направления. В этом случае можно сказать, что Q «стягивается» к P и такой вариант будем называть P центром. Информационная грануляция представляет собой набор 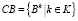, четкого либо нечеткого бинарного отношения B, где K – это набор индексов, который перечисляет неразличимость, сходства или функциональности.

Геометрическая формулировка

Вместо того, чтобы моделировать действие, «будучи объединенным», как в первом случае, рассматриваются последствия гранулирования, другими словами, – «сгущение» объектов, которые связаны с определенным объектом p. Информационная грануляция для p является семейством 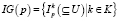вполне определенных, либо размытых подмножеств, которые связаны с p, где K – является мощностью подмножества.

Некоторые отдельные объединяемые объекты можно отнести к одной и той же грануле с разными степенями уверенности. Тем не менее при выполнении информационного гранулирования всегда можно выделить центр информационной гранулы. Как и в других случаях, центр информационной гранулы можно рассматривать с точки зрения различных математических формальных представлений, из которых в данном случае рассмотрим геометрическую формулировку. С данной точки зрения, центр информационной гранулы представляет собой точку, а сама гранула ограничивается в пространстве некоторой окрестностью h. Границы данной окрестности могут определяться, как метрическими, так и неметрическими способами, то есть можно получить либо четкую информационную гранулу (в первом случае), либо нечеткую (во втором случае). Далее, совокупность окрестностей NH(h) можно записать в топологических терминах в виде 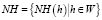, где W – является единичным разбиением множества. Если в каждом разбиении 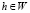имеется не более одной центральной точки, то геометрически это означает существование единственного бинарного отношения в информационном гранулировании. В итоге, имеется бинарная система окрестностей BNH. Таким образом, справедливым является следующее утверждение.

Утверждение. Информационная грануляция CB определяется бинарной системой окрестностей BNH и наоборот, но обратное не единственно, то есть для каждого 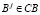имеем

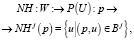
где P(U) является четким / нечетким множеством мощности U.

Можно классифицировать исследуемые структуры исходя из нескольких представлений.

1. Глобальное или локальное гранулирование имеет следующие варианты представления:

a) глобальное гранулирование: грануляция индуцируется бинарными отношениями;

б) локальное гранулирование: грануляция индуцируется системой соседства.

Примером глобального гранулирования является, например, вложение окрестностей топологических пространств, а примером локального гранулирования является уточнение границ окрестностей топологического подмножества. Заметим, что локальное информационное гранулирование индуцируется окрестностью системы пространств с получением конечных гранул в каждой точке пространства. Эти два вида гранулирования неэквивалентны (см. утверждение 1).

2. Одиночное, множественное, вложенное гранулирование можно разделить:

а) на гранулирование в одном уровне, то есть двоичное гранулирование, при котором процесс индуцируется бинарной системой окрестностей или бинарным отношением, которые, естественно, эквивалентны;

б) конечное или многократное гранулирование, при котором глобальное гранулирование индуцируется конечным множеством бинарных отношений;

в) сильно / слабо вложенные уровни гранулирования, при котором каждое локальное гранулирование индуцируется конечным семейством сильно / слабо вложенных бинарных систем окрестностей грануляции.

Обозначенная сильно вложенная грануляция означает, что каждая гранула на некотором уровне j является объединением некоторых гранул на следующем уровне 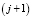. Сильная вложенность автоматически проявляется при условии, что гранулы являются разделяющими. Ярким примером сильно вложенной грануляции является иерархическая структура. Вложенность без таких ограничений называется слабой вложенностью.

Открытое и закрытое гранулирование разделяется:

а) на случай гранулирования с совпадением пространств данных и объекта, когда существует единственная метрика для установления степени сходства / различения;

б) случай гранулирования с различными пространствами данных и объекта, а следовательно, возможности существования различных метрик, определяющих неразличимость объектов.

Двоичная гранулярная структура и однозначные представления

В этом подразделе мы будем предполагать, что NH индуцируется конечным набором B бинарных отношений (или двоичных систем окрестностей).

По аналогии с работой [2] выполним формализацию информационной гранулы в виде гранулированных структур двух видов: 1) 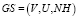и 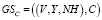, где V – пространство объекта, U – пространство данных или информационное пространство (V и U может быть одним и тем же множеством), NH – многократное гранулирование (геометрически, оно – система окрестностей), а С – пространство понятий, состоящее из всех содержательных названий гранул.

Кортеж ((V, U, B), C) = (V, U, B, C) будем называть двоичным гранулярным представлением структуры (ДГПС). Когда V является конечным, ДГПС может принимать формат таблицы. В этом случае ДГПС эквивалентно таблице двоичной информации. Это можно проиллюстрировать данными из табл. 1. В ней карта, обозначенная «>», является однозначной, и, следовательно, составив карту именования, мы имеем однозначное представление. Обратим внимание, что бинарные окрестности как перекрываются. Они должны дать возможность многозначного представления информационного гранулирования.

Таблица 1

Карты именования

Примечание. «>» Представляет собой двоичную систему окрестности (двоичные отношения).

Если U = V, а B – семейство разбиений, то кортеж (V, U, B, C) становится тройным кортежем (V, B, C) и называется грубой структурой представления. Тогда, если V является конечным, оно принимает табличный формат и эквивалентно информации табл. 1. При использовании битов для представления гранул, как классов эквивалентности подмножеств V, грубая структура представления является обобщением концепции базы данных с растровыми индексами.

Существенным неметрическим способом информационного гранулирования является разбиение по индукции. В нем бинарное отношение (или двоичная система окрестностей):

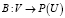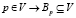; индуцирует разбиение 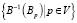; будем называть это индуцированным разбиением (отношением эквивалентности) B и обозначать через EB.

Класс эквивалентности, 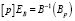, или просто [p], называется центром Bp. Центр [p] состоит из всех тех точек, которые отображаются во множество 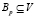, (см. табл. 1).

Применение ДГПС к интеллектуальным системам

Далее рассмотрим некоторые важные приложения ДГПС. Среди таких приложений можно выделить: нечетко-лингвистическое представление элементов управления; приближенный лингвистический поиск; системы классификации слабоструктурированных данных; интеллектуальные системы принятия групповых решений на основе недостаточно определенной информации и другие.

Например, для нечетко-лингвистического представления элементов управления можно использовать многозначные представления ДГПС, где каждому объекту сопоставлено несколько гранул. Однако в нечетких системах можно сформировать «взвешенное среднее представление», поэтому в приведенном в табл. 2 примере оценки являются однозначными.

Таблица 2

Оценки функций включения нечеткого покрытия

Примером использования вышеизложенных структур для приближенного лингвистического поиска являются векторнозначные представления ДГПС. Определив гранулы, как нечеткие множества, например, A1(p), A2(p), A3(p), A4(p), получается векторнозначное представление ДГПС. Однако и в данном случае можно вычислить «средневзвешенное» значение и получить одно инфогранулярное представление. Рассмотрим, например, следующие формальные выражения:

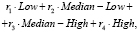
где r1, r2, r3, r4 – действительные числа.

Получаем следующую таблицу (табл. 3) по примеру работы [2].

Математически совокупность всех таких выражений образует абстрактное векторное пространство над действительными числами. Обозначим векторное пространство FW(U). Каждый вектор является формальным словом. Пусть wi(p) представляет класс Ai в p, т.е. 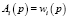. Будем называть wi(p) весом p в Ai. Основываясь на весе wi(p) и многозначном табличном представлении (табл. 2, 3), мы сформируем FW-представление, формальное слово, представленное следующим образом: 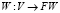; 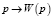, определяемое как 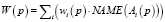. Что касается данного примера, имеем формальное слово представления p:

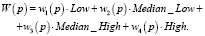
Таблица 4

Представление одиночного атрибута с использованием формальных слов

Табл. 4, которая получена по результатам работы [2], состоит из всех таких формальных выражений. В ней представлены одиночные атрибуты с использованием формальных слов.

Выводы

Гранулированные вычисления являются перспективной методологией вычислений. В крупномасштабных вычислениях решение поставленной задачи состоит из трех этапов: 1) выбор метода формализации грануляции в алгебраической или геометрической постановке; 2) формализация в виде гранулярной структуры, в данном случае в виде двоичного гранулярного представления и 3) применение гранулярных структур к задачам, возникающим в области интеллектуальных систем. На первом этапе весьма важным является выбор либо алгебраического, то есть теоретико-множественного подхода к грануляции, либо геометрической, то есть пространственной интерпретации грануляции. На втором этапе одним из достаточно простых естественных универсальных представлений можно выбрать ДГПС представление, дающее возможность на следующем этапе применить эту структуру в виде табличного представления данных в интеллектуальных системах.

Работа выполнена при финансовой поддержке РФФИ, проекты 18-01-00402-а, 18-08-00549-а, 17-07-00620-a, 16-07-00888-а, 16-01-00597-a.

Библиографическая ссылка