Ранее автором в [1] был рассмотрен химико-технологический процесс (ХТП) сушки движущейся на конвейере сложной многостадийной химико-технологической системы (ХТС) обжиговой машины многослойной массы окатышей, широко применяемый в химической и металлургической промышленности при термической обработке окомкованного минерального сырья [2]. Анализ полученных в результате оптимизации энергоресурсоэффективности динамического многостадийного ХТП сушки фосфоритовых окатышей в движущейся плотной многослойной массе показал, что существенную роль оказывает стационарная, в рамках отдельно взятой вакуум-камеры обжиговой машины ХТС, условная оптимизация энергоресурсоэффективности ХТП статической сушки многослойной массы фосфоритовых окатышей [3].
Технологический режим стационарного ХТП сушки многослойной массы фосфоритовых окатышей определяется: температурой газа-теплоносителя Тg0 и скоростью его подачи Wg. Качество и завершённость ХТП сушки характеризуются: тепловыми параметрами – температура окатышей Tm(x, y), зависящая от координаты x по радиусу окатыша и координаты y высоты в вертикальной многослойной укладке окатышей, градиент температуры ∂Tm/∂x, скорость нагрева ∂Tm/∂τ, температура газа на выходе из многослойной укладки окатышей Tgh и параметрами состояния – влагосодержание u(y), интенсивность влагопереноса I(x, y), относительная степень высушивания ψ(y) [4].
В результате дискретизации по времени стадий прохождения отдельных вакуум-камер на конвейерах обжиговых машин в ХТС, для которых формируются различные векторы управляющих параметров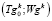 
.
В результате такой декомпозиции для каждой вакуум-камеры можно выделить следующие наборы управляющих параметров:
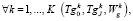
где K – число вакуум-камер конвейера обжиговой машины, соответствующих стадиям процесса сушки окатышей;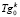 
– температура газа-теплоносителя на входе в слой; 
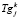– температура газа-теплоносителя после прохождения j элементарных слоёв высотой Δy, в k-й вакуум-камере; 
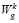– скорость движения газа теплоносителя в k-й вакуум-камере [5].
Себестоимость готовых окатышей формируется в основном за счет удельного расхода электрической Qэл и тепловой Qтеп энергии. Оптимальным считается технологический режим, при котором необходимое качество готового продукта, определяемое завершенностью процесса сушки, достигается при минимуме стоимости израсходованной тепловой и электрической энергии, причем учитывается, что стоимость электрической энергии Pэл дороже тепловой Pтеп. Содержательная постановка задачи построения процедуры условной оптимизации формулируется так: найти такое значение вектора управляющих параметров (Тg0, Wg), чтобы значения U и P = PэлQэл + PтепQтеп достигали своего наименьшего значения. В силу технических особенностей обжиговой машины на вектор управляющих параметров накладываются ограничения: скорость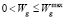 
и температуру 
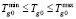газа-теплоносителя на входе в слой, а также на вектор параметров состояния локализованного ХЭТП сушки (Tm, ∂Tm/∂x, ∂Tm/∂τ, Tgh, U, I, ψ) – температуру газа-теплоносителя на выходе 
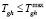, скорость нагрева 
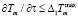и градиент 
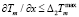температуры в окатыше, влагосодержание U ≤ Umax и интенсивность влагопереноса I ≤ Imax.
В качестве критерия энергоресурсоэффективности локального ХТП сушки многослойной укладки авторами рассматривалось выражение
F(Тg0, Wg) = α1U(Тg0, Wg) + α2P(Тg0, Wg), (1)
где коэффициенты α1 и α2 обеспечивают ранжированность критериев в двухкритериальной задаче оптимизации [6, 7].
Математическое описание ХТП сушки движущейся многослойной массы фосфоритовых окатышей, представляется в виде системы дифференциальных уравнений в частных производных (ДУЧП), решение которой возможно лишь численными методами по разработанной автором компьютерной программе [1].
Содержательная постановка задачи условной оптимизации энергоресурсоэффективности локализованного ХТП сушки многослойной массы фосфоритовых окатышей заключается в поиске экстремума критерия F (целевой функции), определяемом формулой (1), при заданных ограничениях в виде неравенств, т.е. в решении задачи математического нелинейного программирования [8, 9].
Для решения поставленной задачи условной оптимизации потребовалось применение, поисковых методов, в которых направление минимизации определяется на основании последовательных вычислений критерия F, и они не требуют регулярности и дифференцируемости целевой функции F. На практике поисковые алгоритмы оказываются достаточно эффективными и удобными, особенно при реализации решения на ЭВМ.
Исключительно эффективным при решении поисковых задач безусловной оптимизации является предложенный Нелдером и Мидом [8] метод деформируемого многогранника. В нем целевая функция от двумерного вектора F(Тg0, Wg) минимизируется с помощью деформации специально подобранного симплекса. Вершина симплекса, в которой значение F максимально, проецируется через центр тяжести оставшихся вершин. Улучшение значений F производится с помощью последовательной замены точки с максимальным значением F на лучшие с помощью поиска вдоль проецирующей линии, в соответствии с разработанной авторами процедурой. Деформируемый от итерации к итерации многогранник (симплекс) в процессе поиска адаптируется к поведению целевой функции F, вытягиваясь вдоль длинных склонов, изменяя направление в изогнутых впадинах и сжимаясь в окрестности минимума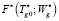 
. Процедура безусловной оптимизации, используя априорные знания о характере критерия энергоресурсоэффективности F, позволяет модифицировать метод деформируемого многогранника и ускорить нахождение экстремума.
Выполнение ограничений на управляющие параметры – скорость подачи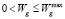 
и температуру 
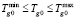газа-теплоносителя на входе в локализованную многослойную укладку окатышей достигается введением в критерий F барьерных функций вида
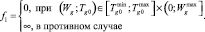
Это ограничение является наиболее жестким, ибо оно обеспечивает математически-корректное и физически-осуществимое решение системы ДУЧП представленной в [1].
Выполнение остальных условий осуществляется методом штрафных функций типа «квадрата срезки» с введением вспомогательного аргумента γi, обеспечивающего одинаковый порядок величин входящих в систему ограничений:
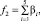
где
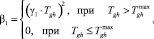
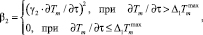
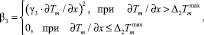
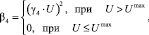
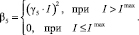
Для увеличения скорости нахождения минимума на каждой стадии дискретизации по времени прохождения отдельных вакуум-камер на конвейерах обжиговых машин, для которых формируются различные векторы управляющих параметров, на каждой последующей стадии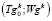 
, в качестве начальной точки поиска экстремума критерия 
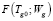берётся найденная точка минимума 
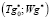на предыдущей стадии дискретизации по времени 
.
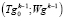Разработанная авторами процедура условной оптимизации критерия энергоресурсоэффективности методами нелинейного программирования и оптимизации реализована в комплексах программ, написанных на языке Borland C++. Проводились многочисленные компьютерные вычислительные эксперименты по оптимизации энергоресурсоэффективности для локальных стадий ХТП многослойной сушки фосфоритовых окатышей в обжиговой конвейерной машине ОК-520Ф, в которой предусмотрено 11 вакуум-камер k = 11 [10].
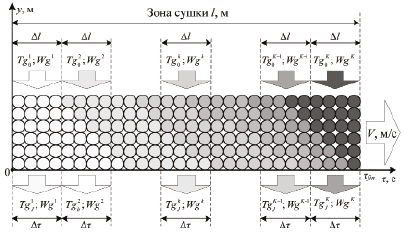
Рис. 1. Проиллюстрирована декомпозиция ХЭТП сушки движущейся многослойной массы фосфоритовых окатышей при дискретизации по времени
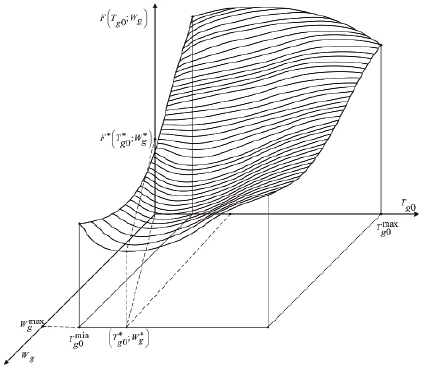
Рис. 2. Результат реализации процедуры условной оптимизации критерия энергоресурсоэффективности для локальной стадии ХЭТП сушки, четвёртой вакуум-камеры k = 4. Здесь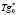 
= 478 K, Wg* = 1,3 м/с
На рис. 2 представлен результат вычислительного эксперимента реализации процедуры условной оптимизации критерия энергоресурсоэффективности для локальной стадии ХТП сушки многослойной массы фосфоритовых окатышей, четвёртой вакуум-камеры k = 4.
В полученном оптимальном режиме сушки скорость газа-теплоносителя максимально возможная Wg* = 1,3 м/с. Температура подачи газа-теплоносителя составляет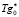 
= 478 К. Расчёты проводились при следующих граничных значениях параметров ХТП многослойной сушки фосфоритовых окатышей в сложной ХТС обжиговой конвейерной машине: 
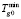= 290 К, 
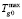= 1673 К, 
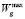= 1,3 м/с, Imax = 3 кг/(м2·с)·103, Umax = 11 %, 
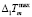=10 К/с, 
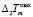= 5·10-3К/м.
Такой подход к определению экстремума критерия энергоресурсоэффективности многостадийного химико-энерготехнологического процесса сушки многослойной массы фосфоритовых окатышей на каждой стадии дискретизации по времени, локализованной отдельно взятой вакуум-камерой обжиговой конвейерной машины, с использованием разработанной процедуры условной оптимизации, отличающейся ускоренным поиском условного экстремума критерия энергоресурсоэффективности, позволяет быстро находить научно обоснованные оптимальные по энергоресурсоэффективности режимы функционирования ХТС в зоне сушки конвейерных обжиговых машин [11].
Работа выполнена в рамках базовой части государственного задания Минобрнауки России на выполнение государственных работ в сфере научной деятельности, проект № 13.9597.2017/БЧ.
Библиографическая ссылка
Бобков В.И. ОПТИМИЗАЦИЯ ХИМИКО-ТЕХНОЛОГИЧЕСКОГО ПРОЦЕССА СУШКИ В СТАЦИОНАРНОМ РЕЖИМЕ МНОГОСЛОЙНОЙ МАССЫ ФОСФОРИТОВЫХ ОКАТЫШЕЙ ПО КРИТЕРИЮ ЭНЕРГОРЕСУРСОЭФФЕКТИВНОСТИ // Современные наукоемкие технологии. – 2018. – № 5. – С. 25-29;URL: https://top-technologies.ru/ru/article/view?id=36985 (дата обращения: 23.11.2024).