Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Шмырин А.М. 1 Мишачёв Н.М. 1 Канюгина А.С. 1

---

1 ФГБОУ ВО «Липецкий государственный технический университет»

В статье дается определение статических и динамических окрестностных систем на языке метаграфов. Управление сложным производственным процессом вблизи номинального режима обычно осуществляется в предположении, что такому режиму соответствует стационарная точка гипотетической глобальной динамической модели, и потому статические окрестностные системы в этом случае являются удобным средством локального моделирования. Достаточно типичной является ситуация, когда номинальных режимов несколько и переходы между ними осуществляются дискретно или непрерывно в зависимости от входных данных. Мы рассматриваем задачу объединения локальных статических окрестностных систем (моделей) в общую квазистатическую систему c коэффициентами, зависящими от входных данных. Предлагаются две версии такого объединения: дискретная и непрерывная. Обе они основаны на кластеризации входных данных окрестностной системы. В дискретной версии выбор текущей локальной модели определяется центром кластера. В непрерывной версии используются линейные комбинации локальных моделей с весами, образующими ассоциированное с кластеризацией разбиение единицы. В качестве примера применения решается задача объединения локальных окрестностных моделей стадии диффузии производства сахара, полученных в результате параметрической идентификации на основе выборки данных производства АО АПО «Аврора» «Боринский сахарный завод».

Статья в формате PDF

0 KB

окрестностные структуры

окрестностные системы

метаграфы

квазистатические системы

кластеризация

параметрическая идентификация

производство сахара

1. Шмырин А.М. Окрестностные системы и алгоритм Качмажа / А.М. Шмырин, Н.М. Мишачёв // Вестник Тамбовского университета. Сер. Естественные и технические науки. – 2016. – Т. 21, Вып. 6. – С. 2113–2120.

2. Шмырин A.M. Параметрическая идентификация линейной блочно-регрессионной окрестностной модели стадии диффузии производства сахара / А.М. Шмырин, Н.М. Мишачёв, А.С. Канюгина, А.А. Канюгин, В.О. Богатырёв // Modern informatization problems in the technological and telecommunication systems analysis and synthesis: Proceedings of the XXII-th International Open Science Conference (Yelm, WA, USA, January 2017). – Yelm, WA, USA: Science Book Publishing House. – 2017. – P. 360–365.

3. Basu A., Blanning R. Metagraphs and their applications. – Springer, 2007. – 174 p.

4. Takagi T., Sugeno M. Fuzzy identification of systems and its applications to modeling and control // IEEE transactions on systems, man, and cybernetics. – 1985. – vol. 15, no. 1. – Р. 116–132.

5. Zsоfia Lendek, Thierry Marie Guerra, Robert Babuska, Bart De Schutter. Stability Analysis and Nonlinear Observer Design Using Takagi-Sugeno Fuzzy Models. – Springer, 2010. – 196 p.

6. Бугаенко И.Ф. Общая технология отрасли. Научные основы технологии сахара / И.Ф. Бугаенко, В.И. Тужилкин. – СПб.: ГИОРД, 2007. – 512 с.

7. Сапронов А.Р. Технология сахара / А.Р. Сапронов, Л.А. Сапронова, С.В. Ермолаев – СПб.: Профессия, 2015. – 296 с.

Цели и задачи исследования

Окрестностные системы, или окрестностные модели – это статические или дискретные динамические системы уравнений на графе. Уравнения окрестностной системы могут соответствовать либо вершинам графа, либо его ребрам (см. [1]). В первом случае мы называем окрестностную систему вертексной, во втором – реляционной. Уравнения окрестностной системы структурно идентифицированы по наборам входящих в них переменных: этот уровень структурной идентификации задается графом. В задачах управления производственными процессами такие системы возникают на этапе перехода от структурной схемы производства (графа) к математической модели. Для моделирования вблизи номинальных режимов, как правило, достаточно рассматривать статические линейные или билинейные системы уравнений. При наличии нескольких номинальных режимов во многих случаях имеет смысл, вместо усложнения уравнений, перейти к квазистатической схеме. В данной статье мы обсуждаем общую теоретическую задачу объединения нескольких локальных статических окрестностных систем в квазистатическую систему и, далее, применяем предлагаемую схему объединения в задаче моделирования стадии диффузии производства сахара, рассматривавшейся в [2].

Окрестностные структуры и окрестностные системы

Окрестностные структуры (см. [1]) являются средством формализации связей между элементами моделируемой системы. На их основе удобно строить математические модели следующего уровня (системы уравнений). Окрестностной структурой мы называем ориентированный граф 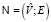, содержащий вершины 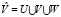трех типов: входы U, узлы V и выходы W, при этом:

- каждые два узла 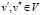, могут быть соединены между собой не более чем двумя противоположно ориентированными ребрами-связями e(v', v») и e(v», v');

- каждый узел 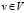имеет петлю e(v, v);

- каждый узел 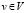имеет входящие и выходящие ребра (помимо петель);

- каждый вход 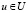имеет только выходящие ребра e(u, v);

- каждый выход 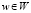имеет только входящие ребра e(v, w).

Как обычно, источниками вершины называются все входящие в нее вершины и стоками – все исходящие. Все узлы (то есть вершины 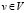) из-за наличия петель являются своими стоками и источниками, все входы имеют только стоки и все выходы – только источники.

Окрестностные системы удобно описывать с помощью понятия метаграфа (см., например, [3]). Нам потребуется только определение метаграфа: метавершинами MV метаграфа 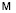называются подмножества некоторого конечного множества V, а метаребрами ME – пары метавершин. Или, на языке теории множеств: метавершины метаграфа – это элементы первого булеана 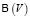, то есть 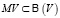, а метаребра метаграфа – это двухэлементные подмножества второго булеана 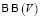, то есть 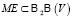. По аналогии с обычными графами можно определить ориентированные метаграфы и двудольные метаграфы. В окрестностной структуре 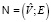каждый узел 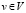порождает метавершину источников (метаисточник) 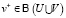и метавершину стоков (метасток) 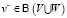, при этом 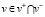. Обозначим через V+ и V– множества всех метаисточников и метастоков. Добавим еще к множеству метавершин все узлы 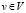. Каждый узел 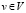порождает метаребро (v+, v), соединяющее метаисточник узла с этим узлом, и метаребро (v+, v–), соединяющее метаисточник узла и его метасток. Таким образом, каждая окрестностная структура 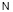порождает ориентированные двудольные метаграфы 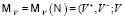и 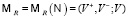. Метаграф 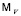мы будем называть вертексным, а метаграф 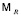– реляционным. Эти метаграфы соответствуют вертексным и реляционным окрестностным системам над окрестностной структурой 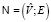, или системам для узлов и для ребер (см. [1]). Опишем подробнее эти системы. Обозначения множеств вершин U, V, W и метаузлов v+, v– можно понимать и как обозначения соответствующих наборов чисел – номеров вершин. Каждому ребру e(i, k), включая петли, соответствует переменная 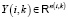входа-выхода из i-го узла в k-й. Переменные Y(i, k) = U(i, k) с i 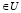мы называем входами, переменные Y(i, k) = W(i, k) с 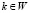– выходами, переменные Y(i, k) = V(i, k) с i, 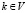– внутренними переменными. Для петель e(i, i) положим Y(i, i) = X(i) и 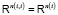. Переменную Y(i, i) = X(i) мы называем состоянием узла. В вертексной модели вход-выход Y(i, k) не зависит от k, то есть узел 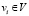передает по всем исходящим связям одну и ту же переменную своего состояния X(i) = Y(i, i), а вход 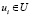– одну и ту же переменную входа 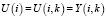. 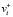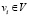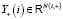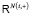Далее, метаисточникам узлов соответствуют переменные состояния метаисточника , где – это произведение всех пространств 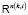c 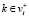. 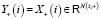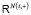В вертексном случае мы полагаем , где – это произведение всех пространств 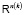c 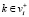. 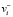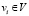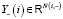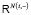Метастокам узлов соответствуют переменные состояния метастока , где – это произведение всех пространств 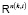c 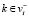. Вертексному метаграфу 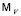соответствует набор (мета)функций

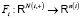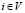, , (1)

каждая из которых преобразует состояние X+(i) метаисточника узла в состояние X(i) этого узла. Реляционному метаграфу 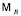соответствует набор (мета)операторов

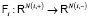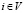, , (2)

каждый из которых преобразует состояние Y+(i) метаисточника узла i в состояние Y–(i) метастока этого узла. Уравнения статической вертексной системы имеют вид

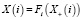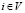, , (3)

здесь 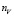уравнений, а уравнения статической реляционной системы имеют вид

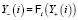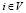, , (4)

здесь 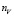операторных уравнений. Подробнее:

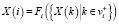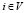, , (5)

,

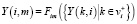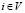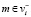, . (6)

В последнем случае количество уравнений равно 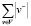, где 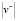– это количество вершин в метастоке v–. Динамические версии систем (3) и (4) имеют соответственно вид

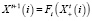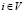, , (7)

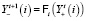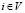, . (8)

Квазистатические окрестностные системы

При моделировании производственного процесса вблизи номинального режима во многих случаях можно считать, что такому режиму соответствует стационарная точка гипотетической глобальной динамической модели процесса, и потому в качестве локальной модели можно использовать статическую линейную или билинейную окрестностную систему. Далее, достаточно типичной является ситуация, когда номинальных режимов несколько и диспетчер производства изменяет управляющие переменные в зависимости от входных данных. Построения более сложной динамической модели, описывающей переходные режимы (а не только номинальные) на основе данных наблюдений, то есть регрессионными методами, обычно не дает хороших результатов. Поэтому при моделировании процессов с несколькими номинальными режимами имеет смысл, вместо усложнения уравнений, перейти к следующей квазистатической схеме. Множество вершин-входов U можно считать состоящим из независимых внешних входов 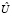и зависимых (управляемых) входов 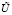. Соответственно, переменные U(i, k) бывают двух типов: внешние 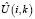и управляемые 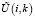. Обозначим через 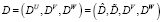множество всех кортежей состояний системы (то есть значений входов, внутренних переменных и выходов) во все моменты наблюдения. Пусть NU – размерность пространства всех входов. Тогда 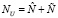, где 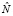– размерность пространства внешних входов, и 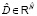. Можно предполагать, что множеству номинальных режимов соответствует кластеризация множества входных данных 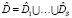с центрами кластеров 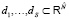. Для определенности мы рассматриваем далее только случай реляционных систем (для вертексных все аналогично). Обозначим через 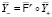регрессионные модели, то есть системы вида (4), построенные для каждого из номинальных режимов 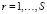в результате параметрической идентификации по соответствующим кортежам данных («номинальные» модели). Здесь – покомпонентное действие вектора метаоператоров 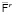на вектор метаисточников 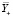(операторное произведение Адамара). Очевидным образом определены линейные комбинации 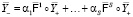этих моделей. Квазистатической окрестностной системой мы называем систему вида

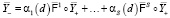(9)

c коэффициентами, зависящими 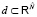, такими что 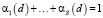, 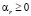. Для 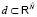обозначим через s(d) номер ближайшего к d центра кластера; если таких центров несколько, то s(d) – наименьший из номеров. Пусть 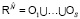– соответствующее разбиение пространства 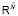(разбиение Дирихле – Вороного) и χr(d) – характеристические функции множеств 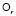. Дискретной композицией номинальных моделей 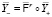мы называем квазистатическую систему

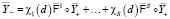. (10)

Для внешнего входа 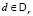эта система совпадает с номинальной 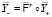. Далее, для каждого из множеств 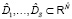вычислим ковариационную матрицу и обозначим через φ1,…,φS соответствующие 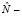мерные нормальные плотности с центрами 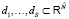. Положим

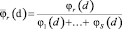. (11)

Функции 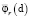образуют разбиение единицы на пространстве 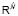. Непрерывной нормальной композицией номинальных моделей 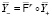мы называем квазистатическую систему

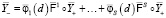. (12)

Замечание. Вместо многомерного нормального распределения можно, если это удобно по каким-либо соображениям, использовать любое другое унимодальное многомерное распределение. Описанную конструкцию можно, при желании, интерпретировать как нечеткую модель Такаги – Сугено [4, 5], но в данном случае язык нечетких моделей Такаги – Сугено, отягощенный логическими обозначениями, является излишним.

Квазистатическая реляционная модель стадии диффузии производства сахара

Сахарное производство (см. [6, 7]) является сложным многостадийным производственным процессом. В работе [2] была предложена реляционная окрестностная модель стадии диффузии производства сахара и были приведены результаты параметрической идентификации этой модели в предположении линейности и на основе месячной выборки данных производства АО АПО «Аврора» «Боринский сахарный завод» с временным интервалом 10 минут, объем выборки n = 3472. При локальной идентификации регрессионных коэффициентов по данным, относящимся как к разным дням, так и к разным интервалам времени в течение одного дня, наблюдались значимые отклонения этих коэффициентов от глобальных, вычисленных по всей выборке. Кроме того, в некоторых случаях наблюдались изменения наборов значимых предикторов. В то же время все полученные локальные линейные регрессионные зависимости соответствовали технологии сахароварения, а изменения коэффициентов достаточно хорошо объяснялись изменениями параметров свекловичной стружки. Поэтому, сохраняя структуру реляционной окрестностной модели, предложенной в [2], мы рассмотрели квазистатическую линейную модель, в которой коэффициенты зависят от входных параметров: дигестии (сахаристости) S и длины L свекловичной стружки (в [2] эти параметры обозначались соответственно, Y4 (0,1) и Y2 (0,1)). На рис. 1 приведены точки рассеяния двумерного вектора входных данных, где L – длина 100 г стружки (в метрах), S – дигестия сахарной стружки (в процентах). Гистограмммы каждой из координат имеют по две достаточно хорошо заметных моды, и потому при кластеризации по методу k-средних мы полагали k = 4. Средние кластеров указаны в таблице; на рис. 2 четыре кластера выделены разными цветами.

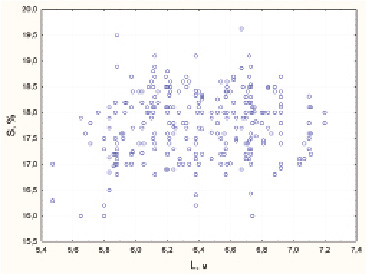
Рис. 1. Точки рассеяния двумерного вектора входных данных

Средние кластеров

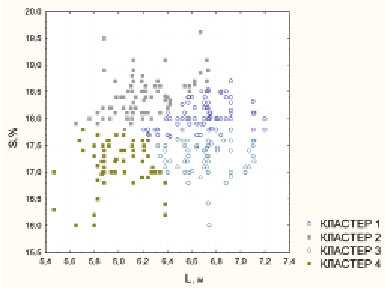
Рис. 2. Кластеры входных данных

В каждом из кластеров не обнаружены значимые корреляции между координатами, и потому можно считать, что соответствующие ковариационные матрицы диагональны. Аппроксимирующие нормальные плотности для кластеров имеют вид

Для кластера 1:

;

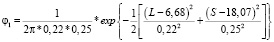Для кластера 2:

;

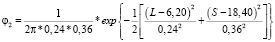Для кластера 3:

;

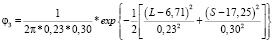Для кластера 4:

.

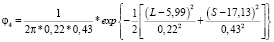Результаты параметрической идентификации коэффициентов уравнений для каждого из кластеров, по сравнению с опубликованными ранее в [2] результатами идентификации по всей выборке, оказались более устойчивыми относительно временных сдвигов.

Выводы

Квазистатические окрестностные системы являются удобным средством моделирования объектов с несколькими номинальными режимами, зависящими от входных данных. В случае, когда каждый из номинальных режимов достаточно хорошо описывается линейной моделью, их квазистатическая композиция (дискретная или непрерывная) сохраняет преимущества линейности, критически важные в задаче управления.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 16-07-00854).

Библиографическая ссылка