При проектировании теплозащитной одежды определяющая роль в обеспечении необходимой величины теплоизоляции отведена утепляющим материалам. Современный ассортимент несвязных утеплителей отличается большим разнообразием материалов как натурального (перо-пуховая смесь), так и синтетического (hollowfiber, fibertech и др.) происхождения [1, 2]. Появление новых объемных несвязных материалов для одежды, разнообразных по строению, требует оценки и прогнозирования изменения теплофизических свойств в процессе эксплуатации [3].
Отдельные участки одежды подвергаются многократной деформации сжатия в результате воздействия ветра и движения человека. Утеплитель сжимается даже под действием сравнительно небольших по величине сил, что приводит к уменьшению его толщины, уплотнению и влечет за собой ухудшение расчетных значений теплозащитных характеристик одежды. В настоящее время остаются нерешенными вопросы, связанные с учетом и прогнозированием этих изменений, а также автоматизацией процесса проектирования теплозащитной одежды для сокращения временных и материальных затрат при обеспечении ее качества [4].
Современные компьютерные технологии позволяют прогнозировать изменение свойств материалов с учетом деформационных характеристик, используя математические модели. Компьютерное моделирование отличается универсальностью, не требует специального оборудования и является достаточно объективным [5]. Таким образом, разработка математической модели является актуальным направлением автоматизации проектирования теплозащитной одежды.
Цель исследования
Разработать математическую модель для описания процесса сжатия несвязных утеплителей, устанавливающую зависимость между временем нагружения, давлением и изменением плотности, определяющую деформационные характеристики образца материала, с применением компьютерных технологий.
Материалы и методы исследования
Для достижения поставленной цели необходимо провести испытания утепляющих материалов и провести оценку результатов кинетики сжатия. В качестве объектов исследований выбраны объемные несвязные утеплители – гусиный пух категории «Экстра» (96 % пух, 4 % мелкое перо) и hollowfiber из синтетических волокон. Исследуемые теплоизоляционные материалы рассматриваются как вязкоупругое тело, которое в результате многократного сжатия изменяет свои физико-механические свойства [6]. Изменение объемной плотности утеплителя зависит от его реологических свойств, давления и времени воздействия на утеплитель.
Для проведения испытаний была разработана и изготовлена экспериментальная установка, реализующая метод одноосного сжатия. Получение информации о величине и скорости сжатия утеплителя основано на использовании датчика линейного перемещения. Данные передаются на персональный компьютер и обрабатываются программой [7], которая позволяет рассчитывать реологические характеристики исследуемого материала. В методике проведения исследований были учтены потери на трение исследуемого материала о боковые стороны цилиндра установки. При сжатии утеплителя выполняли расчет его текущей высоты в установке hi по формуле (1), высотной деформации εh по формуле (2) и текущее значение плотности ρi, учитывая насыпную высоту h0, изменение высоты образца Δh за время t:
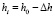, (1)
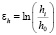. (2)
При этом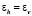 
, где εv – объемная деформация. Диапазон выбранных для исследования давлений от 0,041 до 2,0 кПа, что соответствует давлению человека на материалы при эксплуатации, а также воздействию ветровой нагрузки. Методика проведения исследования представлена на рис. 1.
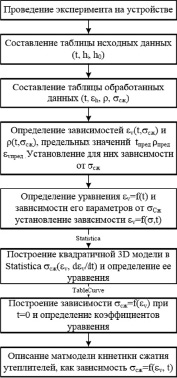
Рис. 1. Схема проведения исследования
Результаты исследования и их обсуждение
Согласно результатам исследований полученные зависимости εv(t, σсж) и ρ(t, σсж) влияния давления σсж и времени сжатия t на величину объемной деформации εv и плотности ρ показали, что существуют предельные значения времени tпред, плотности ρпред и объемной деформации εv пред. При этом при повышении нагрузки уменьшается предельное значение времени и объемной деформации, а также повышается предельное значение плотности.
Предельные нелинейные зависимости εvпред(σсж), ρпред(σсж), tпред(σсж) могут быть описаны сигмоидальным уравнением
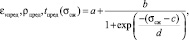(3)
где a, b, c, d – коэффициенты уравнений.
Нелинейные зависимости εv(t) при σсж = const могут быть описаны логистическим уравнением
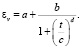(4)
При этом параметры логистического уравнения a, b, c, d зависят от сжимающего напряжения σсж. Используя программу TableCurve, установили связь от 0..tпред влияния времени сжатия на изменение величин, обеспечивающих переход от динамики к статике объемной деформации при фиксированной σсж, используя логистическую зависимость, учитывающую предельные значения:
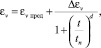(5)
где t = 0..tпред – время действия нагрузки, с,
εv = 0..εv пред – объемная деформация при t = 0..tпред,
tпред – предельное значение времени сжатия, характеризующее переход от динамического состояния к статическому, с,
εv пред – предельное значение объемной деформации, достигнутое при tпред,
Δεv – разность значений мгновенной и предельной деформации,
tn – время перехода кривой εv от выпуклой к вогнутой его части, с,
d – определяет степень кривизны, εv.
При этом параметры логистического уравнения зависят от сжимающего напряжения σсж и описываются сигмоидальной функцией:
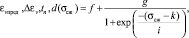(6)
где f, g, k, i – коэффициенты уравнений.
Логистическую зависимость (5) записали в виде, учитывающем влияние σсж на коэффициенты уравнения:
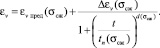(7)
Для определения скорости деформации ?v продифференцировали объемную деформацию (4) по времени t с использованием программы Mathcad 15:
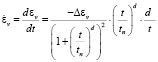. (8)
Используя полученное уравнение (8), построили зависимости ?v (t) при фиксированных σсж в среде «Statistica» (рис. 2).
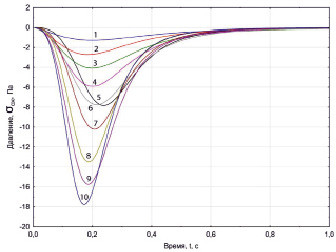
Рис. 2. Зависимость ?v от t при фиксированных значениях σсж, Па. 1 – 41, 2 – 83, 3 – 124, 4 – 165, 5 – 248, 6 – 330, 7 – 413, 8 – 826, 9 – 1652, 10 – 2064
Зависимости ?v(t) (рис. 2) носят экстремальный характер. Минимальные значения ?v(t) наблюдаются при критическом времени tкр = 0,17–0,22. Повышение давления приводит к увеличению абсолютного значения скорости деформации. С увеличением времени t > tкр значения функции |?v(t)| уменьшаются и стремятся к 0. Построили с помощью программы «Statistica» квадратичную 3D модель σсж(?v, εv) при условиях t < tпред и εv < εv пред для натурального и синтетического утеплителя (рис. 3) и определили ее параметры:
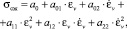(9)
где а0, а01, а02, а11, а12, а22 – параметры уравнения сжатия.
Влияние εv на σсж носит экстремальный характер. Максимальные значения σсж наблюдаются для перо-пуховой смеси «Экстра» при εv пред = –1,4 (рис. 3, а). Максимальные значения σсж для hollowfiber наблюдаются при εv пред = –0,7 для σсж = –200 и при εv пред = –0,2 для σсж = –1300 (рис. 3, б). Параметры уравнения уплотнения при εv > εv пред, εv < εv пред и для всего исследуемого диапазона значений представлены в таблице.
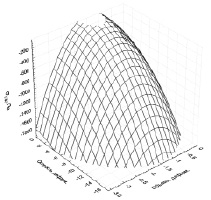
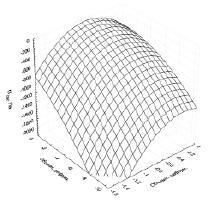
а б
Рис. 3. 3D модель σсж(?v, εv): а – перо-пуховая смесь, б – hollowfiber
Параметры уравнения сжатия
|
Вид утеплителя |
Исследуемый диапазон |
а0 |
а01 |
а02 |
а11 |
а12 |
а22 |
|
Перо-пуховая «Экстра» |
εv = 0..–3,6 |
–739,99 |
–1085,35 |
–3,51 |
–385,59 |
–2,62 |
–7,37 |
|
Hollowfiber |
εv = 0..–1,6 |
–471,18 |
–1231,70 |
–6,31 |
–905,55 |
–73,54 |
–8,69 |
Из представленных графиков видно, что характер зависимости синтетического утеплителя значительно отличается от характера зависимости натурального, которые имеют симметричный вид относительно предельной объемной деформации. Характер зависимости σсж(?v, εv) для hollowfiber значительно меняется с увеличением объемной деформации выше критической. Данное явление характерно для исследуемого диапазона значений давления сжатия.
Зависимость влияния времени нагружения и деформации материала утеплителя на напряжение σ могут быть описаны уравнениями изохронных кривых. Для описания зависимости σсж(εv, t) для несвязного объемного утеплителя уравнение изохронных кривых представили в виде
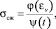(10)
где φ(εv) – кривая мгновенного деформирования,
ψ(t) – зависимость, учитывающая время.
Подставляя данные, рассчитанные по формуле (4) при t = 0 в TableCurve, построили кривую мгновенного деформирования (уплотнения) φ(εv), используя импульсную зависимость, и определили коэффициенты уравнения:
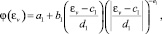(11)
где а1, b1, c1, d1, e1 – коэффициенты уравнения,
зависимость, учитывающую время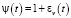 
, с учетом (10), записали в виде
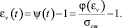(12)
Отсюда в TableCurve построили кривую мгновенного деформирования и определили зависимость εv(t) и коэффициенты:
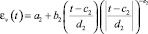, (13)
где a2, b2, c2, d2, e2 – коэффициенты уравнения.
С учетом (11) и (13) уравнение (10) принимает вид
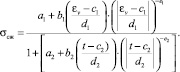(14)
Данное уравнение позволяет адекватно описать результаты экспериментальных исследований кинетики сжатия несвязного объемного утеплителя.
Заключительный этап анализа полученной математической модели предусматривает проверку ее адекватности. Уравнение (14) можно считать адекватным с 95 % доверительной вероятностью, учитывая, что Fp < Fтабл. Данная модель позволяет достоверно описать результаты экспериментальных исследований кинетики сжатия несвязного объемного утеплителя. Модель легко адаптируется под различные объемные несвязные утеплители за счет применения коэффициентов уравнения и доступности программного обеспечения.
Выводы
Разработана методика и экспериментальная установка для исследования процессов сжатия утеплителя, которая позволяет определить время и скорость деформации при фиксированных значениях нагрузки.
В результате проведенного комплекса исследований установлен характер влияния давления и времени сжатия на величину объемной деформации. Выявлен экстремальный характер зависимости скорости деформации от времени.
Построена квадратичная реологическая 3D модель, описывающая влияние объемной деформации и скорости объемной деформации на давление сжатия.
Разработана математическая модель, которая позволяет определить деформационные характеристики утеплителя и прогнозировать теплозащитные свойства материалов в процессе эксплуатации одежды под действием различных нагрузок.
Библиографическая ссылка
Рукавишникова А.С. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ПРОЦЕССА СЖАТИЯ ОБЪЕМНЫХ УТЕПЛИТЕЛЕЙ ДЛЯ ПРОЕКТИРОВАНИЯ ТЕПЛОЗАЩИТНОЙ ОДЕЖДЫ // Современные наукоемкие технологии. – 2018. – № 4. – С. 113-117;URL: https://top-technologies.ru/ru/article/view?id=36969 (дата обращения: 21.11.2024).