Шифр MITSY1 был представлен на конкурс проектов NESSIE и стал одним из трех победителей в категории симметричных блочных шифров [1]. Подробное описание шифра можно найти в обзоре С. Панасенко [2]. Шифр MITSY1 интересен еще и тем, что позже он был представлен на конкурс CRYPTREC по выбору криптостандарта Японии и вошел в состав шифров-победителей [3]. В настоящей работе рассматривается возможность применения метода дифференциального анализа к упрощенной версии шифра MISTY1. При проведении исследований стойкости современных шифров часто применяется практика рассмотрения упрощенных версий шифров. Это делается для детального и более подробного изучения отдельных компонентов шифра с тем, чтобы в дальнейшем иметь возможность перейти к рассмотрению полной версии шифра.
Алгоритм MISTY1 основан на «вложенных» сетях Фейстеля. Сначала 64-битный шифруемый блок данных разбивается на два 32-битных подблока, после чего выполняется r раундов следующих преобразований (рис. 1). В нечетных раундах каждый подблок обрабатывается функцией FO. Правый подблок складывается по модулю два с левым подблоком, прошедшим через функцию FO. Подблоки меняются местами. После заключительного раунда оба подблока обрабатываются операцией FL.
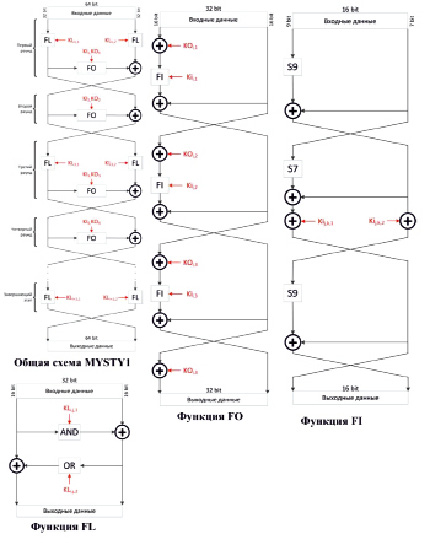
Рис. 1. Структура шифра MYSTY1
Операция FL работает следующим образом (рис. 1). Обрабатываемый 32-битный блок разбивается на два 16-битных подблока. Сначала правая часть блока складывается по модулю два с результатом операции «логическое И» для левой части блока и одним из подключей. После этого левая часть исходного блока складывается по модулю два с результатом операции «Логическое ИЛИ» для преобразованной правой части и второго подключа.
Операция FO представляет собой функцию вложения второго уровня (рис. 1). Здесь выполняется разбиение входного блока на два равных фрагмента по 16 бит, которые проходят 3 раунда следующих преобразований. Левая половина блока складывается по модулю два (операцией XOR) с раундовым подключом KOi,k, где k – номер раунда функции FO. После этого левая часть блока преобразуется с помощью операции FI. Левая половина блока складывается по модулю два (XOR) с правой половиной блока. После этого левая и правая половины меняются местами. После последнего раунда левая часть блока складывается по модулю два (XOR) c последним подключом KOi,k.
Операция FI представляет собой третий уровень вложенности сети Фейстеля (рис. 1). В данном случае сеть Фейстеля является несбалансированной, так как левая и правая части сети имеют разное количество обрабатываемых битов. Обрабатываемый блок делится на два подблока длиной 9 и 7 бит (левая и правая части). Затем выполняются 3 раунда следующих преобразований. Левая часть проходит через S-блок замены. При этом в 1 и 3 раундах левая часть содержит 9 битов и обрабатывается таблицей S9, во втором раунде левая часть содержит 7 битов и обрабатывается таблицей S7. После этого левая часть блока складывается с правой частью по модулю два (операция XOR). При этом, если справа расположена 7-битная часть, то она дополняется нулями слева до 9 бит. Если же справа расположена 9-битная часть, то у нее не учитываются два старших бита (слева). Во втором раунде левая часть блока складывается по модулю два (операция XOR) с раундовым подключом KIi,k,1, а правая часть блока – с подключом KIi,k,2. В остальных раундах эти действия не выполняются. После этого левая и правая части меняются местами.
Расшифрование производится выполнением тех же операций, но со следующими изменениями. Фрагменты расширенного ключа используются в обратной последовательности. Вместо функции FL используется обратная ей функция FL-1.
Подключи вырабатываются согласно схеме, изображенной на рис. 2. Ключ длиной 128 бит делится на 8 подключей по 16 бит и каждая из них подается на вход блока FI, а в качестве ключа подается следующий подключ. Для последнего подключа, подаваемого как текст, в качестве ключа подается первый подключ. Красными линиями обозначена подача ключа в блок FI. Получившиеся подключи обозначаются штрихом. Необходимые фрагменты расширенного ключа «набираются» согласно таблице и используются во всех функциях шифра MYSTY1 (рис. 1).
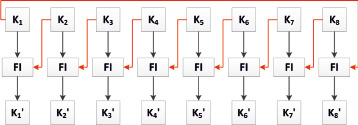
Рис. 2. Схема выработки подключей
Выборка подключей
|
Назначение |
KOi,1 |
KOi,2 |
KOi,3 |
KOi,4 |
KIi,1 |
KIi,2 |
KIi,3 |
|
Фрагмент |
Ki |
Ki+2 |
Ki+7 |
Ki+4 |
K′i+5 |
K′i+1 |
K′i+3 |
|
Назначение |
KLi,1,1 |
KLi,2,1 |
KLi,1,2 |
KLi,2,2 |
|||
|
Фрагмент |
K(i+1)/2 |
K′(i+1)2+2 |
K′(i+1)2+6 |
K(i+1)2+4 |
|||
Метод дифференциального криптоанализа впервые был предложен в начале 1990-х гг. Э. Бихамом и А. Шамиром для анализа алгоритма шифрования DES. Хотя в книге Б. Шнайера упоминается о том, что разработчики алгоритма DES знали о возможности такого анализа еще во время разработки алгоритма в 1970-х гг., широкая общественность узнала о дифференциальном криптоанализе именно из работ [4, 5]. С помощью метода дифференциального криптоанализа сложность анализа алгоритма DES сократилась до 237. Дальнейшее развитие этого метода показало возможность его применения к целому классу различных видов шифров, позволило выявить слабые места многих используемых и разрабатываемых алгоритмов шифрования. Сегодня этот метод, а также некоторые его производные, такие как метод линейно-дифференциальный, метод невозможных дифференциалов, метод бумеранга, широко используются для оценки стойкости вновь создаваемых шифров [6].
Анализ S-блоков. Число раундов MISTY1 должно быть всегда кратным 4, рекомендуемым же является MISTY1 с 8 раундами. В целях наилучшего понимания механизмов шифра и его подверженности дифференциальным атакам на старте были приняты следующие решения. Рассматривать упрощенную модель MISTY1. Для этого убрать из алгоритма шифра все FL-функции. Сократить рекомендуемые 8 раундов до четырех (тем самым мы не будем нарушать целостности шифра, которая также обеспечивается кратностью, но проанализируем более короткую версию шифра).
Начальными элементами, от которых следует отталкиваться при дифференциальном анализе, являются нелинейные блоки. В шифре MYSTY1 есть два блока замены: S7 и S9. Первый этап дифференциального анализа заключался в построении таблиц вероятностей для этих блоков замен. Таблица вероятности представляет собой по горизонтали входящую разность текстов, по вертикали – выходящую разность текстов, а на пересечении вероятность соответствия выходной разности заданной входной разности. Алгоритм анализа дифференциальных свойств нелинейных блоков приведен в работе [7]. В результате анализа было показано, что любая входная разность текстов приводит к любой выходной разности либо с вероятностью 0, либо с вероятностью 2 к 128 или 512 соответственно для блоков S7 и S9. Также важно отметить, что входная разность, равная нулю, с вероятностью 100 % даст на выходе S-блока также нулевую разность.
Анализ функции FI. При анализе функции FI было сделано предположение, что есть такая разность ΔA, которая может отразиться сама в себя. То есть S9(ΔA) = S7(ΔA) = ΔA. Для подтверждения этого факта был разработан алгоритм и проанализированы таблицы с вероятностями для входных-выходных разностей блоков S7 и S9. После анализа S-блоков было обнаружено 33 варианта ΔA, которая отражалась бы сама в себя. На рис. 3 показаны три варианта прохождения входной разности через функцию FI, в случае, когда значение разности после S-преобразования остается неизменным. В первом варианте (рис. 3, а) левая половина разности равна значению ΔA1, правая часть разности равна нулю (Δ0). Во втором варианте (рис. 3, б) левая половина разности равна нулю (Δ0), а правая часть разности равна значению ΔA1. В третьем варианте (рис. 3, в) обе части разности равны значению ΔA1. Для дальнейшего анализа мы будем использовать второй вариант схемы, приведенный на рис. 3, б.
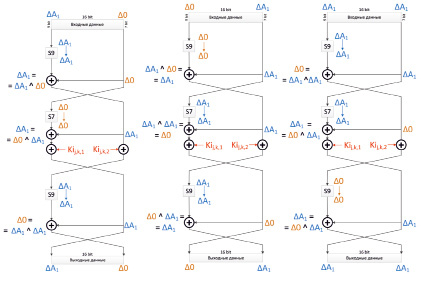
а) б) в)
Рис. 3. Различные схемы преобразования разностей с помощью функции FI
Анализ функции FO. Для построения разностных схем функции FO можно использовать тот же принцип, что и для функции FI. Будем рассматривать случаи, когда преобразование FI оставляет входную разность неизменной. Нами было рассмотрено несколько вариантов построения подобных схем, три из которых представлены на рис. 4. При выборе схемы для дальнейшего анализа мы руководствовались тем, какую ключевую информацию нам позволит извлечь рассматриваемая схема. Так, схема, приведенная на рис. 4, в, позволит нам определить только ключ KOi,2. Вариант, представленный на рис. 4, а, даст нам возможность найти ключи KOi,1 и KOi,3, но строго последовательно, т.е. мы сможем найти KOi,3 и KIi,3 только после того, как найдем KOi,1 и KIi,1. Вариант, представленный на рис. 4, б позволяет найти ключи KIi,2, KOi,2 и KIi,1, KOi,1 независимо друго от друга. Поэтому дальнейший анализ основывается на схеме, представленной, на рис. 4, а.
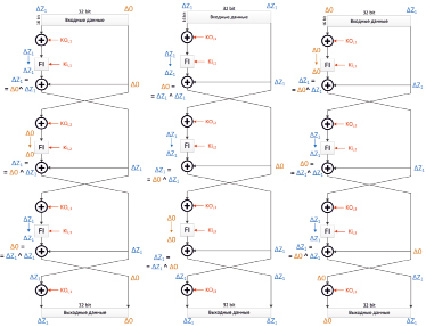
а) б) в)
Рис. 4. Различные схемы преобразования разностей с помощью функции FO
Анализ основной функции MISTY1. Для построения схем отображения разностей при выполнении основного преобразования шифра MISTY1, был использован эффект отражения разности в самой себя. При построении разностей учитывались те варианты, которые позволяют получить максимальную вероятность дифференциала (то есть определение выходной разности, вероятность получения которой является максимально возможной). Наиболее подходящие схемы из всех рассмотренных схем при выполнении анализа представлены на рис. 5.
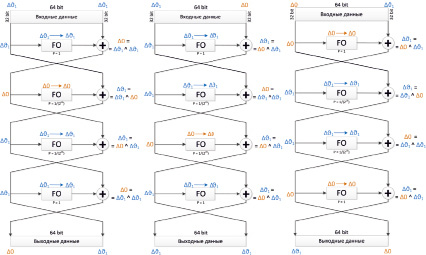
а) б) в)
Рис. 5. Различные схемы преобразования разностей для 4 раундов шифра MISTY1
Исходя из вариантов, представленных на рис. 5, можно определить, какую часть секретного ключа можно будет определить с использованием данных разностных схем. Так, с помощью схемы, представленной на рис. 5, а, можно проанализировать блоки FO1 и FO4 параллельно. Блок FO2 не может быть подвергнут анализу из-за нулевой разности, а блок FO3 из-за того, что он зависит от блока FO2. С помощью схемы, представленной на рис. 4, б, можно независимо проанализировать блоки FO1, FO4. После этого можно будет извлечь информацию из блока FO2. Блок FO3 придется пропустить из-за нулевой разности. Схема, представленная на рис. 5 в, является самой малоинформативной, так как имеет в своем составе сразу два блока с нулевой разностью. Выбирая между схемами, представленными на рис. 4, а и б, стоит учесть, что для схемы 4, а, подбор подключей будет проводиться по первому и последнему раунду, а для схемы 4, б, – по первому и второму (последовательно). При этом вероятность нахождения правильных пар текстов для обеих схем составит 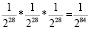 .
.
В связи с тем, что для поиска правильных пар текстов, удовлетворяющих заданным вероятностям, необходимо проанализировать большое количество пар текстов, в данном случае целесообразно использовать технологии распределенных многопроцессорных вычислений, такие как MPI и NVIDIA CUDA [8, 9]. Согласно Парадоксу Дней Рождений [10], проанализировав 242 пар текстов, можно найти правильную пару текстов с вероятностью р = 0,5. Экспериментальные данные при поиске дифференциалов для шифра MYSTI1 на основе технологии MPI были получены с использованием семи двухъядерных вычислительных узлов Intel Core i5 – 3320М CPU, 2.60 GHz, 4 Gb RAM. Среднее время обработки 242 пар текстов с использованием 14 процессоров составило в среднем 900 часов (15 дней). При использовании технологии NVIDIA CUDA вычисления производились на ПК Intel i5 2400 NVIDIA GTS 459 8 Gb RAM. Было показано, что при количестве процессоров, равном 1024, среднее время вычислений составляет 640 минут (около 11 часов).
В заключительном этапе анализа был реализован алгоритм поиска битов секретного ключа. Так, для схемы 5, б, был предложен алгоритм, состоящий из трех этапов. На первом этапе, анализируя значения разностей, аналитик может восстановить раундовые подключи К1, К3, К4, К8 и К'1, K'4, K'6, K'7. На втором этапе, используя уже найденные значения подключей, аналитик может восстановить связанные с ними раундовые подключи: К2, К5, К7 и К'3, K'8. К сожалению, в данном случае нельзя получить информацию о раундовых подключах К6 и К'2, K'5 – их можно определить только перебором.
Работа выполнена при поддержке гранта РФФИ № 17-07-00654-а.
Библиографическая ссылка
Ищукова Е.А., Куликов А.В. НЕКОТОРЫЕ ПОДХОДЫ К ДИФФЕРЕНЦИАЛЬНОМУ АНАЛИЗУ УПРОЩЕННОГО ШИФРА MISTY1 // Современные наукоемкие технологии. 2018. № 4. С. 55-61;URL: https://top-technologies.ru/ru/article/view?id=36959 (дата обращения: 13.02.2026).



