Выбор аптечной организации в качестве объекта исследования для формирования системы управления запасами интересен с той точки зрения, что для неё в гораздо большей степени актуальны научные основы эффективного управления запасами. Даже небольшие аптеки с малым торговым залом насчитывают не менее 2–3 тыс. номенклатурных позиций. Поэтому правильное планирование и управление запасами лекарственных средств становится жизненно необходимым для успешного функционирования аптечных организаций [1, 2].
Важнейшим фактором в задаче управления запасами является спрос на запасы. В тех случаях, когда спрос на запасы достоверно известен, применяются детерминированные модели управления запасами. Широкое распространение для определения запасов в условиях детерминированного спроса на запасы получила формула Уилсона [3–5]. В то же время формула Уилсона пригодна лишь для тех случаев, когда спрос на запасы заранее установлен, объёмы запасов уменьшаются с заданной интенсивностью, как только они достигают нуля, следует заказ новой партии запасов, которая поступает немедленно. Очевидно, что такого в практике аптек не встречается. Аптеки сталкиваются с проблемами задержки товара, фактический спрос на лекарства часто не совпадает с прогнозируемым, к моменту прибытия поставки данные, положенные в основу заказа, оказываются устаревшими, возникает дефицит отдельных лекарственных препаратов, зачастую имеет место затоваривание и списание лекарств в связи с истечением срока годности. Перечисленные факторы, действуя порознь или группируясь в различных сочетаниях, приводят к существенным издержкам аптечных организаций. Поэтому очевидно, что для повышения эффективности управления запасами необходимо применять научные методы управления запасами, учитывать вероятностный характер работы аптек и, в частности, случайную природу спроса на лекарственные средства.
Здесь и далее исследуется задача управления запасами с фиксированным размером заказа, которая означает, что размер поступающих партий запаса постоянен, заказ на поставку партии делается при уменьшении размера запаса до заранее установленного критического уровня, называемого «точкой заказа».
Цель исследования
Повышение эффективности аптечных организаций за счет совершенствования моделей и методов управления запасами лекарственных средств, которые учитывают вероятностный характер спроса на лекарственные средства.
Материалы и методы исследования
Стратегия с фиксированным размером заказа показала свою эффективность для ответственных запасов, поскольку предусматривает постоянный контроль за объёмом и наличием запасов, что обеспечивает более быструю реакцию на угрозу дефицита запаса. Искомыми переменными при данной стратегии являются «точка заказа» и объём заказываемой партии [3–5].
Исследование задачи управления запасами с позиций системного анализа показало, что стратегию управления запасами с фиксированным размером заказа можно рассматривать как задачу массового обслуживания [6–9]. Известно, что теория массового обслуживания, которую ещё называют теорией очередей, изучает структуру систем массового обслуживания (СМО) на основе исследования потоков заявок или требований, поступающих в систему на обслуживание в случайные моменты времени, а удовлетворение заявок или требований, называемое обслуживанием, осуществляется одним или несколькими обслуживающими устройствами. Если допустить, что требованиями или заявками в исследуемой СМО являются запасённые товары, а устройствами обслуживания – покупатели товаров, то зная интенсивность прибытия покупателей, которая характеризует спрос на товары, можно определить оптимальную интенсивность пополнения запасов товаров. Поэтому в данной работе задачу управления запасами с фиксированным размером заказа в аптечной организации проанализируем с помощью теории массового обслуживания.
Для установления закона распределения вероятностей спроса на лекарственные препараты была проведена статистическая обработка выборки данных на примере сбыта ряда лекарственных средств в МУП Ангарского городского округа «Аптека № 28».
На рис. 1 показаны временные ряды сбыта отдельных лекарственных средств за 2014–2015 гг.
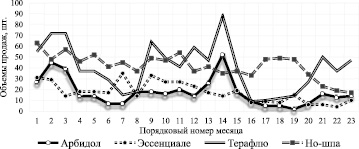
Рис. 1. Временные ряды сбыта отдельных лекарственных средств
На рис. 1 видно, что временные ряды содержат тренды, сезонную составляющую и случайные факторы, и показывают, что спрос на лекарственные средства в целом существенно нестационарен.
Исследование показало, что описать точно спрос на лекарства определённым законом распределения вероятностей для всей совокупности данных не представляется возможным. Однако, если разбить всю выборку данных на поддиапазоны, равные, например, горизонту управления запасами, можно достаточно точно аппроксимировать данные сбыта лекарственных средств на горизонте управления законом Пуассона [10].
Модель стратегии управления запасами с фиксированным размером заказа
Пусть прибытие покупателей в аптеку происходит с интенсивностью μ и имеет пуассоновское распределение. Это означает, что покупатели прибывают в аптеку в случайные моменты времени, причём вероятность прибытия одного покупателя в интервале времени от t до t + Δt равна μΔt и не зависит от t, а вероятность появления в этом интервале двух и более покупателей пренебрежимо мала. Такое допущение является достаточно обоснованным, если принять сколь угодно малым Δt.
Прибытие партии лекарственного средства (ЛС) в аптеку происходит с интенсивностью λ и также имеет пуассоновское распределение. Продолжительность времени с момента подачи заявки на пополнение запасов до момента прибытия запасов ЛС в аптеку имеет показательное распределение. В случае показательного закона в пуассоновском потоке событий время прибытия заказа составляет T = 1/λ.
Будем считать, что λ и μ определены и не зависят от времени на горизонте управления.
Пусть всегда, когда объем запасов ЛС в аптеке падает до критического уровня P, который будем называть «точкой заказа», заказывается Q единиц лекарственных средств, таким образом, что
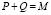 , (1)
, (1)
где M – максимальный объём лекарственного средства, который может принять аптека. Будем считать величину M заданной. Тогда определению подлежит либо точка заказа P, либо объём заказа партии Q для каждого лекарственного средства. Видно, что, определив одно из этих значений, второе находим из уравнения (1).
Обозначим как Sn состояние системы массового обслуживания (СМО), полагая, что СМО находится в состоянии Sn, когда в аптеке присутствует n единиц ЛС. Система покидает состояние Sn и переходит в состояние Sn+1, когда поступает дополнительная единица лекарственного средства, или в состояние Sn–1, когда единица ЛС продана покупателю. Применение стратегии «заказывать Q единиц ЛС, когда уровень запасов уменьшится до P, и заказывать M единиц ЛС, когда уровень запасов уменьшается до нуля», будет означать, что:
1) система массового обслуживания переходит из состояния Sn в состояние Sn–1 при продаже одной единицы лекарственного средства с интенсивностью μ;
2) система переходит из состояния Sn (n ≠ 0) в состояние Sn+Q, а из состояния S0 в состояние SM, при восполнении запаса с интенсивностью λ.
Схема случайного процесса, например, для системы S с шестью состояниями (M равно пяти, а P двум единицам лекарственных средств) показана на рис. 2.
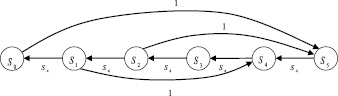
Рис. 2. Схема случайного процесса движения запасов
На рис. 2 видно, что при отсутствии запасов ЛС формируется заказ на пополнение запаса до величины M, т.е. пяти единиц. Как только запас ЛС сокращается до двух единиц, следует заказ ЛС в количестве трёх единиц. Момент поступления заказанной партии ЛС может наступить: до прибытия очередного клиента, и тогда система перейдёт из состояния S2 в состояние S5; либо после прибытия очередного клиента и продажи ему единицы ЛС, и тогда система перейдёт из состояния S1 в состояние S4 и т.д.
Обозначим через Pn вероятность того, что в наличии имеются n единиц ЛС, а через 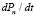 – скорость изменения состояния Sn. Тогда скорость изменения размеров запаса товара можно определить с помощью уравнений Колмогорова [11].
– скорость изменения состояния Sn. Тогда скорость изменения размеров запаса товара можно определить с помощью уравнений Колмогорова [11].
Так, для системы на рис. 2 уравнения для вероятностей состояний примут вид
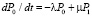 , (2)
, (2)
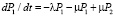 , (3)
, (3)
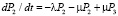 , (4)
, (4)
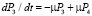 , (5)
, (5)
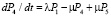 , (6)
, (6)
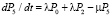 . (7)
. (7)
При постоянных интенсивностях λ и μ существует установившийся режим. В установившемся режиме система будет менять свои состояния, переходя из одного в другое, но вероятности этих состояний уже не будут зависеть от времени. Значения вероятностей для системы, находящейся в установившемся режиме, могут быть получены из системы (2)–(7), в которой 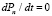 для всех n.
для всех n.
Решения системы уравнений (2)–(7) для установившегося режима принимают вид
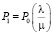 , (8)
, (8)
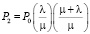 , (9)
, (9)
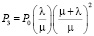 , (10)
, (10)
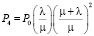 , (11)
, (11)
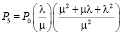 , (12)
, (12)
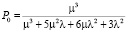 . (13)
. (13)
В общем виде уравнения для вероятностей состояний системы примут вид
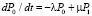 , (14)
, (14)
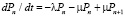 , для
, для 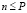 , (15)
, (15)
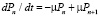 , для
, для 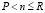 , (16)
, (16)
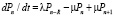 , для
, для 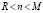 , (17)
, (17)
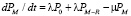 . (18)
. (18)
Решения системы уравнений (14)–(18) для установившегося режима:
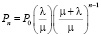 , для
, для 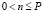 , (19)
, (19)
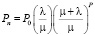 , для
, для 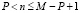 , (20)
, (20)
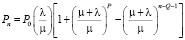 , для
, для 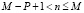 , (21)
, (21)
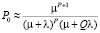 . (22)
. (22)
Среднее количество запасённых товаров в установившемся режиме определяется по формуле
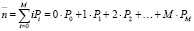 (23)
(23)
или
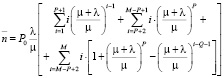 . (24)
. (24)
Выражение в скобках (24) представляет сумму из трёх рядов. Не приводя все математические выкладки, запишем окончательное выражение для определения среднего количества запасённых товаров, которое принимает вид
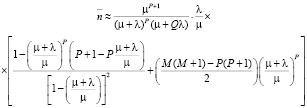 . (25)
. (25)
Формулы (22) и (25) являются приближёнными (аналитические выражения слишком громоздки). Однако отклонения результатов расчётов вероятности 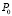 и
и 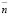 по точным и приближённым выражениям не отличались более чем на 11 % для различных M, P и Q.
по точным и приближённым выражениям не отличались более чем на 11 % для различных M, P и Q.
Пусть ϑ – розничная цена ЛС, ν – закупочная цена ЛС, C1 – затраты на оформление и выполнение заказа (не зависят от размера партии), C2 – затраты на хранение единицы ЛС. Если спрос на ЛС на горизонте управления равен μ, то количество заказов на горизонте управления будет равно μ/Q.
Тогда прибыль аптеки на горизонте управления
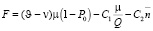
или с учётом выражений (22) и (25)
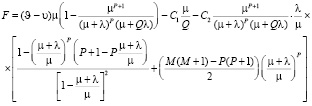 . (26)
. (26)
Искомыми переменными являются критический уровень запаса P и объём партии Q, максимизирующие F. Но поскольку P и Q связаны выражением (1), подставим в (26) M – P вместо Q. В результате получим
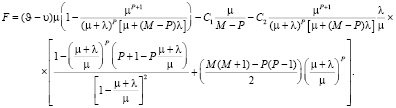 (27)
(27)
Взяв производную от F по P и приравняв результат к нулю, получим уравнение, решая которое можно найти оптимальное значение критического уровня запаса P, а по уравнению (1) – оптимальный размер заказа Q. Производную от F по P легко вычислить, например, с помощью символьного процессора пакета Mathcad (не приводится в данной работе ввиду громоздкости).
Пример. Известно, что математическое ожидание спроса на лекарственное средство составляет 200 единиц в день, а максимальный ежедневный объём запаса ЛС в аптеке не должен превышать 400 единиц. Среднее время доставки заказа составляет 6 часов или 0,5 рабочих дней. Аптека закупает лекарственное средство по цене 400 рублей за единицу, а продавать намерена за 500 рублей за единицу. Оформление одного заказа обходится аптеке в 2000 рублей, независимо от размера партии, а стоимость хранения единицы ЛС с учётом всех накладных и прочих расходов – 10 рублей в день.
Требуется определить оптимальную стратегию пополнения запасов ЛС, при которой прибыль аптеки от реализации лекарственного средства будет максимальной.
Из уравнения T = 1/λ найдём интенсивность пополнения запаса λ:
λ = 1/0,5 = 2.
Затем, для найденного λ = 2 и заданных μ = 200, M = 400, ϑ = 500, υ = 400, C1 = 2000 и C2 = 10 из уравнения производной (27) по P находим оптимальное значение P* = 134,66. Округляя значение до ближайшего целого, получаем решение задачи – 135. Таким образом, критический уровень запаса составляет 135 единиц лекарственных средств, а стратегия управления запасами будет заключаться в следующем: каждый раз, когда уровень запаса уменьшается до 135 единиц, следует заказывать 265 единиц ЛС. В этом случае вероятность 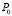 отсутствия ЛС в течение дня будет равна 0,056, средний ежедневный уровень запаса
отсутствия ЛС в течение дня будет равна 0,056, средний ежедневный уровень запаса 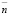 – 211 единицам, а ежедневная прибыль аптеки от реализации ЛС – 17577 рублям.
– 211 единицам, а ежедневная прибыль аптеки от реализации ЛС – 17577 рублям.
Заключение
Модель управления запасами с фиксированным размером заказа может быть использована для управления запасами в аптечных организациях. Важнейшей особенностью приведённой модели является возможность получения оптимальных параметров стратегии управления запасами при известном математическом ожидании спроса на лекарственные средства.
Библиографическая ссылка
Истомин А.Л., Бадеников А.В., Истомина А.А. МОДЕЛЬ УПРАВЛЕНИЯ ЗАПАСАМИ С ФИКСИРОВАННЫМ РАЗМЕРОМ ЗАКАЗА НА ПРИМЕРЕ ФУНКЦИОНИРОВАНИЯ АПТЕЧНЫХ ОРГАНИЗАЦИЙ // Современные наукоемкие технологии. 2018. № 4. С. 49-54;URL: https://top-technologies.ru/ru/article/view?id=36958 (дата обращения: 13.02.2026).



