Теория глобального поиска, в отличие от теории локальной оптимизации, не является завершенной и в настоящий момент проходит стадию становления. В связи с этим опубликовано весьма значительное количество сообщений о реализации различных алгоритмов: например, поисковая машина «Яндекс» по запросам, включающим ключевые слова «глобальная оптимизация», «алгоритмы мультистарта», «генетические алгоритмы», «глобальный случайный поиск», предоставляет более 15 млн ссылок только в русскоязычном сегменте глобальной сети Интернет. Однако анализ этой информации позволяет сделать вывод о недостаточном количестве систематизированного изложения основ теории поиска. В русскоязычной литературе исчерпывающий обзор глобальных методов дан в [1]. В списках русскоязычных литературных источников встречаются в среднем 2 ссылки на монографии, например [1, 2]. Причиной этого явления можно считать большую практическую значимость задачи глобального поиска в современных информационных технологиях и популярность простых с точки зрения возможности теоретического обоснования эмпирических алгоритмов, это, в частности, генетические алгоритмы и алгоритмы роя частиц [2]. Некоторые попытки классификации также предприняты авторами [3, 4]. Вместе с тем надо заметить, что математически строго обоснованные методы, изложенные, например, в монографиях [5, 6], не получили широкого распространения, в том числе из-за вычислительных ограничений, наложенных на размерность задачи.
Методологически методы глобального поиска разделены на две группы: детерминированные и эмпирические методы [1, 3]. В настоящее время предпочтение отдается практически значимым методам из второй группы, а детерминированные алгоритмы служат своего рода «моделями», которые позволяют, например, выделить свойства функции цели или оценить время исполнения алгоритма. Рассмотренный в этой статье модифицированный случайный поиск является типичным представителем второй группы методов.
Некоторые актуальные задачи требующие практического применения методов глобальной оптимизации
Одной из причин популярности методов случайного глобального поиска является качественный рост технологий искусственного интеллекта на основе нейронных сетей. Развитие различных подходов в архитектуре нейрокомпьютеров требует модификации обучающих алгоритмов. Специфика оптимизации обучения нейронной сети состоит именно в большой размерности задачи, число параметров которой может превосходить 105. Для получения удовлетворительных результатов требуемый объем памяти алгоритма должен линейно зависеть от числа параметров. Кроме этого, данная задача является многокритериальной, и окрестность определенного минимума должна быть достаточно большой. Такое условие заставляет предположить, что целевая функция оценки в окрестности глобального минимума становится «достаточно пологой». Это делает невозможным применение методов наискорейшего спуска [7, 8].
Технологии нейронных сетей, по сути, предназначены для эффективного решения задачи распознавания образов. Задачи этого класса являются приоритетными в системах специального назначения. Однако специфичность информационных систем в военной отрасли заключается не только в необходимости оперативного реагирования, надежной защиты и высокой точности обработки данных. Указанные требования в настоящее время предъявляются ко всем информационным системам. Для задач оптимизации систем специального назначения соблюдение этих требований носит императивный характер. В связи с этим в таких задачах вводятся дополнительные ограничения, усложняющие структуру множества оптимизации. По этой же причине задачи оптимизации систем специального назначения являются многокритериальными. Императивность ограничений влечет за собой жесткость модели, следовательно, неустойчивость найденного решения. Решение задачи определения многочисленных параметров системы, которая, по сути, является обратной задачей, будет весьма вариативным, независимо от математической модели системы [9].
Задача оптимизации производственной системы по экономическому критерию остается востребованной в области глобальной оптимизации. Из-за большого количества неопределенных параметров целевая функция является многоэкстремальной на множестве оптимизации. Кроме того, само множество оптимизации может иметь весьма сложную структуру, поэтому применение регулярных алгоритмов теории глобальной оптимизации невозможно [10]. Представляет теоретический и практический интерес рассмотрение вопроса о возможности модификаций представленного алгоритма в рамках схемы так называемых алгоритмов роя частиц. Заметим также, что представленный подход не теряет своей общности для решения задачи оптимизации системы специального назначения с учетом предполагаемой неустойчивости решения.
Идея модификации метода глобального поиска, снижающая вычислительные затраты при реализации алгоритма
Ниже кратко описана модификация алгоритма случайного поиска с направляющим конусом.
Применение марковских алгоритмов для поиска глобального экстремума на множестве Х функции F подробно рассмотрено в [1]. Суть метода случайного поиска с направляющим конусом состоит в следующем: компоненты случайного вектора ξк размерности m должны лежать в некотором гиперконусе K с осью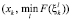 
с центром в точке xk, т.е. 
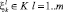. Угол раскрытия гиперконуса φ может выбираться по некоторому распределению, но в данном исследовании этот параметр выбирается эмпирически.
Все модификации случайного поиска имеют своей целью уменьшение числа траекторий за счет отсеивания «близких» поисковых последовательностей [2, 9]. Интуитивно ясно, что правило отсеивания таких траекторий конструктивно учитывает возможность неустойчивого развития процесса поиска.
Для удобства изложения назовем последовательность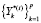 
полной траекторией поиска 
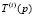, исходящей из точки 
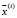, подпоследовательность этой последовательности есть частичная траектория. Точки 
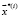назовем узлами траектории, а число узлов р – вместимостью траектории. Кроме этого, последовательность 
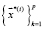назовем проекцией траектории на множество Х.
На первом этапе генерируется m случайных векторов, равномерно распределенных на множестве Х. Делается р1 шагов случайного поиска с направляющим конусом, после этого выполняется следующая процедура сравнения. Если для некоторых подпоследовательностей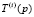 
и 
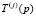выполнено 
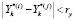, а для проекций выполнено 
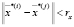, то, если 
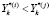, то по траектории 
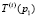дальнейший поиск не ведется. Перспективной считается траектория 
.
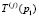Операции сравнения, произведенные не только над результатами вычисления целевой функции, но и над их проекциями на множество оптимизации позволяют выявить в рельефе поверхности поиска области «устойчивого изменения».
Если выполнено только неравенство для проекций, тогда при поиске по траектории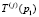 
на следующем шаге увеличивается параметр, определяющий величину окрестности очередного узла хк и угол раскрытия конуса φ, если это же неравенство выполнено для следующих n1 шагов, то траектория 
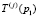отсеивается как неперспективная. Это эмпирическое правило предназначено для выявления в рельефе целевой функции областей «крутых ступеней», т.е. резких скачков значений целевой функции. Именно это правило несет в себе смысловое объединение понятия «устойчивого развития» процесса глобального поиска.
Применение глобального поиска при численном моделировании систем
Ниже рассмотрено два подхода к применению глобального случайного поиска в процессе моделирования систем. Под системой понимается совокупность n объектов, описанных математическими моделями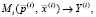 
i = 1..n, при этом существуют хотя бы (n/2 – 1) пар (i, j), таких, что 
.
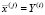Здесь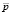 
– вектор параметров модели; 
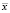– вектор влияющих факторов, 
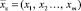. Каждая компонента этого вектора лежит в некотором промежутке варьирования Ai ≥ хi ≥ Bi.
Оптимизационную задачу можно поставить следующими способами:
- Сформулировать критерий оптимизации (один или несколько) как функцию управляющих параметров моделей [9]. Эта функция представляет собой характеристику системы «в целом». Примером служат всевозможные критерии, имеющие экономический смысл [5].
- Решать отдельные оптимизационные задачи для каждого объекта, исходя из условий его работы. В частности, для объекта, моделью которого служит динамическая система, необходимо исследовать условия устойчивости и (или) решать задачу оптимального управления этим объектом. Общий критерий оптимальности тогда мог бы представлять собой мультипликативную функцию, объединяющую критерии каждого объекта.
Оба эти подхода требуют применения алгоритмов глобальной оптимизации, во-первых, из-за большой размерности вектора управляющих параметров, во-вторых, из-за возможных множественных рециклов в графе, представляющем схему связей объектов системы. Некоторые особенности расчетов химико-технологических систем представлены в [5, 9].
В качестве тестовой рассмотрена система объектов, которые описаны дифференциальными уравнениями с нелинейными коэффициентами, отражающими предполагаемые обратные связи.
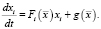
В качестве критерия оптимизации рассматривалась функция
,
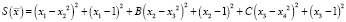представляющая собой один из вариантов функции Розенброка, являющейся тестовой для алгоритмов глобальной оптимизации.
Расчеты проводились для систем из трех или четырех объектов, эволюция которых описывается системой из уравнений с переменными коэффициентами Fi. Графы, представляющие схемы этих систем, включали рециклы (см. рисунок). Коэффициенты Fi имели вид линейных зависимостей.
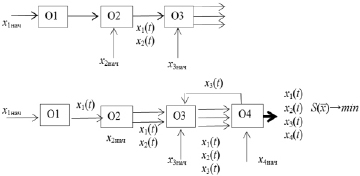
Схемы объектов, соединенных в систему
По существу, в расчетах ставилась задача оптимизации функции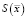 
на разбиении временного интервала в системе объектов, эволюция которых моделируется различными системами уравнений. Так, О1 рассчитывался по известной логистической модели
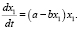
Объекты О2 и О3 по известной модели Лотка – Вольтерра. Требовалось определить такие начальные условия и такие моменты времени в развитии каждого объекта, при которых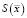 
достигает своего минимума.
Если потребовать выполнения условия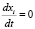 
, то задача сводится к задаче оптимизации с ограничениями типа равенств, может решаться известными методами.
Если же условие стационарности процесса не выполнено, то вычислительная задача сводится к многократному последовательному численному решению систем, таким образом, что начальные условия для второго и последующих объектов содержат в себе решения, найденные для предыдущего объекта. Количество решений задачи оптимизации, таким образом, связано с числом шагов в решении, определяющем изменение объекта, рассчитанного первым.
Таким образом, на каждой итерации поиска проводился полный расчет системы и вычисление значения критерия оптимизации. Очевидно, что объем вычислений для такой задачи весьма значителен, следовательно, параметры алгоритма оптимизации должны подбираться также очень тщательно.
В качестве алгоритма минимизации использовался рассмотренный выше метод модифицированного случайного поиска. Параметры модифицированного случайного поиска: угол раскрытия конуса φ, радиус окрестности очередного узла μ, число шагов до первого сравнения р1, а также величины Rx и Ry, определяющие близость траектории, варьировались в ходе вычислительного эксперимента. Выбор данного алгоритма обусловлен именно возможностью «отсечения» близких траекторий поиска.
Некоторые предварительные результаты и выводы
При расчете системы из трех последовательных объектов, которая является основой для расчета системы с рециклом (рисунок) в ходе оптимизации проявились следующие вычислительные проблемы:
– недостаточная точность определения минимума в ходе глобального поиска, требуется дополнительное уточнение результата локальными процедурами;
– взаимозависимость параметров μ и φ, эмпирически было определено следующее соотношение μ = 2,5k·sin(φ/2), где k = 10n;
– применение простого генетического алгоритма для сравнительного анализа не привело к существенному улучшению ни в смысле точности поиска минимума, ни в смысле времени, затраченного на минимизацию.
При дополнении системы еще одним объектом и введении рецикла выявлена необходимость увеличения числа шагов р1 поиска до сравнения траекторий при незначительном (0,5–5 %) изменении любого из начальных условий. Вместимость траектории, таким образом, увеличивается в среднем на 20 %, что является показателем довольно высокой чувствительности этого параметра. При изменении всех начальных условий в таких же пределах средняя вместимость траектории не изменяется.
Изменение параметров Rx и Ry не оказывает значительного влияния на вместимость траектории поиска, несмотря на то, что вычислительная погрешность, накапливаемая на каждом шаге, имеет значение именно при рассмотрении «близких» траекторий. Возможно, это объясняется «овражистым» рельефом целевой функции.
Заключение
Вычислительный эксперимент в рамках представленного подхода к моделированию систем является предварительным этапом в серии расчетов. Особенностью глобального поиска при проектировании систем является необходимость тщательного исследования связи структурной устойчивости объектов, составляющих систему, и поведения целевой функции. Эта задача, хотя и является алгоритмически более простой, чем известные задачи поиска оптимального управления, все же требует значительных вычислительных ресурсов. Среди алгоритмов глобальной оптимизации, объединенных методологией случайного поиска, нельзя однозначно указать наиболее эффективный подход для абсолютного большинства тестовых задач.
В целом направление исследований перспективно, поскольку является попыткой синтеза некоторых важных подходов в современном моделировании – системного анализа и глобального поиска.
Библиографическая ссылка
Певнева А.Г., Ананченко И.В. ОСОБЕННОСТИ ПРИМЕНЕНИЯ МЕТОДОВ ГЛОБАЛЬНОГО СЛУЧАЙНОГО ПОИСКА В МОДЕЛИРОВАНИИ СИСТЕМ // Современные наукоемкие технологии. – 2018. – № 3. – С. 85-89;URL: https://top-technologies.ru/ru/article/view?id=36941 (дата обращения: 21.11.2024).