В течение последних тридцати лет был совершен значительный прорыв в развитии мирового промышленного оборудования, военной техники, а также техники специального назначения. Значительное увеличение электроники, установленной на оборудовании, многократное усложнение конструкторских решений с целью повышения эффективности эксплуатации в значительной степени повысили перспективность обновления парка техники. Однако результаты деятельности эксплуатанта зависят не только от качества парка техники, но и от эффективности организации процессов материально-технического обеспечения (МТО) машиностроительной продукции на стадии эксплуатации.
Из всех задач, возлагаемых на службу МТО, можно выделить одну из ключевых – это определение потребностей во всех видах материалов и запасных частей, необходимых для эксплуатации [1]. При этом служба МТО несет ответственность и должна достигать следующих целей:
- поддержание работоспособного состояния эксплуатируемой сложной машиностроительной продукции имеющимися материалами, комплектующими и запасными частями (МКЗ) для выполнения работ по техническому обслуживанию и ремонту (ТОиР);
- обеспечение эксплуатирующих предприятий запасов МКЗ, позволяющих снизить затраты на послепродажное обслуживание имеющегося парка техники.
Решение данной задачи осуществляется путем математического моделирования, что в результате позволяет получить ответ на главные вопросы:
1. Какую номенклатуру, т.е. перечень предметов МТО, необходимо сгруппировать и закупать для поддержки эксплуатации?
2. Какой оптимальный объем МКЗ по каждому виду номенклатуры для каждого эксплуатируемого изделия необходимо заказать и хранить? (Т.е. какой объем запаса должен присутствовать в системе МТО для обеспечения надежности и эффективности эксплуатации?)
Главное требование к системе МТО – своевременно и в полном объеме удовлетворять потребность организации, эксплуатирующей продукцию, в МКЗ, в целях непрерывного ведения деятельности. Непрерывность эксплуатационного процесса позволяет наращивать объемы производства, если речь идет о машиностроительной продукции гражданского назначения.
Поскольку задачи, решаемые в системе МТО, можно отнести к логистическим вопросам, то при их решении необходимо учитывать логистические факторы, которые формализуют особенности техники и сделают возможным их учет в экономико-математических моделях [2, 3]. Способ учета факторов подробно представлен в статье «Критерий эффективности цепей поставок и построение целевой функции в задачах оптимизации материально-технического снабжения для сложной техники», написанной И.Н. Омельченко, А.Е. Бром, И.Д. Сидельниковым.
Одним из первоначальных вопросов при решении данной задачи является назначение продукции. Именно на основании данного критерия осуществляется постановка задачи и осуществляется моделирование запаса в системе МТО. Машиностроительная продукция может быть гражданского назначения или военного и специального назначения (ТВСН).
Перед службами МТО стоит проблема эффективности цепей поставок для обеспечения предприятия МКЗ. В случае, если снабжение осуществляется для техники гражданского назначения, то критерием эффективности выступают минимальные затраты на организацию МТО, при обеспечении требуемого уровня технической готовности объекта техники [4–6]. Соответственно, постановка задачи будет выглядеть следующим образом: необходимо найти оптимальные значения поставок МКЗ, при которых будут минимизироваться затраты цепей поставок и обеспечиваться требуемый уровень коэффициента технической готовности.
Осуществим формулировку задачи оптимального управления запасами для техники гражданского назначения. Данная задача представляется в многономенклатурной постановке. Рассмотрим задачу поиска оптимального объема по каждому наименованию номенклатуры. Соответственно, необходимо найти объем запаса каждого вида МКЗ на складах предприятия, обеспечивающий минимальные затраты. При этом есть ограничения, связанные с обеспечением вероятности безотказной работы изделия не ниже заданной.
Z0 > min,
P0 ≥ Pзадан,
где Pзадан – требуемый уровень надежности системы.
Суммарные затраты на обеспечение запаса зададим в форме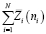 
, где 
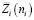– затраты на обеспечение i-го вида запасов МКЗ, причем для каждого отдельного случая функция 
имеет свой вид. В простейшем случае затраты на обеспечение запаса, как правило, прямо пропорциональны количеству резервных элементов.
Если результирующая вероятность безотказной работы системы «изделие – запас» задана величиной P0, то вероятность отказа Q0 будет равна [7]:
Q0 = 1 – P0.
При построении модели необходимо сделать следующие допущения:
1) отказы запасных элементов МКЗ в вероятностном смысле независимые друг от друга события;
2) отказ любого типа МКЗ влечет за собой отказ запаса в целом.
Для вероятности отказа QC системы с учетом принятых допущений имеем
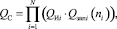(1)
где Qзапi(ni) – вероятность отказа по i-ому типу запаса МКЗ. Вероятность отказа QИi зависит от условий отказа технического устройства по элементам, которые составляют i-ый тип запаса, но QИi не зависит от числа ni запасных элементов i-го типа. Вероятности отказа QИi, i = 1,…..,N, в вероятностном смысле независимы друг от друга, и каждую вероятность отказа QИi на практике можно рассчитать, исходя из условий отказа, методами теории вероятностей [8, 9]. В нашем случае будем считать QИi известной постоянной величиной для каждого порядкового номера вида МКЗ.
Для решения поставленной задачи воспользуемся методом неопределенных множителей Лагранжа [10].
Введем функцию Лагранжа, отражающую особенности рассматриваемой системы:
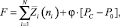(2)
где φ – неопределенный множитель Лагранжа.
Перепишем выражение в правой части в квадратных скобках функции Лагранжа с учетом заданных величин:
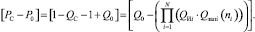
Теперь окончательно функция Лагранжа принимает вид:
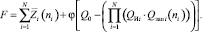(3)
Воспользуемся известным, достаточно эффективным и широко применяемым в экономической теории предположением, что величины ni достаточно велики, тогда можно считать, что функция F является непрерывной (более строго, дифференцируемой) функцией своих аргументов. Это позволяет продифференцировать соотношение (3) по переменным ni и φ, а получившийся результат приравнять к нулю – обеспечение необходимого условия экстремума функции Лагранжа.
На основе метода множителей Лагранжа можно получить достаточные условия условного экстремума, требующие анализа (в простейшем случае) вторых производных функции Лагранжа F. Предполагаем, что достаточные условия экстремума выполнимы.
C учетом выражения для функции Лагранжа после дифференцирования эта система уравнений принимает вид
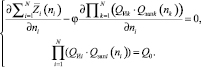(4)
Взятие производной в первом члене первого уравнения системы (4) трудностей не вызывает для соответствующего вида заданной функции затрат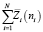 
, а вот вычисление частных производных по каждому аргументу от произведения N независимых функций, если каждая из них является только функцией «своего» аргумента.
Представим произведение N независимых функций, каждая из которых является только функцией «своего» аргумента:
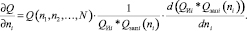
Тогда для второго члена первого уравнения системы (4) получим
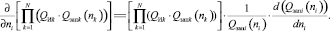
После нахождения производных первое уравнение системы (4) принимает вид
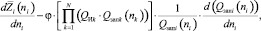(5)
а второе уравнение системы (уравнение связи) запишем в форме
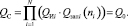
Из соотношения (5) получим выражение для множителя Лагранжа φ:
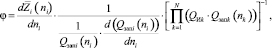(6)
откуда следует, что выражение (6) для определения φ справедливо для всех значений i (по условиям метода неопределенных множителей Лагранжа)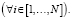 
Заметим, что последний сомножитель в правой части соотношения (6) не зависит от индекса i, это интегрированная величина, одна и та же для всех конкретных i в уравнениях Лагранжа, тогда введем новое определение неопределенного множителя Лагранжа:
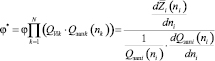, (7)
φ* – аналогично φ рассчитывается одинаково для всех i, т.е. не меняется при переходе от соотношения с одним индексом к соотношению с другим индексом.
Из соотношения (7) следует
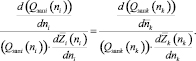(8)
Выберем произвольную величину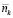 
и заметим, что индекс k выбран хоть и произвольно, но фиксировано из совокупности переменных (n1, n2,…, N). Положим k = 1 и тогда выбранным базовым типом МКЗ будет первый тип с числом запасных элементов n1. Соотношение (8) связывает между собой значение n1 с выбранным значением 
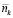. Особенность разработанного подхода состоит в том, что правая часть выражения (8) является известной функцией переменной 
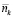, а левая – переменной ni (i = 2, …, N), откуда следует реальная возможность связать число элементов каждого типа с числом элементов выбранного конкретного типа, у нас – с числом элементов первого типа.
Соотношение (8) можно записать в виде
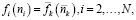
но так как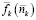 
известная функция, то можно решить это уравнение относительно ni как функции числа элементов n1 первого типа:
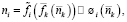(9)
где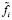 
– функция, обратная к fi(ni).
Вопросы о существовании, непрерывности обратной функции в данной статье не обсуждаются – подразумевается, что они решаются при практических расчетах.
Аналитическое решение уравнений (9) возможно в исключительных случаях, как правило, малопригодных для практического использования. Современное состояние вычислительной математики и вычислительной техники обеспечивает эффективное решение уравнений (9).
Обычно при практических расчетах значения членов последовательности ni (i = 2, …, N) получаются дробными. В этом случае следует округлить найденные значения до ближайшего целого числа.
Далее по уравнению связи (второе уравнение системы (4)) с учётом очевидного соотношения между результирующей вероятностью PС безотказной работы системы и вероятностью QС отказа системы: PС = 1 – QС, можно найти число элементов первого типа n1.
Для этого по соотношению (2.1) построим зависимость для вероятности отказа QС системы:
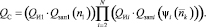
При этом предполагается, что значения вероятности отказа изделия QИi по всем i-ым типам элементов заранее рассчитаны на основе статистических данных, собранных в предыдущие периоды и, очевидно, не зависящих от количества запасных элементов МКЗ.
Полученное уравнение алгебраическое, может оказаться трансцендентным (решение может быть не единственным), но современная вычислительная математика и вычислительная техника предлагают много методов для решения подобных уравнений: метод последовательного приближения, метод касательных, метод секущих, графический метод и другие. Их возможности, достоинства и недостатки хорошо известны.
Полученная зависимость QС зависит только от одного-единственного числа n1 элементов выбранного типа, остальные величины – известные параметры задачи.
Проиллюстрируем, например, графический способ нахождения числа, запас элементов выбранного типа n1, он является очень наглядным (см. рисунок). При заданных зависимостях QИi и Qзапi(ni) можно построить график зависимости PС = 1 – QС, где аргумент при использовании непрерывного подхода будет откладываться на числовой оси от 1 в положительном направлении.
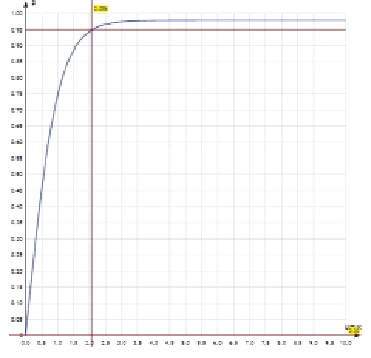
Графический способ нахождения решения
На этом же графике проводится линия требуемой вероятности Р0 работоспособности системы в целом. Пересечение этих линий определяет величину n1 числа запасных элементов выбранного типа. После этого рассчитываются величины чисел элементов всех остальных типов по соотношению (9) с округлением до ближайшего целого числа (переход к дискретным величинам), а также сумма затрат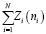 
.
Если аналитическое решение уравнений (9) получить не удаётся, приходится задавать интуитивно разумную последовательность возможных значений числа запаса элементов (например, на основании статистических данных о распределении отказов рассматриваемого типа элементов) конкретного типа, выбранного «базовым»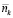 
и для каждого значения 
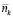вычислять совокупность значений 
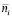для запаса всех остальных типов МКЗ. В этом случае оказывается возможным вычислить результирующую вероятность отказа системы «изделие + запас МКЗ» для каждого элемента выбранной последовательности 
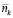и сравнить получаемый результат с заданным условием работоспособности рассматриваемой системы.
Таким образом, используя предложенный подход, будет найден оптимальный объем запаса по каждому из видов МКЗ. Стоит отметить основные достоинства предложенной модели: во-первых, данная модель открывает возможность применения любой функции, описывающей затраты в системе МТО, это подтверждает ее высокую универсальность; во-вторых, при решении задачи можно учитывать структурную избыточность машиностроительной продукции, а также задавать различные условия выхода из строя рассматриваемой системы.
Все вышеизложенное позволяет сделать вывод, что предложенная модель может быть внедрена при организации МТО для машиностроительной продукции гражданского назначения, обеспечивая экономическую эффективность процессов ремонтного обслуживания и материального снабжения, при соблюдении требований к надежности техники.
Библиографическая ссылка
Бром А.Е., Сидельников И.Д. ОПТИМИЗАЦИЯ МНОГОНОМЕНКЛАТУРНОГО ЗАПАСА В СИСТЕМАХ МАТЕРИАЛЬНО-ТЕХНИЧЕСКОГО ОБЕСПЕЧЕНИЯ МАШИНОСТРОИТЕЛЬНОЙ ПРОДУКЦИИ ГРАЖДАНСКОГО НАЗНАЧЕНИЯ // Современные наукоемкие технологии. – 2018. – № 3. – С. 19-24;URL: https://top-technologies.ru/ru/article/view?id=36930 (дата обращения: 21.11.2024).