В настоящее время изучение процесса измельчения базируется в основном на экспериментальных исследованиях, приоритетными направлениями которых являются [1, 2]:
- изучение физико-механических процессов, происходящих при разрушении твердых тел под действием внешней нагрузки;
- установление взаимосвязи между дисперсностью материала, которому присущи определенные физико-химические свойства, и затратами энергии, необходимыми для преодоления внутренних сил сцепления в материале при его разрушении;
- изучение закономерностей распределения зернового состава продуктов помола.
Изучению энергоэффективности способов трансформации энергии при формировании разрушающего усилия материала и анализу балансовых уравнений энергопотребления не уделяется достаточного внимания. Между тем, несмотря на многообразие конструктивных форм мельниц, основным фактором, предопределяющим энергоемкость производимой продукции, является способ трансформации подведенной к измельчаемому материалу энергии. При этом одним из приоритетных показателей эффективности работы измельчителей, их типа и конструкции является критерий работы по степени селективности диспергирования [3].
В понятие «селективность» (от лат. selektio – выбор, отбор, избирательность) измельчения принято включать явление, при котором не все частицы сыпучего материала, находящегося в рабочем пространстве машины, подвергаются разрушению, в этом и проявляется избирательность процесса. Такая селективность является причиной того, что дезинтеграция твердых тел – это процесс, сопровождающийся значительными потерями энергии рабочих органов на трение, деформацию материала и пр. При этом известно, что КПД процесса дезинтеграции составляет менее 1 %, так как полезной считается энергия, затраченная на образование новых поверхностей перерабатываемого материала. При единичном воздействии разрушается лишь некоторая доля частиц [4]. Повышение показателя селективности в измельчителях, в том числе и в электромагнитных механоактиваторах, является актуальной задачей современных технологий переработки материалов различного целевого назначения.
Цель исследования
Повышение показателя селективности электромагнитных механоактиваторов путем внедрения в проектный расчет результатов исследований физико-механических процессов в контактных системах «ферротела магнитоожиженного слоя – частицы перерабатываемого материала».
Материалы и методы исследования
Изучение контактных взаимодействий ферротел в электромагнитных механоактиваторах с измельчаемым продуктом с использованием физико-механических моделей электродинамики, теории упругости и механики разрушения твердых тел.
Результаты исследования и их обсуждение
Показатель селективности измельчения зависит от целого комплекса факторов. К ним относится:
- способ нагружения материала (удар, истирание и т.д.),
- скорость и кпд трансформации энергии в энергию разрушения материала,
- тонина помола сырья,
- физико-механические и реологические свойства перерабатываемого продукта.
Можно утверждать, что одним из основных факторов, предопределяющих повышение показателя селективности процесса измельчения в электромагнитных механоактиваторах (ЭММА) [5], является адекватное реальным процессам моделирование разрушения твердого тела (измельчаемого материала), априори имеющего микро- и макротрещины.
Исследования физико-механических процессов в магнитоожиженном слое ферротел ЭММА показали, что продукт, находящийся в рабочем объеме аппарата, испытывает со стороны рабочих органов энергонапряженные многоточечные воздействия ударно-истирающего характера (рисунок).
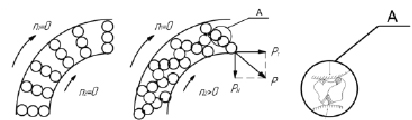
а б в
Схема формирования силового (разрушающего) усилия частиц продукта в магнитоожиженном слое ферротел ЭММА: а – формирование силовых взаимодействий между рабочими органами при неподвижных поверхностях рабочего объема (n1, n2 – частота смещения поверхностей рабочего объема); б – формирование ударно-истирающих воздействий по частицам обрабатываемого продукта при смещении поверхностей рабочего объема (Pτ, PN – тангенциальная и нормальная составляющие силовых контактов между ферротелами); в – cхема распределения трещин в частице продукта неправильной формы
Силовое взаимодействие осуществляется через прослойку обрабатываемого продукта. С учетом исходного размера частиц rЧ силы Fr и моменты Mυ, действующие на размольные элементы в рабочем объеме ЭММА, определяются равенствами
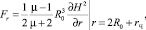(1)
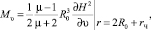(2)
где μ – магнитная проницаемость; R0 – радиус ферротел; H – напряженность магнитного поля.
Численное интегрирование дает следующие выражения:
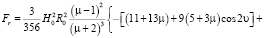
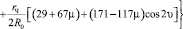, (3)
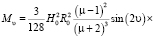
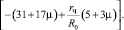(4)
При этом критический угол υКР , при котором притяжение ферротел в их магнитоожиженном слое сменяется их отталкиванием, определено по выражению
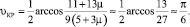(5)
В основу моделирования разрушения частицы в магнитоожиженном слое ферротел положено предположение, что существует определенная зависимость сил сцепления от расстояния в устье трещины (дефекта структуры перерабатываемого материала), т.е. промежутка между берегами трещины. Если это расстояние δк меньше некоторой постоянной величины, являющейся константой для данного материала, то силы притяжения между берегами также будут равны постоянной величине δ0. В случае, если фактическое расстояние между берегами больше δк, то δ0 = 0. Эта концепция означает, что трещина будет расти, если выполняется условие
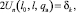(6)
где Un – нормальная составляющая вектора смещений точек берегов трещины; l0 – характерный линейный размер области начальной трещины; l – фактический размер трещины; qв – параметр, зависящий от внешней нагрузки.
При моделировании измельчаемой среды в ЭММА для описания процесса разрушения частиц материала использованы методы математической статистики. Модель квазиизотропного тела представлена однофазной системой, в объеме Wν которого частицы связаны силами сцепления. Величина Wν должна быть такой, чтобы условно считалась однородной. Внутри этого объема имеется малый объем V, существенно меньше всего тела, но имеющий достаточное количество элементарных частиц, т.е. Wν >> V.
В теории трещинообразования выделяют различные условия нагружения твердого тела, чтобы образовались микротрещины и макротрещины. Первые образуются под действием растягивающих напряжений и, даже в случае сложного напряженного состояния, рассматривается только нормальная составляющая напряжений растяжения.
Процесс макроскопических разрушений в масштабе V-объемов начинается при напряжениях меньше сопротивления разрушению поликристаллов. Относительное число разрушенных объемов V, где микротрещины возникли под действием одноосного растягивающего напряжения, равно
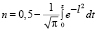, (7)
где z равно
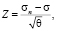(8)
где σn – среднее сопротивление разрушению кристаллов поликристаллического тела;
θ – модуль нормального распределения объемов V по напряжениям.
С увеличением внешней нагрузки число разрозненных микротрещин возрастает и, после достижения некоторой критической величины nkp, они начинают сливаться в единые, в том числе и пересекающиеся, образуя макроскопическую трещину во всем объеме Wν. Условием достижения критического числа микротрещин при любом напряженном состоянии тела является равенство
n = nkp, (9)
где kp – постоянная для данного материала величина, равная относительному числу трещин в объемах V, достаточному для макроскопического разрушения тела объемом Wν.
Твердый материал, как известно, при разрушении может вести себя хрупко или пластично. Макроскопическим разрушением обычно охвачены не все объемы Wν, а только их некоторая часть. Для более хрупкого материала эта часть меньше, поскольку в хрупком материале микротрещины опаснее, чем в пластическом. В процессе макроскопического разрушения в малых объемах V разрушение может быть вязким, а соотношение объемов Vi между хрупким и вязким разрушением определяется характером макроскопического разрушения.
Из этого следует, что в общем случае под действием внешних усилий в разрушаемом теле возникают как упругие, так и пластические деформации. Из общего числа N объемов типа V часть их Nуn – деформируется упруго, a Nпл – пластично. Общее число микротрещин к моменту макроскопического разрушения составит
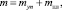(10)
где myn и mпл – число микротрещин при упругом и пластическом деформированных объемах соответственно Vуn и Vпл.
Относительное число микротрещин составит
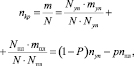(11)
где Nуn / N = p – вероятность пластического состояния;
nуn и nпл – относительное число микротрещин в пластически и упруго деформированных объемах V соответственно.
Критериями хрупкого и вязкого разрушения статистической теории прочности являются условия: nkp = nуn – хрупкое разрушение, nkp = nпл – вязкое разрушение. При этом хрупкость материала зависит от скорости приложения нагрузки и физико-механических свойств материала.
Механизм образования трещин при разрушении малых частиц имеет свои особенности. Для объяснения временной прочности твердых тел привлекаются обычно в той или иной форме представления Гриффитса о зародышевых трещинах. Значение фактической прочности с учетом наличия в теле некоторой чечевицеобразной «опасной» трещины длиной lm равно
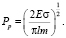(12)
При P > Pp трещина растет и тело разрушается, при P < Pp трещина смыкается и исчезает. Размер опасных трещин согласно теории Гриффитса определяется отношением
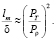(13)
Как показывает практика, средние размеры частиц могут быть и меньше «опасных» трещин. В этом случае модель Гриффитса должна быть дополнена учетом конечных размеров тела. Если в кубе со стороной X внешней силой F созданы упругие напряжения и образовалась трещина размером l, то работа внешней силы F на ее образование равна
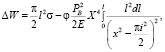(14)
где Pв – напряжение, создаваемое внешней силой, σ – полная работа создания единицы поверхности, распространяющей трещины, φ – численный коэффициент, учитывающий наклон плоскости наибольших напряжений к направлению внешней силы.
Из условия устойчивости трещины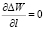 
следует
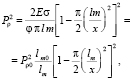(15)
где Pp0 и lm0 – разрушающее напряжение и длина опасных трещин массивных образцов.
Если считать уровень разрушающих напряжений массивных и малых объектов одинаковым, т.е. положить Pp0 = Pp, то для зависимости lm(X) получается выражение
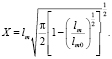(16)
В случае разрушения сжатием механически твердых тел возможные направления распространения трещины ограничены малыми углами θ, т.е. трещины будут развиваться вблизи области пластического деформирования (рисунок, в).
Заключение
Выявлено, что наиболее вероятным местом зарождения опасных трещин являются поверхностные слои на границе соприкосновения разрушаемой частицы с ферротелами магнитоожиженного слоя в процессах их контактного ударно-истирающего взаимодействия.
Вблизи поверхности сосредоточено основное количество дефектов, облегчающих образование трещин, а на границе контакта – наибольшее напряжение.
Моделирование процесса разрушения материалов с образованием «опасных трещин» позволяет проектировать электромагнитные механоактиваторы с высоким прогнозируемым показателем селективности разрушения.
Библиографическая ссылка
Беззубцева М.М., Волков В.С. К ВОПРОСУ ИЗУЧЕНИЯ КОНТАКТНЫХ ВЗАИМОДЕЙСТВИЙ ФЕРРОТЕЛ В ЭЛЕКТРОМАГНИТНЫХ МЕХАНОАКТИВАТОРАХ С ИЗМЕЛЬЧАЕМЫМ ПРОДУКТОМ // Современные наукоемкие технологии. – 2018. – № 3. – С. 14-18;URL: https://top-technologies.ru/ru/article/view?id=36929 (дата обращения: 21.11.2024).