Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Гиш Т.А. 2 Белов С.П. 1 Калмыков И.А. 2 Дунин А.В. 2 Ефимович А.В. 2 Калмыков М.И. 2

---

1 ФГАОУ ВО «Белгородский государственный национальный исследовательский университет» (НИУ «БелГУ»)

2 ФГАОУ ВО «Северо-Кавказский федеральный университет»

В работе представлена математическая модель выполнения дискретного вейвлет-преобразования с использованием модулярных кодов. Целью исследований является повышение точности и скорости выполнения кратномасштабного анализа сигналов. Одним из наиболее перспективных направлений использования дискретных вейвлет-преобразований являются системы передачи, использующие ортогональное частотное мультиплексирование. В модулярных кодах целые числа представляются в виде наборов остатков, которые получены путем деления на взаимно простые основания, которые являются модулями непозиционного кода. Параллельная обработка малоразрядных остатков по основаниям кода системы остаточных классов позволяет повысить скорость вычисления. При этом отсутствие обмена данных между основаниями кода системы остаточных классов также способствует снижению временных затрат на проводимые вычисления. Представление коэффициентов Добеши в виде целочисленных значений позволит также повысить точность выполняемых вейвлет-преобразований. Таким образом, применение новых модулярных технологий, в частности кодов системы остаточных классов, в задачах цифровой обработки сигналов позволяет за счет распараллеливания на уровне операций и обработки малоразрядных данных не только увеличить точность вычислений, но и снизить временные затраты на проводимые вейвлет-преобразования.

Статья в формате PDF

597 KB

дискретное вейвлет-преобразование

кратномасштабный анализ сигналов

модулярный код

система остаточных классов

точность

реальный масштаб времени

1. Калмыков И.А., Дунин А.В., Гиш Т.А. Реализация крупномасштабного анализа сигналов с использованием непозиционных кодов классов вычетов // Современная наука и инновации. – 2016. – № 4. – С. 67–75.

2. Червяков Н.И., Ляхов П.А. Реализация модулярного вейвлет-преобразования в нейросетевом базисе // Нейрокомпьютеры: разработка, применение. – 2011. – № 11. – С. 18–25.

3. Grinsted A., Moore J.C., Jevrejeva S. Application of the cross wavelet transform and wavelet coherence to geophysical time series // Nonlin. Processes Geophys. – 2014. – № 11. – Р. 561–566.

4. Hans-Georg Stark Wavelets and signal processing // Springer International Publishing Switzerland. – 2005. – 254 р.

5. Червяков Н.И., Коляда А.А., Ляхов П.А. Модулярная арифметика и ее приложения в инфокоммуникационных технологиях / Н.И. Червяков, А.А. Коляда, П.А. Ляхов. – М.: ФИЗМАТЛИТ, 2017. – 400 с.

6. Ananda Mohan Residue Number Systems. Theory and Applications // Springer International Publishing Switzerland. – 2016. – 351 р.

7. Amir Sabbagh Molahosseini Embedded Systems Design with Special Arithmetic and Number Systems // Springer International Publishing AG. – 2017. – 390 р.

8. Omondi A. and Premkumar B. Residue Number Systems: Theory and Implementation // Imperial College Press. UK. – 2007. – 296 р.

9. Katkov K.A., Timoshenko L.I., Kalmykov I.A., Dunin A.V., Gish T.A. Application of Modular Technologies in the Large-Scale Analysis of Signals // Journal of Theoretical and Applied Information Technology. – 2015. – № 80(3). –

Р. 391–400.

10. Шоберг А.Г. Современные методы обработки изображений: модифицированное вейвлет-преобразование / А.Г. Шоберг. – Хабаровск: Изд-во Тихоокеан. гос. ун-та, 2014. – 125 с.

В настоящее время при решении задач цифровой обработки сигналов (ЦОС), связанных с обработкой и сжатием сигналов, все чаще стали применяться дискретные вейвлет-преобразования (ДВП) [1–4]. Кратномасштабная теория, которая положена в ДВП, позволяет провести представление и анализ сигналов при различных разрешениях. Повысить точность и скорость проведения кратномасштабного анализа сигналов можно за счет использования модулярных кодов, в частности, системы остаточных классов (СОК). В работах [5–8] показано, что коды СОК эффективно выполняют арифметические операции сложения, вычитания и умножения по модулю. Следовательно, применение целочисленной модулярной арифметики позволит повысить эффективность выполнения ДВП, так как операции сложения, вычитания и умножения положены в основу кратномасштабного анализа сигналов. Поэтому реализация ДВП сигналов с использованием кодов СОК является актуальной задачей.

Цель исследования

Использование целочисленной арифметики позволяет повысить точность выполнения ДВП сигналов. Так в работе [9] представлен метод выполнения ДВП Хаара с использованием GF(p), что позволило заменить коэффициенты ДВП целочисленными значениями. В результате была достигнута максимальная точность реализации ДВП сигнала.

Однако увеличение разрядности обрабатываемых дискретных отсчетов сигнала приводит к значительному увеличению значения модуля р, а значит, и схемных затрат. Устранить данный недостаток можно за счет применения модулярных кодов СОК. Поэтому целью работы является повышение точности и скорости выполнения ДВП за счет использования модулярных кодов.

Материалы и методы исследования

Модулярный код системы остаточных классов в качестве оснований использует взаимно простые числа рi, i = 1, 2, …, k. В этом случае число А задается набором остатков, полученных при делении А на модули mi, в виде

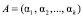, (1)

где 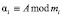; i = 1, 2, …, k.

Применяя изоморфизм, порожденный китайской теоремой об остатках (КТО), коды СОК позволяют операции над операндами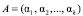
и 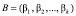 представить в виде

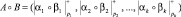, (2)

где  – операции сложения, вычитания и умножения по модулю.

Произведение оснований кода СОК определяет рабочий диапазон

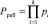. (3)

Для получения правильного результата должно выполняться .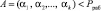

Так как вычисления в СОК выполняются параллельно и независимо по модулям кода над малоразрядными остатками, то это позволяет повысить скорость выполнения вычислений задач ЦОС [5, 7, 10]. В работах [8, 10] показано, что основу кратномасштабного анализа сигналов составляют операции сложения, вычитания и умножения

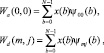(4)

где X = [x(0), x(1),…, x(N – 1)] – входной вектор; 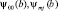 – скалинг-функции ДВП; Wa(0,0) и Wd(m, j) – аппроксимирующие и детализирующие последовательности.

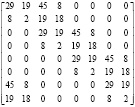
В настоящее время широкое применение нашли дискретные вейвлет-преобразования Добеши. Это обусловлено их достоинствами, приведенными в работах [3, 4]. Рассмотрим выполнение ДВП Добеши (Db4). Пусть обработке подвергается входной вектор, содержащий 8 точек. Тогда матрица для выполнения ДВП Добеши-4 примет следующий вид:

, (5)

где ; ; ; .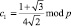

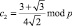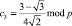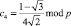Очевидно, что конечных полей Галуа GF (р), позволяющих реализовать целочисленное дискретное вейвлет-преобразование Добеши, существует множество. Это может стать основой для перехода от одномерного кратномасштабного анализа Добеши к многократному. В этом случае справедливо

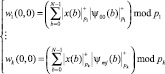, (6)

где 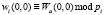; i = 1, 2, …, k.

Значение детализирующей последовательности будет иметь вид

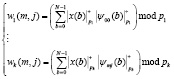, (7)

где 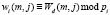; i = 1, 2, …, k.

При этом требования, которые предъявляются к дискретному вейвлет-преобразованию Добеши, будут выполняться в полной мере

; ;

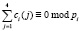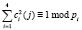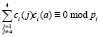. (8)

Очевидно, что аппроксимирующие и детализирующие последовательности Wa(0,0) и Wd(m, j) представлены в виде наборов остатков по основаниям СОК. Преобразуем полученный результат в позиционный код, используя китайскую теорему об остатках (КТО). Тогда

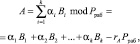(9)

где Bi – ортогональные базисы кода СОК; rA – ранг числа, показывающий количество превышений рабочего диапазона.

Результаты исследования и их обсуждение

Рассмотрим реализацию ДВП Добеши в коде СОК, в котором выбраны основания р1 = 23, р2 = 47, р3 = 71. Вычислим коэффициенты Добеши по модулю р1 = 23. Получаем 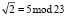, 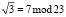. Тогда имеем ; ; ; .

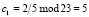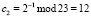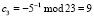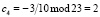Вычислим коэффициенты Добеши по модулю р2 = 47. Получаем 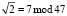, 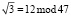. Тогда коэффициенты равны ; ;
; .

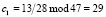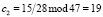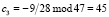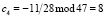Вычислим коэффициенты Добеши по модулю р3 = 71. Получаем 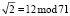, 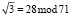. Тогда коэффициенты равны ; ; ; .

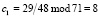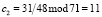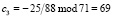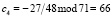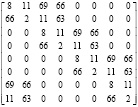
Тогда матрицы для проведения ДВП Добеши-4 в коде СОК имеют вид

Пусть необходимо провести кратномасштабный анализ сигнала, входной вектор которого равен x(n) = {7, 2, 5, 17, 6, 11, 2, 18}. Для этого вычислим произведение данного вектора на матрицу Добеши по модулю р1 = 23. В результате получаем

.

Реализация ДВП Добеши по модулю р1 = 23 позволила получить разложение сигнала 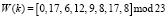. Тогда сглаживающие коэффициенты ДВП определяются свертками входного сигнала, которые получены с помощью первой, третьей, пятой и седьмой строк матрицы, т.е. 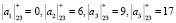. Данные коэффициенты можно вычислить, используя низкочастотный фильтр Н. При этом детализирующие коэффициенты представляют собой свертки входного сигнала со второй, четвертой, шестой и восьмой строками матрицы, т.е. 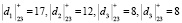. Данные коэффициенты можно вычислить, используя высокочастотный фильтр G. Тогда исходный сигнал имеет вид

,

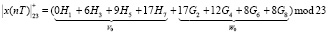где Hi – коэффициенты НЧ-фильтра; Gi – коэффициенты ВЧ-фильтра; i – номер строки матрицы ДВП Добеши.

Проведем кратномасштабный анализ входного сигнала по модулю р2 = 47. Получаем

.

Реализация дискретного вейвлет-преобразования Добеши по модулю р2 = 47 позволила получить разложение сигнала в базисе .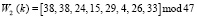

Вычислим дискретное вейвлет-преобразование Добеши по модулю р3 = 71. Тогда

.

Реализация дискретного вейвлет-преобразования Добеши по модулю р3 = 71 позволила получить разложение сигнала в базисе .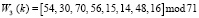

В результате выполнения дискретного вейвлет-преобразования Добеши в системе остаточных классов были получены следующие значения

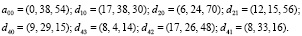
Так как результат прямого ДВП представлен в коде СОК, то его необходимо перевести в позиционную систему счисления (ПСС), используя равенство (9). Для этого необходимо вычислить ортогональные базисы для заданной системы оснований СОК. Воспользуемся алгоритмом вычисления ортогональных базисов, приведенным в работе [2].

Для вычисления ортогонального базиса В1 определим .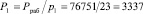
Вычислим 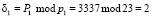. Определим значение веса В1 из условия 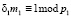. Получаем m1 = 12. Тогда ортогональный базис равен .

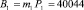Для вычисления второго ортогонального базиса определим .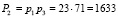
2. Вычислим 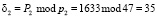. Определим значение веса В2 из условия 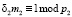. Получаем m2 = 43. Тогда ортогональный базис равен .

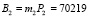Для вычисления третьего ортогонального базиса кода СОК определим значение 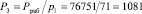. Вычислим 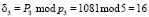. Определим значение веса В3 из условия 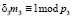. Получаем m3 = 40. Тогда ортогональный базис равен .

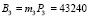Произведем обратное преобразование из модулярного кода а00 = (0, 38, 54) в позиционный код. Воспользуемся равенством (9). В результате получаем

.

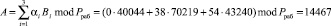Тогда разложение входного сигнала в базисе Добеши, представленном в коде СОК, будет равен W = {14467, 41210, 40256, 40952, 52058, 55323, 56990, 59159}. Очевидно, что использование кодов СОК позволяет повысить скорость выполнения ДВП. Так набор модулей СОК позволяет обеспечить обработку 16-разрядных данных, так как 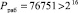. При этом максимальная разрядность остатка по модулю р3 = 71 составляет 7 разрядов. Известно, что временные затраты на выполнение операции умножения пропорциональны разрядности операндов. Таким образом, снижение разрядности обрабатываемых данных в СОК позволило сократить временные затраты на выполнение ДВП Добеши в 2,29 раза без учета выполнения операций прямого ПСС-СОК и обратного СОК-ПСС преобразований, обеспечивая при этом максимальную точность вычислений.

Заключение

В статье представлена разработанная математическая модель выполнения дискретного вейвлет-преобразования Добеши с использованием модулярных кодов. Представление сглаживающих и детализирующих коэффициентов Добеши в виде целочисленных остатков позволяет обеспечить максимальную точность выполнения ДВП. Применение кодов СОК позволяет повысить скорость вычисления дискретного вейвлет-преобразования за счет параллельной обработки малоразрядных остатков. Такое распараллеливание вычислений на уровне арифметических операций позволяет повысить скорость обработки сигналов. Так, уже при обработке 16-разрядных данных использование трех оснований СОК р1 = 23, р2 = 47, р3 = 71 позволило сократить временные затраты на выполнение ДВП Добеши в 2,29 раза по сравнению с ПСС без учета выполнения прямого и обратного преобразований. Очевидно, что при увеличении разрядности обрабатываемых отсчетов эффективность использования разработанной математической модели выполнения ДВП Добеши-4 в коде СОК увеличивается.

Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 17-37-50009.

Библиографическая ссылка