Сахарный диабет 1 типа (СД1) – это хроническое заболевание, которое характеризуется абсолютным дефицитом гормона инсулина, что обусловлено нарушением работы поджелудочной железы. Инсулин регулирует уровень содержания сахара в крови. Из-за его отсутствия в организме пациенты с СД1 вынуждены самостоятельно вводить его под кожу всю жизнь. Кроме интенсивной инсулинотерапии пациентам следует держать уровень глюкозы в норме, так как отсутствие контроля глюкозы в крови приводит к многочисленным быстропрогрессирующим сосудистым осложнениям, а в том числе и к гипер- и гипогликемической коме. Длительный мониторинг уровня сахара в совокупности с накоплением данных об инъекциях инсулина, количестве потребляемых углеводов, физических нагрузках и состоянии пациента с помощью существующих устройств контроля обеспечивают наиболее полную информацию о частоте, величине, продолжительности, направлении и причинах изменений глюкозы в крови в течение суток, позволяя более точно оценивать степень компенсации углеводного обмена и рационально корректировать терапию. Для предотвращения опасных для здоровья пациента ситуаций необходимо заранее предсказывать экстремальные значения гликемии. При прогнозировании гликемии используются различные алгоритмы машинного обучения [1, 2]. В данной статье рассматривается прогнозирование уровня глюкозы в крови с помощью искусственной нейронной сети.
Большое количество исследований показали, что нейросетевые технологии имеют высокую востребованность и широкое практическое применение в решении медицинских задач [3]. К ним относятся задачи диагностики, прогнозирования и поддержки принятия решений. Математические модели на основе нейронных сетей осуществляют прогнозирование посредством обобщения и выделения скрытых зависимостей между входными и выходными данными [4]. После обучения нейронная сеть предсказывает будущее значение определённой последовательности на основе ряда предыдущих значений и (или) каких-либо существующих в данный момент факторов. На вход нейронной сети можно подавать значения глюкозы, измеренные ранее, количество инсулина, а также количество употребляемых хлебных единиц. На выходе нейронной сети получают концентрацию глюкозы пациента, которая предсказывается с использованием перечисленных входных данных. Однако набор входных данных может различаться [5]. На вход также можно подавать параметры физической активности, стресса, показатели анализа крови и другие возрастные показатели.
Подготовка исходных данных для исследования
В связи с тем, что получение доступа к данным реальных пациентов с диабетом, использующих устройства длительного мониторинга глюкозы, оказалось затруднительной задачей, подготовка исходных данных для исследования была проведена с использованием свободно распространяемого симулятора диабетических данных AIDA (Automated Insulin Dosage Advisor). AIDA – это математическая модель, которая описывает взаимодействие глюкозы и инсулина в течение 24-часового периода с учетом чувствительности к инсулину, а также распределения глюкозы и инсулина в организме человека с сахарным диабетом 1 типа. Использование такой модели позволяет быстро собирать большое количество тестовых данных измерений уровня глюкозы в крови. В модели AIDA учитываются следующие параметры: потребление углеводов, количество и тип введенного инсулина, активность почек и степень чувствительности организма пациента к инсулину. Используя эти переменные, модель химико-биологических взаимодействий внутри организма описывается рядом уравнений для построения адекватной картины колебания уровня глюкозы в крови в течение 24-часового периода с шагом времени 0,25 ч.
Первоначально данная модель разрабатывалась для прогнозирования уровня глюкозы в крови и регулирования инсулинотерапии. Такой подход имеет ряд упрощающих предположений, при этом авторы вносят некоторые разъяснения. Например, в модель не были включены изменения гломерулярного клиренса глюкозы, которые происходят с возрастом, а также эффекты выделения контррегуляторных гормонов (глюкагона) при низких значениях уровня глюкозы в крови. Модель также предполагает, что эффекты физической активности и стресса остаются относительно постоянными во время периода моделирования. Однако данные факторы могут иметь воздействия на уровень глюкозы в крови и должны быть включены в будущие наборы данных, которые будут использоваться для обучения искусственной нейронной сети. Несмотря на эти ограничения, математическая модель AIDA является полезным исследовательским инструментом, который применяется широким кругом исследовательских групп для сбора симулированных данных об уровне глюкозы в крови для исследовательских целей [6].
При проведении исследования на основе данных AIDA была подготовлена выборка данных объемом 3000 элементов для одного пациента с сахарным диабетом 1 типа, произведенные в течение 30-дневного периода (таблица).
Фрагмент набора данных для прогноза гликемии
|
Время (ч:мин) |
Уровень гликемии (ммоль/л) |
Приём пищи (гр.) |
Короткий (ед.) |
Базальный (ед.) |
Прогноз (ммоль/л) |
|
7:00 |
3,2 |
0 |
0 |
0 |
3,2 |
|
7:15 |
3,2 |
0 |
0 |
0 |
3,2 |
|
7:30 |
3,2 |
0 |
0 |
0 |
3,2 |
|
7:45 |
3,2 |
0 |
8 |
1 |
3,3 |
|
8:00 |
3,3 |
48 |
0 |
0 |
3,3 |
|
8:15 |
3,3 |
0 |
0 |
0 |
3,1 |
|
8:30 |
3,1 |
0 |
0 |
0 |
3,2 |
|
8:45 |
3,2 |
0 |
0 |
0 |
3,1 |
|
9:00 |
3,1 |
0 |
0 |
0 |
3,2 |
|
9:15 |
3,2 |
0 |
0 |
0 |
2,9 |
|
9:30 |
2,9 |
0 |
0 |
0 |
3,6 |
|
9:45 |
3,6 |
0 |
0 |
0 |
3,2 |
|
10:00 |
3,2 |
0 |
0 |
0 |
3,3 |
|
10:15 |
3,3 |
0 |
0 |
0 |
3,3 |
|
10:30 |
3,3 |
0 |
0 |
0 |
3,2 |
|
10:45 |
3,2 |
0 |
0 |
0 |
3,0 |
|
11:00 |
3,0 |
12 |
0 |
0 |
0,0 |
Набор входных данных для искусственной нейронной сети включает:
? уровень глюкозы в крови (ммоль/л) – столбец «Уровень гликемии», в котором указаны измерения гликемии пациента через каждые 15 минут;
? приёмы пищи – столбец «Приём пищи», в котором указано количество потребляемых углеводов в граммах за основные приёмы пищи пациента (завтрак в 8:00, второй завтрак в 11:00, обед в 13:00, полдник в 16:00, ужин в 18:00, второй ужин в 20:00 и перекус перед сном в 22:00);
? инъекция короткого инсулина Humulin S (единицы) – столбец «Короткий», в котором указана доза инсулина перед едой, введенная за 15 минут до еды (перед завтраком в 7:45, перед обедом в 12:45 и перед ужином в 17:45 соответственно);
? инъекция длинного инсулина Humulin L (единицы) – столбец «Базальный», в котором указана доза инсулина, введенная пациентом утром в 7:45 и вечером перед сном в 22:00.
Выходные данные:
На выходе нейронной сети необходимо получить прогноз гликемии – предсказанные значения гликемии, измеренные через 15 минут после данного значения уровня гликемии.
Столбец «Прогноз» содержит целевые значения гликемии, измеренные через 15 минут после данного значения уровня гликемии. Данный столбец используется при обучении нейронной сети.
Архитектура искусственной
нейронной сети
Для прогнозирования уровня гликемии была разработана искусственная нейронная сеть на основе рекуррентной искусственной нейронной сети Элмана (см. рис. 1).
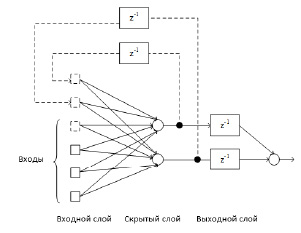
Рис. 1. Искусственная нейронная сеть на основе рекуррентной сети Элмана
В составе сети находятся 3 слоя: входной, скрытый и выходной. Нейронная сеть Элмана образуется из многослойного персептрона [7] введением обратных связей, выходящих из нейронов скрытого слоя. Это позволяет учесть предысторию наблюдаемых процессов и накопить информацию для более точного прогнозирования.
Входными узлами в разработанной искусственной нейронной сети являются 4 входных атрибута: уровень глюкозы в крови, количество углеводов в граммах, инъекция короткого инсулина Humulin S и инъекция длинного инсулина Humulin L. В скрытом слое сети находятся 2 нейрона. Их задачей является получение входных данных от входных узлов и передача выходных данных выходным узлам (z-1). Скрытый слой имеет сигмоидальную передаточную функцию гиперболического тангенса. На выходе сети находится 1 нейрон. Выходной нейрон имеет линейную функцию активации.
Методом обучения многослойной искусственной нейронной сети является алгоритм Левенберга – Марквардта, который определен в следующем уравнении:
xk+1 = xk – [H – μI]g,
где xk – это значение функции минимизации ошибки на текущей эпохе обучения, а xk+1 – это значение функции минимизации ошибки на следующей эпохе обучения, H – это матрица Гессе, μ – скаляр, I – единичная матрица, а g – градиент. Данный алгоритм второго порядка сходится намного быстрее в отличие от стандартного алгоритма обратного распространения ошибки, исторически используемого в нейронной сети Элмана. В связи с этим становится очевидно, что для достижения минимума целевой функции требуется меньшее количество эпох обучения.
Инициализация весов была выполнена с помощью функции инициализации Нгуен – Видроу (название в MATLAB – «initnw»). Ввиду того, что значения случайны, обучение любых двух сетей начинается с уникального набора весов нейронов. Поэтому результаты работы каждой обученной нейронной сети не обязательно будут повторяться.
Разбиение данных в модели происходило в следующем процентном соотношении: обучающая выборка составляла 60 % от объема исходных данных, на выборку валидации приходилось 20 % и на тестовую выборку 20 % соответственно [8].
Критерий успеха обучения оценивался значением среднеквадратичной ошибки, которая определяется как корень из квадрата разности целевого и предсказанного значений.
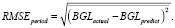
Показатели ошибки измеряют предсказательную эффективность модели регрессии с точки зрения среднего отклонения ее прогнозов от истинных, поданных на вход модели значений. Чем ниже значения ошибок, тем точнее прогноз модели. Если общий показатель ошибок равен 0, значит, модель идеально подбирает данные.
Анализ результатов прогнозирования
В среднем для обучения модели было необходимо 24–30 эпох. В результате среднее квадратичное отклонение составило 0,05 ммоль/л, градиент – 0,25, параметр μ равен 10-5. Результаты 15-минутного предсказания уровня глюкозы в крови представлены на рис. 2. На данном графике одна временная единица равна 15-минутному интервалу между измерениями. Как видно на графике, предсказанные значения находятся довольно близко к реальным значениям, что позволяет утверждать об успешности предсказания и адекватности полученной модели.
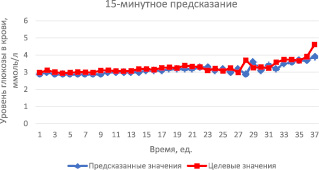
Рис. 2. Результаты 15-минутного предсказания уровня глюкозы в крови за 9,5 часов
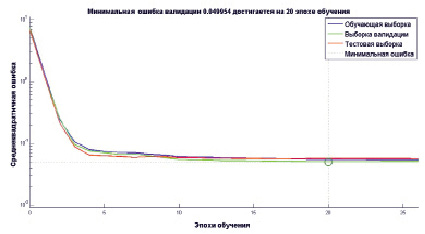
Рис. 3. Среднеквадратичная ошибка в зависимости от эпохи обучения
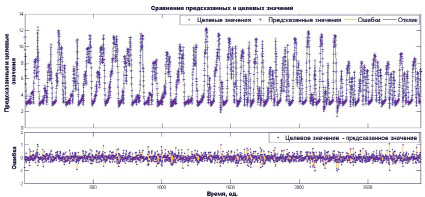
Рис. 4. Сравнение реальных и предсказанных значений
На рис. 3 показано изменение средней квадратичной ошибки в процессе обучения модели.
На рис. 4 отображено значение абсолютной ошибки для каждого элемента из исходного множества данных. Одна временная единица равна 15-минутному интервалу между измерениями. Максимальное отклонение прогнозируемого значения от реального составляет не более 1,5 ммоль/л.
Успешность полученных результатов открывает возможность для построения более длительных предсказаний. В сочетании с конфигурацией сети данного исследования может использоваться рекуррентная нейронная сеть [9] в режиме реального времени. Это позволит сравнить точности прогнозирования сетей в течение длительного периода времени. Использование данных реальных пациентов, которые будут собраны с устройств длительного мониторинга глюкозы в крови с частотой дискретизации, аналогичной частоте дискретизации AIDA, позволит исследовать влияние шума гликемического детектора, а также факторов стресса, физических нагрузок и болезней на точность прогнозирования.
Заключение
Спроектированная искусственная нейронная сеть на основе рекуррентной сети Элмана с использованием алгоритма Левенберга – Марквардта смогла построить краткосрочное предсказание уровня глюкозы в крови со средней квадратичной ошибкой 0,05 ммоль/л. Дальнейшие области исследования будут посвящены построению долгосрочных предсказаний на основе разработанной модели, а также разработке альтернативных нейросетевых парадигм, способных к длительному обучению. Применение длительного мониторинга глюкозы в крови [10], а также устройств для введения инсулина позволит существенно расширить набор входных данных о пациентах в парадигмах искусственных нейронных сетей. Использование данных нескольких пациентов также необходимо для доказательства достоверности предсказательной точности искусственной нейронной сети. Это позволит анализировать изменчивость индивидуальных значений.
Библиографическая ссылка
Биленко А.А., Биленко А.Ф., Белов Ю.С. ПРОГНОЗИРОВАНИЕ УРОВНЯ ГЛЮКОЗЫ У ПАЦИЕНТОВ С САХАРНЫМ ДИАБЕТОМ 1 ТИПА НА ОСНОВЕ НЕЙРОСЕТЕВОЙ ПАРАДИГМЫ // Современные наукоемкие технологии. 2018. № 2. С. 21-26;URL: https://top-technologies.ru/ru/article/view?id=36900 (дата обращения: 16.02.2026).



