Каждому педагогу в настоящее время приходится сталкиваться с трудностями, обусловленными таким явлением, как глобализация. Это процесс всемирной экономической, политической и культурной интеграции и унификации. Его следствием является изменение методики образовательного процесса, как в школе, так и в высших учебных заведениях. Глобализация образования приводит к приспособлению системы обучения к запросам глобальной рыночной экономики. Образовательный процесс должен меняться, подстраиваться под реалии нашего времени.
В высших учебных заведениях дисциплина «Математика» изучается по одинаковой программе с отличием только в количестве учебных часов без учёта будущей профессии студента. Однако именно от выбранного направления или специальности должно зависеть содержание курса математики, подбор заданий с применением изучаемых математических понятий [1, с. 59].
Существует необходимость в такой организации процесса обучения математике, который будет учитывать особенности обучающихся, при этом образовательный процесс должен быть поставлен в соответствие с дидактическими принципами: системности, доступности, межпредметности обучения, мотивационного обеспечения учебной деятельности [2, с. 65].
Принцип системности обучения. Должно осуществляться последовательное и систематическое наполнение курса математики материалом прикладного характера, связанным с будущей профессией обучающихся. Это может быть реализовано при использовании тестовых технологий, в которых каждый раздел дисциплины может быть обеспечен задачами разного уровня сложности [2, с. 66].
Принцип доступности обучения. Материал других дисциплин, используемый в образовательном процессе обучения математике для иллюстрации математических понятий или в решении прикладных, профессионально ориентированных задач, должен быть доступен студентам. Возникает необходимость снабжения обучающихся справочным материалом и методическими рекомендациями.
Принцип межпредметности обучения. Дисциплина «Математика» должна быть взаимосвязана с другими дисциплинами, изучаемыми студентами далее в учебном процессе. Планируемым результатом освоения образовательной программы является формирование у студентов набора определённых компетенций.
Крайне важным показателем уровня освоенности предмета являются остаточные знания. Главной целью занятий следует поставить не «прохождение» темы, а «понимание» её, так как многие понятия и правила со временем забываются, это естественный процесс, однако грамотный образованный специалист должен владеть ключевыми понятиями, методами и приёмами применения знаний на практике. Важной частью как практического, так и лекционного занятия следует сделать вспоминание основных понятий и формул уже изученного материала. Достаточно посвятить в начале каждого занятия несколько минут вопросам типа: «что такое…», «где используется…», «как определить…». Это позволит обучающимся постоянно освежать в памяти знания пройдённой темы и тем самым прочно запоминать материал. Данный вариант обучения позволит студентам освоить основной материал, уверенно решать основные задачи и овладеть математической культурой, достаточной для решения большинства профессиональных задач.
Достигнуть полного понимания предмета можно только при условии формирования у студента заинтересованности к обучению, то есть его мотивации.
Цель исследования
Образовательная деятельность обучающегося эффективна при условии, что в её основе лежит необходимость в приобретении математических знаний и умений для дальнейшей учёбы и работы. В связи с этим необходимо использовать профилированное обучение математике с применением материала общепрофессиональных дисциплин. Анализ подобных заданий вызывает у студентов больший интерес и внимание по сравнению с отвлечёнными задачами из учебников, содержащих обычно материал, не связанный с профессией.
Поэтому появляется необходимость в дифференцированном подходе к изучению дисциплины «Математика» студентами различных специальностей. Обучение математике в вузе ведётся с целью интеграции знаний, навыков и умений студентов, развития математических способностей и применения их в будущей профессии. Направления математики, не используемые при изучении специальных дисциплин, могут быть рассмотрены обзорно либо даваться на самостоятельное изучение. Разделы же математики, на которых базируются профильные дисциплины, необходимо изучать более подробно. Предложенная организация учебного процесса позволяет эффективно использовать постоянно уменьшающееся время аудиторных занятий и наиболее полно учитывать способности и интересы студентов. Широкие возможности использования математических понятий, теорий и методов в разнообразных областях знаний дают возможность утверждать, что если обучение математике имеет профессиональное направление, то это приводит к формированию положительной мотивации у студентов к изучению данной дисциплины. Обобщённой целью исследования является разработка примеров прикладных задач линейной алгебры с элементами аналитической геометрии для студентов специальности 38.05.02 «Таможенное дело».
Материалы и методы исследования
Рассмотрим вариант использования профессионально-ориентированного обучения курса математики на примере изучения студентами специальности «Таможенное дело» раздела «Линейная алгебра с элементами аналитической геометрии». Дисциплина «Математика» является обязательной во всех высших учебных заведениях, поскольку развитие гуманитарных наук без использования основных понятий и методов математического моделирования, а также количественных методов исследования, широкого применения современных вычислительных средств невозможно. Таким образом, важнейшей, а следовательно, и обязательной составляющей фундаментальной подготовки специалиста является математическое образование [3].
Выпускники таможенного дела должны владеть знаниями, находящимися на стыке следующих направлений – экономики и юриспруденции. Особенность характеризуемой специальности выставляет новые требования для дисциплины «Математика». Управление процессами, протекающими в области таможенного дела, выяснение ведущих тенденций их развития, селекция юридической и экономической информации, правильная оценка получаемых статистических данных – неполный перечень проблем, возникающих на стыке математики и таможенного дела.
Результаты исследования и их обсуждение
Раздел «Линейная алгебра с элементами аналитической геометрии» посвящён изучению матриц и действий с ними, расчёту определителей, нахождению обратной матрицы, собственным числам и собственным векторам матрицы, системам линейных уравнений.
Обычно на первом лекционном занятии при изучении данной темы вводятся понятия матрицы, определителя, их свойств и действий с ними. Такой подход к обучению студентов-таможенников даёт отрицательный результат в связи с тем, что для гуманитариев достаточно сложно усваивать долгие математические выкладки. Поэтому, чтобы заинтересовать обучающихся материалом, можно после введения основных понятий и определений отметить их многочисленные способы применения и в специальных дисциплинах, в числе которых область таможенного дела. Это становится возможным, поскольку значительная часть математических моделей объектов в экономике, а также различные процессы в этой области можно записать в удобной и, главное компактной матричной форме.
Действия с матрицами могут быть рассмотрены в практических примерах следующего плана.
Пример прикладной задачи 1. Рассчитайте размер таможенной пошлины (в валюте РФ) на ввозимый на территорию РФ товар. Партия товара представляет собой продукцию трёх видов: А, В, С. Известно, что таможенная стоимость продукции вида А равна 3500 рублей, для вида В стоимость составляет 4500 рублей, для С – 2000 рублей. Ставка пошлины для каждого вида продукции соответственно равна 25, 30 и 20 % [4].
Представим партию товара, состоящую из трёх видов матрицей X = (3500 4500 2000), а ставки пошлины для каждого из товаров – матрицей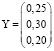 
. Тогда искомый размер таможенной пошлины на весь товар Z = X•Y = (3500 4500 2000)×
.
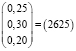Ответ: 2625 рублей.
Пример прикладной задачи 2. На предприятии изготавливают продукцию четырёх видов: P1, P2, P3, P4, при этом используют сырьё трёх типов: S1, S2, и S3. Нормам расхода сырья соответствует матрица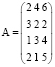 
, где каждый элемент aij = (i = 1, 2, 3, 4; j = 1, 2, 3) показывает, сколько единиц сырья j-го типа расходуется на производство единицы продукции i-го вида. План выпуска продукции представлен матрицей C = (200 130 90 110), а стоимость единицы каждого типа сырья (ден. ед.) – матрицей 
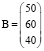. Определите общую стоимость сырья [5].
Матрица стоимости затрат сырья на единицу продукции вычисляется по формуле
R =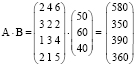 
,
тогда общая стоимость сырья составляет
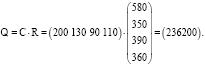
Ответ: 236200 ден. ед.
Для изучения данного раздела математики можно ввести модель Леонтьева многоотраслевой экономики (балансовый анализ), так как межотраслевой баланс содержит важные для специалиста таможенного дела данные о распределении продукции по элементам конечного потребления (товарооборот, производственные и непроизводственные капитальные вложения, экспорт, импорт и т.д.), о национальном доходе. В модели Леонтьева наглядно представлено практическое использование обратных матриц.
Пример задачи на балансовый анализ. Вектор непроизводственного потребления задан матрицей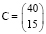 
, а матрица межотраслевого баланса имеет вид 
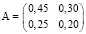. Найти вектор валового выпуска, обеспечивающий данный вектор потребления [6, с. 37].
Вектор валового выпуска находится по формуле
X = (E – A)-1•C,
где Е – единичная матрица.
Обратную матрицу (E – A)-1 находим с помощью использования миноров.
,
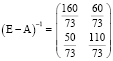тогда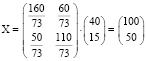 
.
Ответ: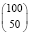 
.
Знания о собственных числах и собственных векторах матриц, а также о решении систем линейных уравнений необходимы при рассмотрении линейной модели обмена (модуля международной торговли).
Пример задачи на линейную модель обмена. Дана структурная матрица торговли трёх стран S1, S2, S3: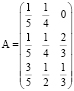 
. Определить соотношение национальных доходов стран для сбалансированной торговли.
Найдём собственный вектор Х матрицы А, отвечающий собственному значению l = 1. Координаты собственного вектора находятся из матричного уравнения (A – E)•X = или однородной системы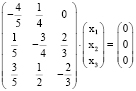 
. Решаем её методом Гаусса и получаем координаты собственного вектора 
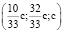. Полученный результат показывает, что сбалансированность торговли трёх стран достигается при соотношении национальных доходов стран 
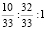или 10:32:33.
Ответ: 10:32:33.
Составление и решение систем линейных уравнений могут быть рассмотрены в следующем примере.
Пример задачи на составление систем линейных уравнений. В городе имеется три крупных завода, на которых работают 100000 рабочих. Других заводов в городе нет. Имеются данные о текучести кадров: за год из каждой тысячи работающих с завода А 20 человек переходят на завод В и 15 человек на завод С и т.д. (рисунок). Установить численность рабочих на каждом заводе при условии, что город живёт стабильной жизнью [7].
Фраза «город живёт стабильной жизнью» означает следующее: сколько с каждого завода увольняется рабочих, столько же принимается на него. Численность рабочих на заводе А обозначим через х, на заводе В – через y, на заводе С – через z. Получаем систему уравнений:
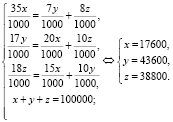
Ответ: численность рабочих первого завода составляет 17600 человек, второго – 43600 человек, третьего – 38800 человек.
Выводы
Предложенный вариант изучения конкретной темы позволит студентам специальности «Таможенное дело»:
– заинтересоваться предметом, так как включение в содержание образования профессионально значимых задач по изучаемой теме служит эффективным средством формирования положительной мотивации;
– понять, насколько математика необходима им в профессиональной деятельности, поскольку приведение конкретного примера позволяет максимально приблизить математику к реальной жизненной ситуации;
– связать материалы нескольких дисциплин.
Предлагаемая методическая система обучения математике способствует достижению общих целей (общекультурных, образовательных, прикладных и воспитательных) подготовки грамотных специалистов. Повышение интереса к предмету способствует развитию обучающихся средствами математики и повышает качество обучения, что обязательно скажется на итоговых результатах и оценках.
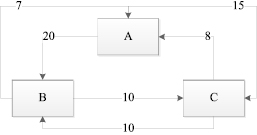
Условие к задаче на составление систем линейных уравнений
Разработанные примеры практических задач нашли применение в образовательном процессе специалистов таможенного дела как очной, так и заочной формы обучения. Указанная методика преподавания апробирована на 230 студентах первого и второго курсов специальности 38.05.02 «Таможенное дело».
Библиографическая ссылка
Бредихина О.А., Шеставина С.В., Головин А.А. ПРОФЕССИОНАЛЬНО-ОРИЕНТИРОВАННОЕ ОБУЧЕНИЕ ЛИНЕЙНОЙ АЛГЕБРЕ С ЭЛЕМЕНТАМИ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ СТУДЕНТОВ ТАМОЖЕННОГО ДЕЛА // Современные наукоемкие технологии. – 2018. – № 1. – С. 66-70;URL: https://top-technologies.ru/ru/article/view?id=36894 (дата обращения: 21.11.2024).