Решение задач проектирования систем управления динамическими объектами предполагает использование математических моделей исследуемого процесса в регуляторах. Априорные математические модели, полученные на основе физических законов, не всегда точно отражают исследуемые процессы. Для определения параметров математической модели используются алгоритмы идентификации, которые отличаются большим разнообразием и отличаются точностными характеристиками и необходимыми для реализации вычислительными затратами. С помощью исследуемых алгоритмов идентификации определяют неизвестные параметры матрицы модели, структура которой задана априори.
Точность идентификации параметров модели зависит от связей определяемого параметра в матрице модели с непосредственно измеряемой компонентой вектора состояния, а также от точности алгоритма идентификации. Точностные характеристики алгоритмов идентификации известны [1, 2]. Сильные связи идентифицируемого параметра с вектором измерения позволяют эффективно определить неизвестный параметр. Для определения интенсивности этих связей используются критерии степени параметрической идентифицируемости [3].
В настоящей статье представлены численные критерии степени параметрической идентифицируемости, разработанные для стационарных и нестационарных моделей, а также для одного класса нелинейных моделей динамических систем. Эффективность применения критериев продемонстрирована на примере идентификации неизвестного параметра моделей погрешностей инерциальной навигационной системы (ИНС) летательных аппаратов (ЛА).
В практических приложениях некоторые параметры матриц погрешностей ИНС зависят от режима полета и достоверно неизвестны, поэтому проводится их идентификация. Определение качества идентификации параметров модели позволяет осуществить выбор наиболее точных моделей, заранее оценить степень доверия результатам идентификации.
Постановка задачи исследования
В качестве алгоритмов построения моделей применяются эволюционные алгоритмы: нейронные сети, методы самоорганизации и генетические алгоритмы [4–6]. Эволюционные алгоритмы позволяют построить нефизичные модели, структура которых заранее неизвестна. Поэтому для управления используются физические модели с априорно известной структурой. При этом в процессе функционирования динамических объектов в условиях изменяющихся внешних воздействий параметры моделей могут существенно изменяться. И здесь возникает необходимость создания модели с использованием алгоритмов идентификации. Точностные характеристики алгоритмов идентификации известны [7]. Исследование качественных характеристик идентификации параметров проводится путем анализа результатов серий экспериментов и требует обработки большого объема статистического материала.
Наиболее эффективным подходом при решении задачи определения качества идентификации является использование критериев степени идентифицируемости [1–3]. С помощью методов определения степени идентифицируемости можно вычислить численные оценки качества идентификации конкретного параметра матрицы модели. На основе этой информации осуществляется выбор моделей исследуемых процессов, обладающих наилучшей идентифицируемостью.
Алгоритм идентификации
Математическая модель исследуемого динамического объекта имеет следующий вид [8]:
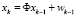, (1)
где xk-1 – вектор состояния; wk-1 – вектор входного шума, который является дискретным аналогом белого гауссового шума с нулевым математическим ожиданием; Ф – матрица модели с размерностью (n×m).
Часть вектора состояния измеряется:
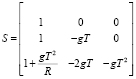, (2)
где zk – m-вектор измерений; Н – матрица измерений(m×n); vk – m-вектор измерительного шума, который является дискретным аналогом белого гауссового шума с нулевым математическим ожиданием, причем v и w некоррелированы между собой, т.е. М[vjwkT] = 0.
Необходимо произвести оценивание неизвестных постоянных параметров матрицы объекта Ф уравнения (1).
Оценка вектора состояния х1 при скалярном измерении z может быть определена следующим образом:
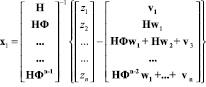. (3)
Уравнение измерений для (n + 1)-го момента времени имеет вид
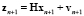. (4)
Вектор состояния xn+1 можно выразить через его значение в 1-й момент времени следующим образом:
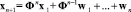. (5)
Подставив (5) в (4), получим
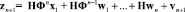(6)
или
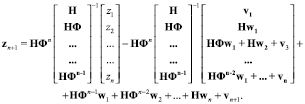(7)
Введем обозначения:
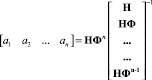; (8)
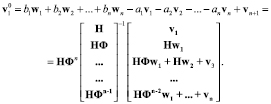(9)
Тогда уравнение (7) с учетом новых обозначений примет вид
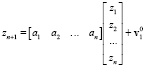. (10)
Уравнение (10) можно переписать в следующем виде:
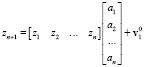, (11)
а также:
;
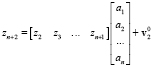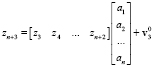; (12)
........................................
.
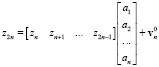Уравнения (12) можно записать в матричной форме:
,
откуда можно выразить вектор-столбец, состоящий из неизвестных параметров a1,a2,…,an:
.
В скалярной форме уравнение для вектора неизвестных параметров будет иметь вид
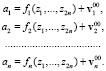(13)
Здесь
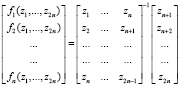; (14)
. (15)
Численный критерий степени идентифицируемости параметров нелинейных моделей одного класса
Предложенный критерий степени идентифицируемости имеет следующий вид
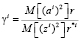. (16)
Здесь М[(ai)2] – дисперсия произвольной i-ой компоненты вектора параметров a;
М[(zi)2] – дисперсия непосредственно измеряемой компоненты вектора параметров;
r = M[v2] – дисперсия исходного измерительного шума;
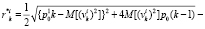
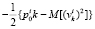– дисперсия приведенного измерительного шума;
p – дисперсия ошибки оценивания адаптивного фильтра;
v – обновляемая последовательность.
Разработанный численный критерий степени идентифицируемости конкретных параметров матрицы модели отличается универсальностью и позволяет вычислять качество идентификации параметров в виде скаляра.
В случае, когда уравнения объекта имеют явно выраженный нелинейный характер, используется критерий определения степени параметрической идентифицируемости нелинейных моделей динамических систем.
Пусть в уравнении объекта в SDC-представление вектор состояния xk+n можно выразить его значением в начальный момент xk времени в виде
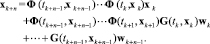(17)
Подставив выражение для xk+n в уравнение измерений yk+n, получим
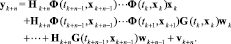(18)
Подставив в это уравнение выражение xk, получим
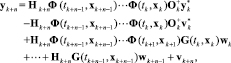(19)
где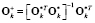 
– псевдообратная матрица 
.
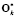Введем обозначения:
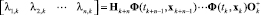, (20)
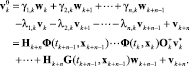(21)
Тогда задача сводится к определению неизвестных нестационарных элементов вектора-столбца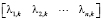 
по вновь сформированным измерениям [9]:
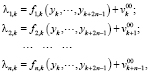(22)
где
;
.
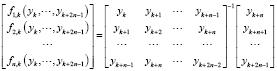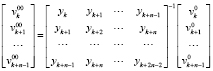Отсюда критерий степени идентифицируемости параметров модели динамических нестационарных систем имеет вид
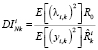, (23)
где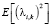 
- дисперсия произвольной i-ой компоненты вектора параметров λ; 
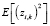– дисперсия непосредственно измеряемого вектора состояния; R0 – дисперсия исходного измерительного шума; 
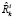? дисперсия приведенного измерительного шума.
Таким образом, уравнение (23) используется для определения степени идентифицируемости параметров матрицы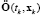 
.
Результаты исследования и их обсуждение
Проведено моделирование линейных математических моделей погрешностей ИНС [10–12] корректируемой от ГЛОНАСС с использованием алгоритмов идентификации. Для идентификации неизвестных параметров матрицы модели использован типовой алгоритм идентификации, в основе которого лежит скалярный алгоритм. На графиках представлены сглаженные результаты идентификации.
Линейная математическая модель погрешностей ИНС для одного горизонтального канала имеет вид
xk = Фxk-1 + Wk-1,
где
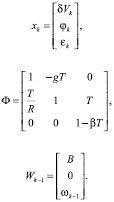
Здесь g – гравитационное ускорение; В – смещение нуля акселерометра, R – радиус Земли, Т – период дискретизации; w – средняя частота случайного изменения дрейфа, Wk-1 – дискретный аналог белого гауссового шума; δVk – ошибки ИНС в определении скорости, φk – углы отклонения ГСП от сопровождающего трехгранника, εk – скорость дрейфа ГСП.
На рис. 1 представлено гравитационное ускорение g, изменяющееся с увеличением высоты полета ЛА и результаты его идентификации.
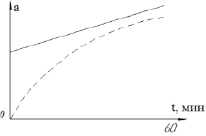
Рис. 1. Моделирование гравитационного ускорения g
На рис. 2 представлены погрешности ИНС и их оценки фильтром Калмана, полученные с использованием классической модели ошибок ИНС и с моделью с повышенными характеристиками идентифицируемости параметра.
Из графиков рис. 2 видно, что точность коррекции с использованием классической модели ошибок ИНС ниже, чем при использовании идентификации параметра матрицы модели g и выбора матрицы оцениваемого процесса с увеличенной степенью идентифицируемости этого параметра.
Таким образом, использование критерия степени идентифицируемости позволяет выделить параметры матрицы модели, поддающиеся эффективной идентификации, и за счет их использования повысить точность оценивания переменных состояния линейных систем.
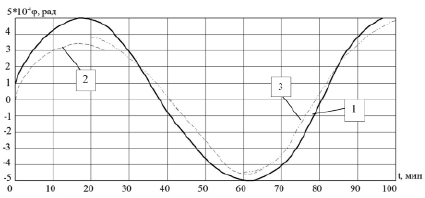
Рис. 2. Погрешности ИНС: 1 – ошибки ИНС, 2 – оценки фильтра Калмана с классической моделью, 3 – оценки фильтра Калмана с идентификацией параметра g
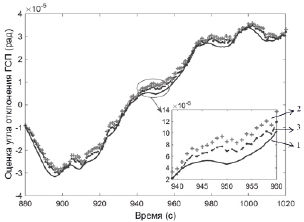
Рис. 3. Результаты моделирования нелинейных погрешностей ИНС: 1 – погрешности ИНС, 2 – оценки погрешности ИНС, полученные с помощью классического нелинейного фильтра Калмана; 3 – оценки погрешности ИНС, полученные с помощью нелинейного фильтра Калмана с повышенными характеристиками идентифицируемости
На рис. 3 представлены результаты моделирования нелинейных погрешностей ИНС, алгоритма оценивания классического нелинейного фильтра Калмана и нелинейного фильтра Калмана с улучшенной моделью.
Результаты математического моделирования продемонстрировали работоспособность и достаточно высокую точность алгоритмов, использующих математические модели с высокими степенями идентифицируемости неизвестных параметров.
Заключение
Рассмотрены численные критерии степени идентифицируемости параметров матрицы стационарной, нестационарной и нелинейной моделей. Представлены результаты математического моделирования тестовой модели погрешностей ИНС с алгоритмами фильтра Калмана, которые подтверждают эффективность использования для оценивания моделей с повышенными характеристиками идентифицируемости.
Библиографическая ссылка
Цибизова Т.Ю., Пьо Си Тху, Селезнева М.С. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ДИНАМИЧЕСКИХ СИСТЕМ С ИСПОЛЬЗОВАНИЕМ ПАРАМЕТРИЧЕСКОЙ ИДЕНТИФИЦИРУЕМОСТИ // Современные наукоемкие технологии. – 2018. – № 1. – С. 54-60;URL: https://top-technologies.ru/ru/article/view?id=36892 (дата обращения: 21.11.2024).