Современные высокоточные бесплатформенные инерциальные навигационные системы (БИНС) строятся на базе оптических гироскопов, в частности кольцевых лазерных и волоконно-оптических гироскопов [1]. Относительно недавно появился новый тип оптических гироскопов, объединивший основные достоинства известных двух систем и получивших название – кольцевой моноблочный гироскоп с полупроводниковым лазерным диодом (КМГ с ПЛД) [2]. Устройство обладает возможностью масштабирования периметра оптического контура на базе моноблока и использует в качестве источника накачки микромощный полупроводниковый лазер. Новая конструкция лазерного гироскопа позволяет использовать открытые оптические каналы и допускает применение более дешевых конструкционных материалов, например органического стекла, оптического полистирола и т.п. Это существенно упрощает технологию создания оптического моноблока и позволяет применить большее количество стандартных изделий – линейки полупроводниковых лазерных диодов, элементов обвязки оптического контура моноблока на базе стандартных зеркал, интерференционного смесителя. Однако для моноблока, изготовленного из органического стекла (полиметилметакрилат), коэффициент линейного теплового расширения варьируется в широких пределах и равен 60–110x10-6 1/0К. Это приводит к искажению линейности и соосности оптических каналов при рабочих температурах изделия в диапазоне 20–75 °С, что изменяет цилиндрическую геометрию канала.
Объектом исследования является кольцевой моноблочный гироскоп с полупроводниковым лазерным диодом, в котором стабилизация рабочего режима излучения микромощного ПЛД выполняется на базе элемента Пельтье [3]. При выходной мощности лазера 100 мВт и более металлический корпус, выполняющий функции радиатора, разогревается до температур десятков градусов Цельсия, что создает при его контакте с конструкционным материалом моноблока температурное дестабилизирующее воздействие на оптический контур гироскопа в виде теплового изгиба и деформации составляющих оптических каналов. Кроме того, окружающая среда на борту летательного аппарата также оказывает негативное влияние на тепловой режим моноблока гироскопа.
Цель работы – повысить температурную стабильность кольцевого моноблочного гироскопа с полупроводниковым лазерным диодом.
Задачей исследования является разработка способа компенсации температурного градиента вдоль оптических каналов, составляющих контур гироскопа, и математической модели температурной зависимости оптического канала лазерного гироскопа.
Описание объекта исследования. Объектом исследования является КМГ с ПЛД (рис. 1, а), изготовленный из органического стекла (рис. 1, б) [2]. Макетный образец создан на ОАО НПК «ЭЛАРА». Устройство содержит многоугольный оптический моноблок 1 со сформированными в нем оптическими каналами 2, зеркала полного отражения лучистой энергии 3 и интерференционный преобразователь 4, совмещенный с полупрозрачным сферическим зеркалом. Сферическое зеркало обеспечивает юстировку треугольного оптического контура в моноблоке за счет применения механической двухкоординатной системы. При диаметре оптического канала 2,5 мм минимальная толщина моноблока составляет 8–10 мм, а длина оптического канала масштабируема и рекомендуется 50, 100 или 150 мм. В качестве оптического термостабильного источника накачки гироскопа используется микромощный ПЛД 6 марки LFO-250, снабженный элементом Пельтье, который расположен в геометрическом центре моноблока. Выходная мощность излучения лазерного диода 250 мВт, длина волны генерации 1,5 мкм, потребляемый ток элемента Пельтье 5,0 А. Двунаправленное излучение и реализация одномодового режима достигается сопряжением ПЛД 6 с внешним оптическим резонатором 5 типа «усеченная призма». Последнее условие позволяет реализовать режим эффекта Саньяка в гироскопе [1].
Способ компенсации температурного градиента в оптическом канале. При симметричной геометрии моноблока и однородности конструкционного материала можно считать, что температурное поле линейно изменяется во всех направлениях от центра треугольника. Учитывая, что рабочий режим КМГ с ПЛД реализуется при фиксированной мощности ПЛД, то температура корпуса источника возмущения априори известна и ее влияние можно компенсировать с учетом температуры внешней окружающей среды.
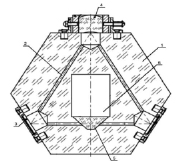
а) б)
Рис. 1. Лазерный гироскоп
Различие геометрического места точек оптического канала относительно источника дестабилизирующей температуры определяет градиент температуры вдоль его длины. Это приводит к искривлению линейной геометрии оптического канала, его формы, искажению оптического потока в контуре и нарушению режима работы гироскопа.
Введем понятие критической точки/зоны оптического канала, в которой разбаланс температуры между центром оптического канала и ее линейной длины превышает некоторый порог, приводящий к изгибу и деформации канала. Установлено, что при длинах оптических каналов 100 мм и более при рабочих значениях температур корпуса ПЛД и окружающей среды критические точки находятся по краям оптических каналов.
Разработанный способ состоит в том, что от источника теплового возмущения формируются не менее двух на каждый оптический канал специальные компенсирующие каналы с повышенным коэффициентом теплопроводности и вектором, направленным в критическую точку/зону оптического канала [4]. За время выхода КМГ с ПЛД на установившийся рабочий режим градиент температур в критических точках/зонах купируется. Практически разбаланс по температуре в критических точках не должен превышать 5–10 %, что для канала диаметром 2,5 мм при длине 100 мм определяет диапазон деформации 0,125–0,25 мм. Технически задача решается применением, например, теплопроводных паст типа КПТ-8 или их аналогов [5].
Фактически возмущающий тепловой поток, направленный к середине оптического канала по материалу моноблока, компенсируется тепловым потоком по сформированному каналу компенсации заданной формы и геометрии в критическую точку/зону на краях этого оптического канала, чем достигается компенсация температурного градиента вдоль него.
Математическая модель температурной зависимости оптического канала. Модель влияния температурного поля источника возмущения представлена на рис. 2, а. Источник тепла Т рассматривается как точечный с диаметром 2r и моделирует работу элемента Пельтье в микромощном ПЛД. В критических точках К выполняется условие Т2 < Т1. Концентрические окружности отражают распределение поля температуры от источника возмущения Т в однородном пространстве исследуемого моноблока [6]. Конструктивно источник температурного возмущения Т размещен внутри оптического контура моноблока (R>>r), выполненного из оптически прозрачного материала, например органического стекла. Выделенные каналы компенсации (обозначены зеленым цветом) направлены в критические точки К.
Структурная схема компенсации температурного градиента оптического канала моноблока в критических точках (рис. 2, б) содержит два динамических звена постоянного запаздывания, которые моделируют прохождение информационного сигнала (температуру источника нагрева моноблока Т(Р, τ) и окружающей среды Тср) по моноблоку и по каналу компенсации. Сумматор на входе определяет одновременное влияние двух информационных сигналов, а сумматор на выходе – реализует сравнение температур вдоль оптического канала между центром оптического канала Т1(τ) и критической точкой Т2(τ).
Здесь Кн – коэффициент линейного теплового расширения конструкционного материала моноблока; Кк – коэффициент линейного теплового расширения конструкционного материала канала компенсации; α, β – коэффициенты теплопроводности материалов моноблока и канала компенсации; τ – текущее время; Р – мощность элемента Пельтье.
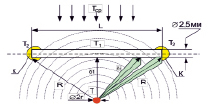а) 
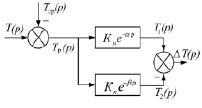б)
Рис. 2. Влияние температурного режима лазерного диода на геометрию оптического канала моноблока
Оператор системы компенсации определяется передаточной функцией Лапласа вида
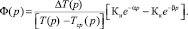(1)
Откуда выходной сигнал разбаланса в системе будет равен
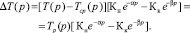
После обратного преобразования Лапласа режим компенсации во времени определяется следующим выражением:
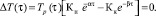(2)
В итоге, при заданном соотношении температур источника нагрева моноблока Т(τ) и окружающей среды Тср(τ), получим следующее соотношение:
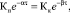(3)
определяющее возможность компенсации влияния дестабилизирующих температурных факторов на деформацию оптических каналов моноблока.
Необходимо рассчитать конструктивные параметры канала компенсации при заданных ограничениях на линейные геометрические размеры оптического канала L, температуру источника возмущения Т и значения теплопроводности материала моноблока.
Предположим, что температуры окружающей среды Тср и источника возмущения Т априори заданы и можно говорить о результирующей температуре Тр. Будем считать, что температура в объеме моноблока не зависит от времени, а зависит только от одной пространственной координаты, т.е. имеет место одномерный стационарный процесс теплопроводности [7]. Для одномерного стационарного процесса уравнение теплопроводности в цилиндрических координатах при отсутствии внутреннего тепловыделения имеет следующий вид [6]:
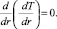(4)
Для i-ой точки (рис. 3, а) радиусом δi < R значение температуры Т(δi) при двух граничных условиях T(r) = T1 и T(R) = T2 можно найти из следующего выражения:
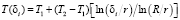. (5)
Поскольку закон распределения температуры априори известен, то тепловой поток вдоль сектора с радиусом δi при достаточно малом угле dφ можно определить с помощью закона Фурье для цилиндрической системы координат:
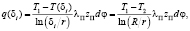(6)
где λП – коэффициент теплопроводности теплопроводной пасты; ZП – координата, определяющая толщину сектора канала с повышенной теплопроводностью.
Полный тепловой поток Q является интегральной величиной поперечной площади F:
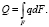(7)
Распределение поля температуры вдоль оптического канала длиной L до начала критической зоны в районе точки Т2 можно определить через величину δi при решении уравнения следующего вида:
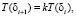(8)
где k – коэффициент пропорциональности, характеризующий критическую разность градиента температуры, приводящую к нарушению работы гироскопа.
Предположим, что имеет место влияние теплообмена между моноблоком и каналом компенсации, где коэффициенты теплопроводности между зонами различны. Примем реальное значение k равным 0,95. Тогда градиент распределения поля температуры вдоль оптического канала длиной L будет равен критической границе в 5 %. При k = 0,95 уравнение (8) с учетом (5) примет следующий вид:
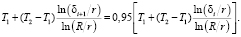(9)
Решение уравнения (9) будем искать в следующем классическом виде [6]:
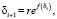(10)
где
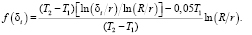
Рассмотрим частный случай: r = 5 мм; L = 100 мм; δi = δ1. Получим следующее выражение для промежуточной точки δ1,2 ≤ R, определяющей начало критической зоны Т2:
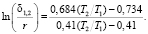(11)
Из уравнения (11) для δ1,2 ≤ R получим следующее соотношение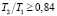 
, которое определяет значение критической границы в 16 %. Это превышает заданную величину границы в 5 % и определяет необходимость компенсации температуры возмущения.
Расчет параметров компенсирующего канала КМГ с ПЛД. При указанных ранее ограничениях для оптического канала L < 150 мм достаточно компенсировать две критические точки (рис. 3, а). Фактически необходимо рассчитать канал компенсации в точку 2, так как вторая является зеркальной относительно середины оптического канала.
Априори известно конструктивно-топологическое решение канала компенсации (рис. 3, б). В процессе синтеза определяются: коэффициент теплопроводности пасты λП при заданной толщине канала компенсации ZП, зона заполнения канала теплопроводной пастой с радиусом δ1,2. Оптимальное решение достигается при минимизации квадратичного функционала качества вида:
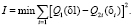(12)
Здесь мощности передающей тепловой энергии Q1 и Q2 источника температурного возмущения в точках 1 и 2 могут быть получены на основе общего выражения (7).
Выбранный профиль канала компенсации (рис. 4, б) для оптического канала L = 100 мм позволяет конкретизировать выражения Q1 и Q2 для критической точки 1.2:
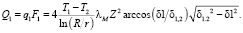(13)
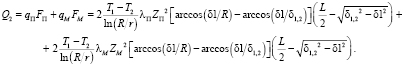(14)
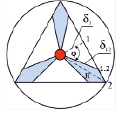
а)
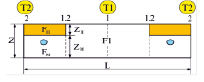
б)
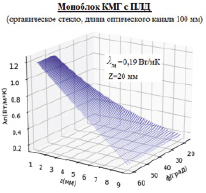
в)
Рис. 3. КМГ с ПЛД: вариант создания канала компенсации температурного возмущения в основании моноблока
Функционал качества достигает минимума при равенстве Q1 = Q2. Тогда
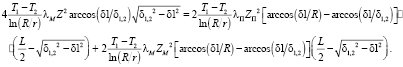(15)
Численное решение полученного уравнения (15) приведено на рис. 3, в, где представлены расчетные данные для выбора параметров канала компенсации. Для рассчитанного значения радиуса δ1,2 определен его угол φ, что позволяет выбрать геометрию канала, соответствующие значения теплопроводности пасты λП и его толщины ZП.
Выводы
Разработанная математическая модель температурной зависимости оптического канала КМГ с ПЛД, учитывающая влияние элемента Пельтье и температуру окружающей среды, позволила определить возможность компенсации возникающего температурного градиента вдоль оптического канала контура гироскопа.
Способ компенсации температурного градиента в оптическом канале КМГ с ПЛД базируется на том, что от источника теплового возмущения, расположенного в геометрическом центре моноблока, формируются не менее двух на каждый оптический канал специальные каналы компенсации с повышенным коэффициентом теплопроводности по отношению к коэффициенту теплопроводности материала моноблока и вектором, направленным в критическую точку/зону оптического канала. Понятие критической точки/зоны оптического канала определяется условием, при котором разбаланс температуры между центром оптического канала и ее линейной длины превышает порог в 5 %, приводящий к изгибу и деформации канала.
Для КМГ с ПЛД, изготовленного из органического стекла толщиной 20 мм при длине оптического канала 100 мм и реализующего треугольную оптическую схему гироскопа, рассчитаны конструктивные параметры канала компенсации, позволяющие исключить тепловой изгиб и деформацию оптических каналов моноблока лазерного гироскопа в заданных пределах.
Разработанная модель приемлема для расчета оптических контуров лазерного гироскопа с длинами оптических каналов более 150 мм, когда требуется четыре и более каналов компенсации на один оптический канал.
Библиографическая ссылка
Ус Н.А., Задорожний С.П. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ТЕМПЕРАТУРНОЙ ЗАВИСИМОСТИ ОПТИЧЕСКОГО КАНАЛА ЛАЗЕРНОГО ГИРОСКОПА // Современные наукоемкие технологии. – 2018. – № 1. – С. 48-53;URL: https://top-technologies.ru/ru/article/view?id=36891 (дата обращения: 21.11.2024).