Комплектация бортовой аппаратуры космического аппарата (КА) высоконадежными электронными компонентами (ЭКБ) является одной из наиболее важных задач, стоящих перед космической отраслью [1]. В первую очередь испытательно-технические центры преследуют цель предотвращения попадания в аппаратуру низкосортной контрафактной продукции, не удовлетворяющей требованиям надежности. Для этого необходимо обеспечить приобретение ЭКБ у авторизованных поставщиков, а также проведение в достаточном объеме входного контроля (ВК), дополнительных отбраковочных испытаний (ДОИ) и разрушающего физического анализа (РФА) поступающих партий изделий. Особое значение при этом уделяется индивидуальной отбраковке компонентов [2–4].
Необходимо отметить, что поставляемые партии ЭКБ могут быть неоднородными по своему составу, изготовленными из нескольких производственных партий кремниевых пластин [2]. Поэтому относить результаты входного контроля и дополнительных отбраковочных испытаний на выборке ЭКБ ко всей поставленной партии компонентов необходимо осторожно, как минимум с убеждением в том, что данная партия изготовлена из одной партии пластин (кристальных партий), или разброс параметров использованных пластин партий невелик. Это связано с тем, что относительно незначительные отклонения в производственном процессе могут повлиять на характеристики чувствительности, например, к воздействию радиационного излучения. Анализ приобретаемых партий ЭКБ на однородность становится особенно актуальным для ЭКБ с высоким уровнем интеграции, где флуктуации технологического процесса приводят к ошибкам в оценке качества, а величина ошибки непосредственно влияет на срок активной работы бортовой аппаратуры (БА).
Анализ особенностей использования электронных компонентов в космосе
Необходимо определить, из какого количества однородных по составу групп (кластеров) собрана производственная партия ЭКБ. Это особенно важно для импортных компонентов уровня качества «Industry», где не существует требований к однородности продукции, также для уровня качества «Military» без гарантии радиационной стойкости, а также для оценки «жизненного цикла» (steady state life test). Если поставленная совокупность компонентов состоит из нескольких различных групп, то для того, чтобы иметь обоснованное мнение о ее качестве, необходимо провести испытания для каждой группы, предварительно их выделив [4, 5]. Формирование выборок для оценки качества ЭКБ проводится по следующим критериям:
– ЭКБ изготовлены из одной кристальной партии пластин – одна выборка;
– ЭКБ изготовлены не из одной кристальной партии пластин – определение количества однородных групп, количество выборок равно количеству групп.
Формирование выборок должно производиться из ЭКБ, прошедших ДОИ и РФА, так как после этих процедур отсеиваются экземпляры, не удовлетворяющие требованиям к аппаратуре, и результаты оценки не искажаются изделиями с потенциальными дефектами. Кластеризация ЭКБ важна с точки зрения обеспечения надежности и, в еще большей степени, радиационной стойкости. Ионизирующие излучения как физический фактор космической среды во многом определяют срок активного существования космических аппаратов [6, 7].
Современные методы кластерного анализа предлагают широкий выбор средств выявления разнородных по совокупности параметров групп. Наиболее распространенным из подобных методов является метод к-средних (k-means) [8]. Алгоритмы, реализующие данный метод, являются алгоритмами глобальной оптимизации и зависят от выбора начальных значений (усредненных параметров центров групп – кластеров). В то же время метод выявления различных по параметрам групп изделий должен давать воспроизводимые результаты. Существенно повысить точность методов классификации позволяют алгоритмы, предложенные в [9, 10], которые могут стать основой автоматизированной системы по выявлению различных по параметрам групп изделий.
Специальные партии электронных компонентов
Основные характеристики качества и надежности определяются в процессе производства. В процессе комплектации КА приходится приобретать ЭКБ самого высокого уровня качества, который существует в России (ВП, ОС), и затем проводить серьезную работу по отбраковке потенциально ненадежных компонентов, чтобы оставшиеся образцы удовлетворяли требованиям к КА. Опыт работы с заводами-изготовителями показывает, что их серийная продукция не всегда удовлетворяет предъявляемым требованиям. В этой связи актуальной становится организация работы по выпуску специальных партий изделий для космической отрасли (так называемых «спецпартий»).
Для формирования списка дополнительных требований к спецпартиям проведен анализ состава и последовательности испытаний ЭКБ, проводимых по американским стандартам [2] для интегральных схем (ИС) и полупроводниковых приборов (ППП) [11] категории качества «Space» (для космического применения) и «Military» (для военного применения), а также сравнение с требованиями отечественных стандартов. Важную роль в определении понятия спецпартии сыграла международная кооперация при создании системы «Sesat» с 10-летним сроком активного существования и 12-летним техническим ресурсом. Данный спутник функционирует на орбите более 15 лет. В состав дополнительных испытаний обязательно входит оценка дрейфа значений параметров и контроль наличия посторонних частиц в подкорпусном пространстве изделий. Эти испытания проводятся в испытательном техническом центре. В результате спецпартии являются совместным продуктом завода-изготовителя и испытательного центра.
Разработка отдельного технологического процесса по изготовлению электронной компонентной базы для космической отрасли, требуя значительных вложений, делает невыгодной поставку малых партий изделий. Это положение совпадает с идеей комплектования всех аппаратур КА ЭКБ одинаково высокого уровня качества на принципе равнонадежности.
Алгоритмы метода жадных эвристик для задач автоматической группировки
В настоящей работе предполагается, что совокупность измерений (параметров) объектов одной группы (кластера) является многомерной случайной величиной, распределенной по некоторому известному закону распределения, при этом параметры этого распределения неизвестны. Суть рассматриваемой задачи группировки объектов состоит в том, чтобы отделить объекты, предположительно порожденные одним из распределений в этой смеси, от других. Традиционным инструментом при решении задач разделения смесей является метод максимального правдоподобия и соответствующий критерий – функция правдоподобия. Задача разделения смесей сводится к задаче максимизации этой функции. При этом искомыми параметрами функции правдоподобия являются параметры распределений [12].
Данные весьма высокой размерности (несколько сотен измерений) встречаются в задаче выделения однородных партий электронных изделий, например интегральных схем из сборной партии [2]. В такого рода задачах требуется получение не просто приемлемого результата, но очень точного и стабильного при многократных запусках. Например, такие задачи возникают при проверке качества состава (однородности/неоднородности) смеси однотипных микроэлектронных изделий [1] в космической промышленности. Разделение смеси на предполагаемые однородные партии производится на основе результатов интеллектуального анализа данных тестовых испытаний, которые представлены векторами данных очень большой размерности (сотни измерений) [2, 9].
Простой EM-алгоритм с двумя чередующимися шагами для разделения смеси распределений [13] в случае многомерных данных сильно зависит от начального решения.
Одной из хорошо зарекомендовавших себя стратегий глобального поиска является применение эволюционных (генетических) алгоритмов. Сложности кодирования решений, традиционно представляемых в классических генетических алгоритмах L-битными строками, в алгоритмах метода жадных эвристик [10] решены применением так называемого генетического алгоритма с вещественным алфавитом, в котором «особи» – промежуточные решения задач k-медиан или k-средних – представлены непосредственно множествами точек в пространстве Rd (то есть непосредственно множествами медиан или центроидов).
Алгоритм с гетерогенной популяцией для задачи разделения смеси распределений
1. Сгенерировать случайным образом NPOPнач начальных решений, представленных парой множеств распределений и их весовых коэффициентов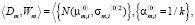 
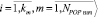. Начальные значения среднеквадратичных отклонений устанавливаются равными для всех кластеров и вычисляются для всей выборки: 
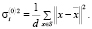Значения 
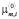устанавливаются равными координатам случайно выбранных векторов данных. Для каждого из начальных решений запускается EM-алгоритм, полученные значения целевой функции сохраняются в переменных 
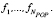Присвоить Niter = 0.
2. Niter = Niter + 1;
.
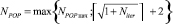Если NPOP изменилось, то инициализировать особь XNpop аналогично шагу 1. Выбрать случайным образом k1, k2∈[1, NPOP], k1 ≠ k2;
3. 
.
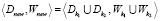4. Пока |Dnew| > pmax , выполнять: выбрать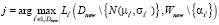 
;
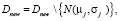
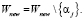Следующая итерация 4.
5. Выбрать случайным образом pchild∈{2, pmax}. Если pchild > |Dnew|, то pchild = |Dnew|.
6. 
.
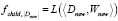7. Пока |Dnew| > pchild , выполнять: выбрать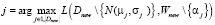 
;
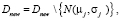
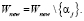Следующая итерация 7.
8. Пока |Dnew| > 2: Присвоить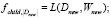 
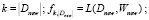если 
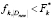, то присвоить 
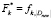; Выполнить шаги 4.1 и 4.2 для Dnew. Следующая итерация 8.
9. Выбрать j3∈{1, NPOP} с использованием турнирного замещения. Присвоить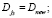 
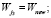
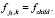
10. Проверить условия останова, перейти к шагу 2.
Результаты работы EM-алгоритма в режиме мультистарта и его модификаций обозначены EM, CEM, SEM (таблица 1, для 30 запусков алгоритмов).
Метод жадных эвристик [10] может быть успешно применен для построения эффективных алгоритмов решения задач разделения смеси распределений. При этом сохраняется важное свойство алгоритмов, полученных с применением данного подхода: высокая точность получаемых результатов. Для задачи автоматической группировки электрорадиоизделий [2, 9] новый алгоритм в ходе нескольких (не более 10) попыток запуска позволяет найти, вероятно, точный результат задачи или по крайней мере результат, который не получается превзойти с применением известных алгоритмов.
Получен новый алгоритм, стабильно превосходящий по точности получаемых результатов известные алгоритмы для некоторых классов задач, позволяющий получить решение сразу для серии задач разделения смеси распределений. В частности, таким классом задач являются задачи разделения смесей сферических и некоррелированных гауссовых распределений в пространствах большой размерности (десятки-сотни измерений) с числом векторов данных от сотен до десятков тысяч.
Моделирование сборной партии электрорадиоизделий в виде смеси многомерных гауссовских распределений по результатам неразрушающих испытаний
Тестовый центр исходит из предположения о том, что результаты РФА распространяются на всю исследуемую партию ЭРИ. Данное предположение имеет основания лишь в случае, если партия ЭРИ изготовлена как единая производственная партия и из единой партии пластин. Иначе же различия в составе и технологии изготовления полупроводникового сырья (трещины, поры, вкрапления), а также возможные флуктуации в технологическом процессе и нарушения технологии при изготовлении отдельных производственных партий ставят под сомнение выводы проведенного РФА.
Исследуем возможность попадания ЭРИ, не прошедших РФА, в партию, поставляемую для комплектования электронной аппаратуры с особыми требованиями качества. Пусть исследуемая партия включает N ЭРИ и состоит из k однородных партий объемом N1,N2,…Nk штук, при этом одна из партий имеет дефекты, которые могут быть выявлены при РФА. Без потери общности предположим, что первая партия – дефектная. Для проведения РФА случайным образом выбираются NРФА штук изделий. Пусть N = 40, N1 = 10, N2 = N3 = 15.
Вероятность того, что для РФА не будет отобран хотя бы один экземпляр первой дефектной партии, и РФА сборной партии ошибочно покажет отсутствие дефектов, составит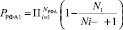 
.
Технологическим процессом тестового центра предусмотрено, что для РФА отбираются 3 изделия. Тогда вероятность того, что элементы из первой дефектной партии не будут отобраны для РФА, составит
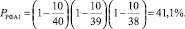
Разбор партии на однородные по составу группы позволит существенно увеличить эффективность проводимого РФА. В приведенном примере количество изделий, подвергаемых РФА, остается неизменным, если отбирать по одному изделию из каждой однородной группы. Если группы при этом определены корректно, вероятность изделий из партий, не прошедших РФА, снижается до нуля.
Сравнительные результаты серийного алгоритма
|
Набор данных, число вектор., размерн. |
Число класт. k, тип распр., время |
Алгоритм |
Ср. рез-т (лог. ф-ция пр-подобия) |
Ср. кв. откл. результатов |
|
Europe (UCI), N = 169308, d = 2 |
40, сфер, 1,5 часа |
Новый EM CEM SEM |
–3625694,1* –3625957,3 –3625779,0 –3625740,2 |
20,148 49,561 25,064 29,064 |
|
Тесты ИС 1526ТЛ1, N = 1234, d = 120 |
5, сфер., 5 сек. |
Новый EM |
3673,671* 3598,160 |
44,043 32,160 |
Примечание.* – лучший результат.
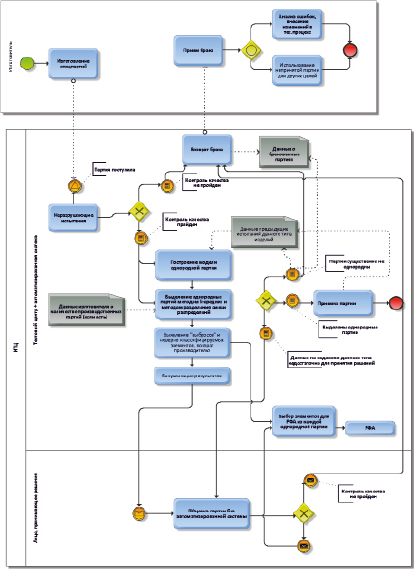
Обновленная BPMN-схема процесса формирования спецпартии электронной компонентной космического применения (ЭКБ)
Если метод разделения сборных партий ЭРИ обеспечивает их разделение с вероятностью ошибки Pош, то вероятность того, что дефектная однородная партия не пройдет РФА при NРФА = k составит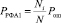 
, что для приведенного выше примера составит 2,5 % даже при уровне ошибок классификации в 10 %. Таким образом, даже при высоком уровне ошибок методы разделения сборной партии повышают ценность РФА.
Автоматическое определение числа однородных групп (кластеров) – одна из труднейших задач интеллектуального анализа данных. Алгоритмы автоматической группировки запускаются при различных предположениях о числе групп, наилучшее значение выбирается на основании некоторого критерия компактности и взаимной удаленности выявленных групп в нормированном пространстве. Критерий силуэта [14] изначально был создан как средство интерпретации и подтверждения результатов автоматической группировки данных. Он пригоден к использованию только при условии наличия двух или более кластеров в исследуемых данных. Следует провести оценку распределений частот и плотностей числовых характеристик на наличие многомодальности, что укажет на возможность разделения исходной выборки на группы, сходные по характеристикам объектов.
Общая схема принятия решений по приемке партий электрорадиоизделий
В рамках исследовательской работы была обновлена схема метода принятия решений по комплектации электронных узлов космических аппаратов. На рисунке приведена BPMN-схема принятия решения о приемке спецпартии, в которую включен этап выделения однородных партий методом разделения смеси распределений.
Для повышения надежности программных модулей систем управления, участвующих в принятии решения, целесообразно использовать методы повышения отказоустойчивости [9]. В частности, мы дополняем действующую систему автоматической группировки электрорадиоизделий по однородным производственным партиям на основе модели k-средних программной подсистемой на основе модели разделения смеси распределений. Такой подход позволяет обеспечить лицо, принимающее решения о приемке партий и о направлении их экземпляров на разрушающий физический анализ, дополнительной информацией. Одна модель кластеризации позволяет верифицировать результаты другой модели, а при несовпадении результатов в условиях повышенных требований к качеству, предъявляемых космической промышленностью, предлагается отказаться от использования спорных экземпляров изделий при комплектовании бортовой аппаратуры.
Выводы
Показано, что анализ партий электронной компонентной базы на однородность является актуальной задачей в случае ЭРИ с высоким уровнем интеграции, где флуктуации технологического процесса могут привести к существенным ошибкам в оценке качества и физических характеристик ЭРИ, в том числе – радиационной стойкости. Также приведено обоснование необходимости создания специальных партий (спецпартий) электрорадиоизделий для централизованной комплектации аппаратуры [5].
На примере задачи выявления однородных производственных партий ЭРИ из сборной партии по данным неразрушающих тестовых испытаний показано, что новая методика позволяет снизить процент ошибок при выявлении однородных партий.
Библиографическая ссылка
Орлов В.И., Сташков Д.В., Казаковцев Л.А., Рожнов И.П., Казаковцева О.Б., Насыров И.Р. УСОВЕРШЕНСТВОВАННАЯ МЕТОДИКА ФОРМИРОВАНИЯ ПАРТИЙ ЭЛЕКТРОННОЙ КОМПОНЕНТНОЙ БАЗЫ С ОСОБЫМИ ТРЕБОВАНИЯМИ КАЧЕСТВА // Современные наукоемкие технологии. – 2018. – № 1. – С. 37-42;URL: https://top-technologies.ru/ru/article/view?id=36889 (дата обращения: 03.12.2024).