Распределение случайных точек внутри произвольной фигуры на плоскости или в пространстве является актуальной проблемой не только в вычислительной и стохастической геометрии, но и в математическом моделировании, численных методах, компьютерной графике [1–4]. Больший интерес представляет равномерное распределение точек, которое связано не только с вычислительными задачами, решаемыми, например, методом Монте-Карло, но и с многочисленными техническими, биологическими и экономическими приложениями [5, 6]. В последние годы активно разрабатываются программные продукты для работы с моделями карт, для проектирования ландшафтов и экологического моделирования, содержащие инструменты для случайного расположения объектов (например, для территориального распределения лесных массивов на картах и др.) [7, 8]. Однако в использовании таких систем, в частности при работе с инструментами случайного распределения точек (объектов на картах), существуют определенные неудобства. Например, на сайте Geospatial Modelling Environment [8] указано, что программа может достаточно долго выполнять распределение случайных объектов, если область на карте имеет малую площадь и большой периметр. Такая же ситуация возможна и при работе с инструментами в профессиональном картографическом программном обеспечении ArcGIS Pro [7]. В обеих системах алгоритмы используют циклы с постусловием: случайные точки внутри некоторой выпуклой оболочки, содержащей выбранную область (на карте), генерируются до тех пор, пока внутрь этой области не попадет заданное количество точек. Очевидно, что если площадь выбранной области мала по сравнению с площадью ее выпуклой оболочки, то количество шагов такого алгоритма может быть велико.
Существуют различные алгоритмические подходы к решению этой проблемы [3, 5, 6, 9]. Вариативность подходов и эффективное решение этой проблемы стало возможным благодаря активному использованию информационно-коммуникационных технологий, специализированным программным продуктам (например, пакетам компьютерной математики). Сочетание ИКТ и наглядности геометрических подходов в решении таких задач дает определенные преимущества [5, 6, 10, 11].
В данной статье показаны геометрические приемы для построения и реализации алгоритма генерации случайных точек внутри произвольных многоугольников и многогранников. Они позволяют избавиться от «холостого хода» алгоритма, возникающего при использовании цикла с постусловием «пока не будет получено необходимое количество точек». Преимущества использования этих геометрических приемов особенно проявляются для невыпуклых многоугольников, площадь которых значительно меньше площади их выпуклой оболочки, и для невыпуклых многогранников, объем которых также значительно меньше объема их выпуклой оболочки.
Генерация случайных точек внутри произвольных многоугольников и многогранников
Мы рассматриваем следующие задачи.
Задача 1. Произвольный многоугольник P площади S задан координатами своих вершин на плоскости. Требуется равномерно распределить внутри него n случайных точек. Уточним постановку задачи. Требуется построить последовательность Dn(n∈N), такую, что:
1) Dn является n-элементным множеством точек плоскости и 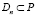 ;
;
2) для любого треугольника 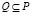 площадью S(Q) обозначим посредством k(Q, n) количество точек из Dn, попавших внутрь Q. Требуется, чтобы
площадью S(Q) обозначим посредством k(Q, n) количество точек из Dn, попавших внутрь Q. Требуется, чтобы 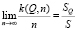 .
.
В общем случае решение поставленной задачи подразумевает построение какой-либо триангуляции данного многоугольника и «равномерное заполнение» точками каждого из треугольников. При этом генерируются две последовательности независимых случайных чисел si и ti) (i = 1,…, n), равномерно распределенных на интервале (0, 1). В этом случае точки с координатами (si, ti) равномерно распределены внутри единичного квадрата. Если задать на плоскости произвольные точки A, B, то точки с координатами
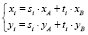
будут равномерно распределены внутри параллелограмма со сторонами OA, OB.
Однако для равномерного распределения точек внутри треугольника OAB требуется проверять условие si + ti ≤ 1. Выгоднее изначально равномерно распределить точки внутри прямоугольного треугольника с единичными катетами, гипотенуза которого совпадает с диагональю квадрата (так как это позволяет избавиться от проверки условия si + ti ≤ 1). Мы предлагаем следующее решение задачи 1.
Пусть сгенерированы две последовательности независимых случайных чисел si и ti (i = 1,…, n), равномерно распределенных на интервале (0, 1). Построим последовательность точек с координатами
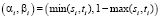
(эти точки равномерно распределены внутри прямоугольного треугольника с единичными катетами (см. пример на рис. 1 слева)). Тогда (фактически выполнив аффинное преобразование) получим, что случайные точки M(xi, yi) с координатами
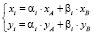
равномерно распределены внутри произвольного треугольника OAB (см. пример на рис. 1 справа). Несложно записать формулы для координат случайных точек внутри произвольного треугольника ABC.
Важным моментом в равномерном распределении случайных точек внутри произвольного многоугольника является определение количества точек внутри каждого треугольника в построенной триангуляции (ее всегда можно построить, взяв в качестве узлов только вершины многоугольника).
Мы предлагаем распределить необходимое количество точек n, не пользуясь определением и приближенными равенствами, а явным образом, используя геометрические приемы. Для построения равномерного распределения мы предлагаем следующий алгоритм:
1. Пронумеруем все треугольники в триангуляции (обозначим их количество k) и найдем площадь каждого из них: S1, S2,…, Sk (площадь многоугольника обозначим S).
2. Построим разбиение отрезка [0, S] точками S1, S1 + S2, …, S1 + S2 + … + Sk-1.
3. Сгенерируем последовательность n случайных чисел ξi, равномерно распределенных на интервале (0, 1), и составим последовательность ξi•S.
4. Количество точек mk внутри k-го треугольника будет равно числу точек вида ξi•S, попавших в k-й промежуток разбиения в п. 2). Очевидно, что 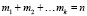 .
.
На рис. 2 показан пример распределения случайных точек внутри невыпуклого многоугольника. Построение выполнено в MATLAB с помощью алгоритма, реализованного с учетом представленных в работе геометрических подходов.
Рассмотрим задачу о равномерном распределении точек внутри произвольного многогранника.
Задача 2. Произвольный многогранник P объема V в пространстве задан координатами своих вершин. Требуется равномерно распределить внутри него n случайных точек.
Аналогично задаче 1 уточним постановку задачи. Требуется построить последовательность Dn(n∈N), такую что:
1) Dn является n-элементным множеством точек плоскости и 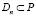 ;
;
2) для любого тетраэдра 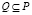 объемом V(Q) обозначим посредством k(Q, n) количество точек из Dn, попавших внутрь Q. Требуется, чтобы
объемом V(Q) обозначим посредством k(Q, n) количество точек из Dn, попавших внутрь Q. Требуется, чтобы 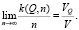
В общем случае решение поставленной задачи подразумевает построение какой-либо трехмерной триангуляции данного многогранника (разбиение на тетраэдры) и равномерное «заполнение» точками каждого тетраэдра в разбиении. При этом генерируются три последовательности независимых случайных чисел si, ti и ri (i = 1,…, n), равномерно распределенных на интервале (0, 1). Известно, что в этом случае точки с координатами (si, ti, ri) равномерно распределены внутри единичного куба.
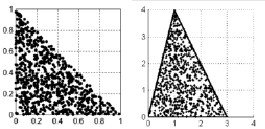
Рис. 1. Пример равномерного распределения 750 случайных точек (αi, βi) внутри прямоугольного треугольника (слева) и соответствующее ему распределение точек M(xi, yi) внутри треугольника OAB (где A (1, 4) и B (3, 0))
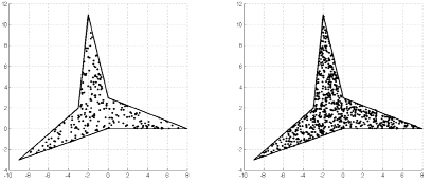
Рис. 2. Полученное с помощью предложенного алгоритма случайное распределение 250 (слева) и 750 (справа) точек внутри многоугольника
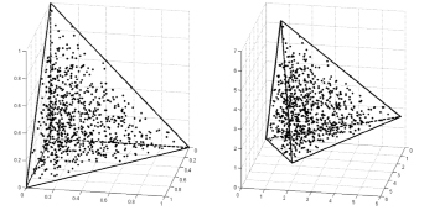
Рис. 3. Пример равномерного распределения 750 случайных точек (αi, βi, γi) внутри тетраэдра, образованного векторами 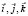 (слева), и соответствующее ему распределение точек M(xi, yi, zi) внутри тетраэдра OABC (где A (5, 2, 1), B (1, 6, 2) и C (2, 1, 7))
(слева), и соответствующее ему распределение точек M(xi, yi, zi) внутри тетраэдра OABC (где A (5, 2, 1), B (1, 6, 2) и C (2, 1, 7))
Рассмотрим в пространстве произвольные точки A, B, C (общего положения). Тогда точки M(xi, yi, zi) с координатами
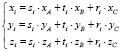
будут равномерно распределены внутри параллелепипеда с ребрами OA, OB, OC.
Мы предлагаем следующее решение задачи о равномерном распределении n точек внутри тетраэдра OABC.
Зададим точки с координатами
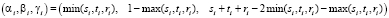 .
.
Эти точки равномерно распределены внутри тетраэдра, образованного векторами 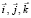 (см. пример на рис. 3 слева). Тогда (по существу выполнив аффинное преобразование) случайные точки M(xi, yi, zi) с координатами
(см. пример на рис. 3 слева). Тогда (по существу выполнив аффинное преобразование) случайные точки M(xi, yi, zi) с координатами
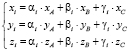
будут равномерно распределены внутри произвольного тетраэдра OABC (см. пример на рис. 3 справа). Несложно записать формулы для координат случайных точек внутри произвольного тетраэдра ABCD.
Опишем алгоритм равномерного распределения n случайных точек внутри произвольного многогранника в построенной трехмерной триангуляции (ее всегда можно построить, взяв в качестве узлов только вершины многогранника).
Как и при решении задачи 1, мы предлагаем распределить необходимое количество точек n, не пользуясь определением и приближенными равенствами, а явным образом, избегая холостого хода алгоритма при проверке условия принадлежности точки многограннику. Алгоритм аналогичен приведенному выше для задачи 1 и включает в себя выполнение следующих шагов.
1. Пронумеруем все тетраэдры в триангуляции (обозначим их количество k) и найдем объем каждого из них: V1, V2,…, Vk (объем многогранника обозначим V).
2. Построим разбиение отрезка 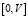 точками V1, V1 + V2, …, V1 + V2 + … + Vk-1.
точками V1, V1 + V2, …, V1 + V2 + … + Vk-1.
3. Сгенерируем последовательность n случайных чисел ξi, равномерно распределенных на интервале (0, 1), и составим вспомогательную последовательность ξi•V.
Результаты вычислительного эксперимента в примере 1
|
Номер эксперимента |
№ 1 |
№ 2 |
№ 3 |
№ 4 |
№ 5 |
№ 6 |
№ 7 |
|
Число точек n |
750 |
1000 |
3000 |
5000 |
10000 |
50000 |
10000 |
|
n1/n |
0,123 |
0,130 |
0,125 |
0,124 |
0,123 |
0,124 |
0,126 |
|
n2/n |
0,112 |
0,123 |
0,122 |
0,127 |
0,122 |
0,125 |
0,125 |
|
n3/n |
0,128 |
0,131 |
0,129 |
0,122 |
0,125 |
0,125 |
0,124 |
|
n4/n |
0,241 |
0,216 |
0,222 |
0,226 |
0,223 |
0,223 |
0,222 |
4. Количество точек mk внутри k-го тетраэдра будет равно числу точек вида ξi•V, попавших в k-ый промежуток разбиения в п. 2). Очевидно, что будет выполняться равенство 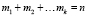 .
.
Пример 1. Будем распределять n случайных точек внутри тетраэдра, образованного векторами 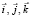 , объем которого V = 1/6. Обозначим V1 – объем тетраэдра, отсекаемого от исходного плоскостью x = 1/2, V2 – объем тетраэдра, отсекаемого от исходного плоскостью y = 1/2, V3 – объем тетраэдра, отсекаемого от исходного плоскостью z = 1/2, V4 – объем куба с ребром 1/3, три смежных ребра которого выходят из начала координат. Число точек, попавших в отсекаемые тетраэдры, обозначим соответственно n1, n2, n3, а в куб – n4. Очевидно, что V1 = V2 = V3 = 1/48, V4 = 1/27.
, объем которого V = 1/6. Обозначим V1 – объем тетраэдра, отсекаемого от исходного плоскостью x = 1/2, V2 – объем тетраэдра, отсекаемого от исходного плоскостью y = 1/2, V3 – объем тетраэдра, отсекаемого от исходного плоскостью z = 1/2, V4 – объем куба с ребром 1/3, три смежных ребра которого выходят из начала координат. Число точек, попавших в отсекаемые тетраэдры, обозначим соответственно n1, n2, n3, а в куб – n4. Очевидно, что V1 = V2 = V3 = 1/48, V4 = 1/27.
В таблице показаны отношения n1/n, n2/n, n3/n, n4/n (с точностью до 0,001) для числа случайных точек n = 750, 1000, 3000, 5000, 10000, 50000, 100000. Предельные отношения соответственно равны 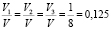 и
и 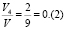 . Вычислительный эксперимент выполнен в MATLAB.
. Вычислительный эксперимент выполнен в MATLAB.
Заключение
Предложенные в работе геометрические приемы позволяют упростить построение и реализацию алгоритма генерации случайных точек, равномерно распределённых внутри произвольных многоугольников и многогранников, явно определять число шагов для получения необходимого числа точек. Приведенные примеры демонстрируют преимущества такого подхода.
Работа выполнена при финансовой поддержке ФГБОУ ВО «КГПУ им. В.П. Астафьева» по договору о выполнении НИР от 21.06.2017 г. № 16-746.
Библиографическая ссылка
Мартынова Е.В., Нигматулин Р.М. ГЕОМЕТРИЧЕСКИЕ ПРИЕМЫ В РЕАЛИЗАЦИИ АЛГОРИТМА ГЕНЕРАЦИИ СЛУЧАЙНЫХ ТОЧЕК ВНУТРИ ПРОИЗВОЛЬНЫХ МНОГОУГОЛЬНИКОВ И МНОГОГРАННИКОВ // Современные наукоемкие технологии. 2018. № 1. С. 27-31;URL: https://top-technologies.ru/ru/article/view?id=36887 (дата обращения: 13.03.2026).



