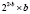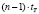Система остаточных классов (СОК) – это непозиционная система счисления, которая позволяет заменить последовательные методы выполнения арифметических операций над «длинными» целыми числами в позиционных системах счисления на параллельные методы выполнения арифметических операций над наборами «коротких» целых чисел [1–3]. Преимуществом СОК является простота выполнения операций сложения, вычитания, умножения (так называемых модульных операций) по сравнению с арифметикой в позиционных системах счисления, а существенным недостатком – сложность выполнения немодульных операций, таких как операции масштабирования, деления, определения знака, сравнения и определения переполнения диапазона представления чисел и т.д. Другим существенным преимуществом вычислений с применением СОК является более простая аппаратно-техническая реализация вычислительных устройств и, как следствие, их более низкое энергопотребление по сравнению с устройствами на основе вычислений в позиционных системах счисления. Учитывая особенности организации вычислений в СОК, их применение наиболее эффективно для решения задач, алгоритмизация которых реализована с существенным преобладанием модульных операций, например, задач цифровой обработки сигналов [4, 5], криптографии [6, 7].
Одной из важных и сложно реализуемых операций является операция расширения базиса СОК, которая необходима для выполнения операций расширения диапазона представления чисел, например, при реализации алгоритма Монтгомери в приложениях криптографии [6, 7], деления и масштабирования [4, 8], контроля ошибок вычислений [9, 10].
Задача расширения базиса
Система остаточных классов является непозиционной системой счисления, в которой значения позиционного числа A число представлено набором n остатков 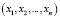 от деления числа A на каждый из n модулей
от деления числа A на каждый из n модулей 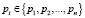 [1–3]:
[1–3]:
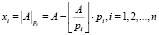 ,
,
где 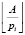 – целая часть частного
– целая часть частного 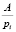 ,
, 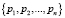 – набор оснований или базис СОК.
– набор оснований или базис СОК.
Произведение 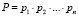 определяет диапазон представления чисел
определяет диапазон представления чисел 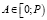 в СОК, причем, если все числа
в СОК, причем, если все числа 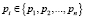 являются попарно взаимно простыми, то между любым положительным целым числом A из диапазона [0; P) и числом, представленным в СОК, имеется взаимно однозначное соответствие.
являются попарно взаимно простыми, то между любым положительным целым числом A из диапазона [0; P) и числом, представленным в СОК, имеется взаимно однозначное соответствие.
Расширение базиса, или смена базиса – это процедура, в которой осуществляется поиск значения 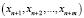 числа в СОК с новыми основаниями
числа в СОК с новыми основаниями 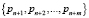 , представленного изначально в виде
, представленного изначально в виде 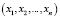 в СОК с основаниями
в СОК с основаниями 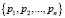 . Частным случаем является вычисление остатка от деления числа, представленного в СОК, по новому основанию pn+1. Для вычисления остатка от деления xn+1 числа, представленного в СОК, по новому основанию pn+1, используются два подхода: вычисление xn+1 с помощью Китайской теоремы об остатках (КТО) [11] и вычисление коэффициентов системы счисления со смешанными основаниями [2, 8, 12–15].
. Частным случаем является вычисление остатка от деления числа, представленного в СОК, по новому основанию pn+1. Для вычисления остатка от деления xn+1 числа, представленного в СОК, по новому основанию pn+1, используются два подхода: вычисление xn+1 с помощью Китайской теоремы об остатках (КТО) [11] и вычисление коэффициентов системы счисления со смешанными основаниями [2, 8, 12–15].
Система счисления со смешанными основаниями
Пусть 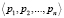 – упорядоченный набор оснований СОК. Тогда любое число, представленное в СОК упорядоченным набором остатков от деления
– упорядоченный набор оснований СОК. Тогда любое число, представленное в СОК упорядоченным набором остатков от деления 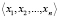 по соответствующим основаниям
по соответствующим основаниям 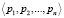 , может быть также представлено в системе счисления (СС) со смешанными основаниями, с базисом из n элементов
, может быть также представлено в системе счисления (СС) со смешанными основаниями, с базисом из n элементов 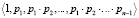 с коэффициентами
с коэффициентами  , такими, что для целого числа
, такими, что для целого числа 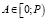 выполняется равенство
выполняется равенство
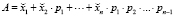 . (1)
. (1)
Точный метод определения остатка от деления по новому модулю, основанный на преобразовании числа в СССО, был предложен Сабо и Танакой [2]:
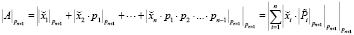 , (2)
, (2)
где 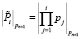 ,
, 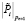 вычислены заранее и занесены в таблицу.
вычислены заранее и занесены в таблицу.
Таким образом, для вычисления остатка от деления по новому модулю pn+1 необходимо сначала вычислить коэффициенты СС со смешанными основаниями 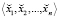 , затем вычислить остаток от деления по формуле (2).
, затем вычислить остаток от деления по формуле (2).
Вычислительная сложность методов расширения базиса на основе вычисления коэффициентов системы счисления со смешанными основаниями
Коэффициенты 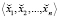 представления
представления 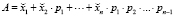 вычисляются следующим образом [2]:
вычисляются следующим образом [2]:
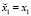 ,
,
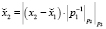 ,
,
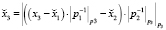 ,
,
…
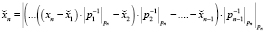 . (3)
. (3)
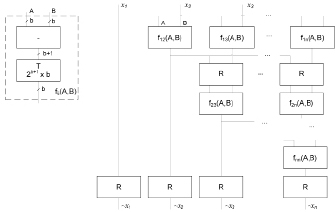
Рис. 1. Схема конвейеризированного метода Сабо и Танаки [14]
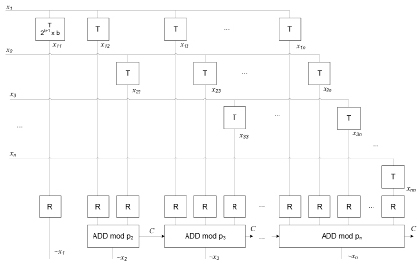
Рис. 2. Схема параллельного метода Хуанга [14]
Для вычисления коэффициентов по формулам (3) требуется выполнение 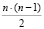 операций модулярного вычитания и столько же операций модулярного умножения [2].
операций модулярного вычитания и столько же операций модулярного умножения [2].
Методы, представленные в работах [12, 13], основаны на классических методах [2], имеющих сложность O(n2), и ориентированы на оптимизацию числа арифметических операций.
Параллельные методы [8, 14, 15] также основаны на классических методах [2] и позволяют сократить время вычисления коэффициентов 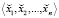 за счет введения дополнительных вычислительных устройств. Например, Хуангом [14] предложен конвейеризированный метод Сабо и Танаки [2] (рис. 1), а также параллельный алгоритм преобразования в систему счисления со смешанными основаниями, использующий дополнительные подстановочные таблицы (рис. 2). На рисунках использованы следующие обозначения: R – регистр для хранения промежуточных результатов, fij – функциональный блок, состоящий из вычитателя («–») и таблицы (T), T – подстановочная таблица, С – каналы передачи единиц переноса, ADD mod pi – каскадные сумматоры по модулю pi.
за счет введения дополнительных вычислительных устройств. Например, Хуангом [14] предложен конвейеризированный метод Сабо и Танаки [2] (рис. 1), а также параллельный алгоритм преобразования в систему счисления со смешанными основаниями, использующий дополнительные подстановочные таблицы (рис. 2). На рисунках использованы следующие обозначения: R – регистр для хранения промежуточных результатов, fij – функциональный блок, состоящий из вычитателя («–») и таблицы (T), T – подстановочная таблица, С – каналы передачи единиц переноса, ADD mod pi – каскадные сумматоры по модулю pi.
В [14] время выполнения представлено как 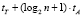 (где tT – время выборки из таблицы, tA – время выполнения операции сложения), что, как было показано в [8], не достигается в связи с формированием переносов. Данный метод был улучшен в [8] за счет введения дополнительных
(где tT – время выборки из таблицы, tA – время выполнения операции сложения), что, как было показано в [8], не достигается в связи с формированием переносов. Данный метод был улучшен в [8] за счет введения дополнительных 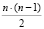 умножителей, сложность алгоритма при этом показана как O(log n). Схема формирования коэффициентов СС со смешанными основаниями [8] представлена на рис. 3. Использованы следующие обозначения: mij – значения коэффициентов СС со смешанными основаниями для чисел
умножителей, сложность алгоритма при этом показана как O(log n). Схема формирования коэффициентов СС со смешанными основаниями [8] представлена на рис. 3. Использованы следующие обозначения: mij – значения коэффициентов СС со смешанными основаниями для чисел 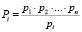 , вычислены заранее и хранятся в таблицах, *i – умножители по модулю pi, ADD mod pi – каскадные сумматоры по модулю pi, С – каналы передачи единиц переноса, ADD – позиционный двоичный каскадный сумматор для формирования старшей единицы переноса.
, вычислены заранее и хранятся в таблицах, *i – умножители по модулю pi, ADD mod pi – каскадные сумматоры по модулю pi, С – каналы передачи единиц переноса, ADD – позиционный двоичный каскадный сумматор для формирования старшей единицы переноса.
Алгоритм Чакраборти и др. [15] использует каскадную схему подстановочных таблиц и сумматоров, при этом таблицы имеют два входа и два выхода, таким образом, таблиц в общей сложности требуется меньше. При конвейерной обработке время преобразования равно времени выборки из таблицы плюс время одного модулярного сложения. Метод хорошо работает для разрядности модулей 4–6 бит, поскольку при большей разрядности значительно увеличивается объем подстановочных таблиц. Параллельный алгоритм Миллера и МакКормика [15] использует только подстановочные таблицы и основан на решении линейных диофантовых уравнений. Алгоритм медленнее, чем [14], однако он не требует дополнительных арифметических устройств, и в случае конвейерной обработки время одного преобразования равно времени выборки из таблицы.
В таблице представлены следующие характеристики наиболее быстрых методов вычисления коэффициентов СС со смешанными основаниями [2, 8, 14, 15]: количество и объем требуемых подстановочных таблиц, сумматоров/вычитателей (ADD/SUB) и модулярных умножителей (MUL), а также время выполнения; при этом использованы следующие обозначения: n – количество модулей, tT – время выборки из таблицы, tA – время выполнения операции сложения/вычитания, tM – время выполнения операции умножения.
Характеристики методов вычисления коэффициентов СССО
|
Метод |
Количество и объем таблиц |
ADD/SUB |
MUL |
Время вычисления
|
|
Сабо, Танака [2], классические |
– |
|
|
|
|
Сабо, Танака [2], конвейеризированный |
|
|
– |
|
|
Хуанг [14] |
|
|
– |
|
|
Хитц, Калтофен [8] |
|
|
|
|
|
Чакраборти и др. [15], последовательный |
|
|
– |
|
|
Чакраборти и др. [15], параллельный |
|
|
– |
|
|
Миллер [15] |
|
– |
– |
|
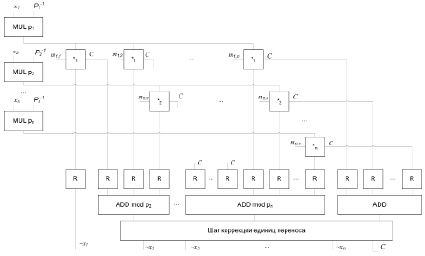
Рис. 3. Схема работы алгоритма Хитц, Калтофен [8]
Как видно из таблицы, самые быстрые методы вычисления коэффициентов СС со смешанными основаниями требуют O(n2) арифметических устройств и подстановочных таблиц, время же вычисления коэффициентов ограничивается O(log n).
Вычисление остатка от деления по формуле (2) требует n модулярных умножителей, работающих параллельно и (n – 1) модулярных сумматоров, включенных по каскадной схеме, при этом время вычисления составляет 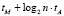 [8] или один модулярный умножитель с накоплением (состоящий из одного умножителя по модулю, одного сумматора по модулю и регистра для хранения промежуточного результата), время при этом составляет
[8] или один модулярный умножитель с накоплением (состоящий из одного умножителя по модулю, одного сумматора по модулю и регистра для хранения промежуточного результата), время при этом составляет 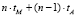 . Общее время выполнения операции расширения базиса методом [8] составляет
. Общее время выполнения операции расширения базиса методом [8] составляет 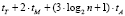 , при этом для его реализации потребуется
, при этом для его реализации потребуется 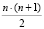 подстановочных таблиц,
подстановочных таблиц, 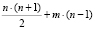 модулярных сумматоров/вычитателей,
модулярных сумматоров/вычитателей, 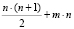 модулярных умножителей, m – количество дополнительных модулей, на которые необходимо расширить базис.
модулярных умножителей, m – количество дополнительных модулей, на которые необходимо расширить базис.
Заключение
Для преобразования числа x1,x2,…,xn, представленного в СОК с основаниями 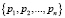 к xn+1 ,xn+2, …, xn+m в СОК с основаниями pn+1, pn+2, …, pn+m, необходимо вычислить коэффициенты СС со смешанными основаниями
к xn+1 ,xn+2, …, xn+m в СОК с основаниями pn+1, pn+2, …, pn+m, необходимо вычислить коэффициенты СС со смешанными основаниями 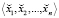 , затем m раз вычислить остатки от деления по модулям pn+1, pn+2, …, pn+m по формуле (2). Вычисления остатка от деления по каждому модулю независимы и могут быть выполнены параллельно.
, затем m раз вычислить остатки от деления по модулям pn+1, pn+2, …, pn+m по формуле (2). Вычисления остатка от деления по каждому модулю независимы и могут быть выполнены параллельно.
В качестве дальнейшего направления исследований планируется разработка метода расширения базиса, имеющего оптимальное соотношение времени выполнения и аппаратных затрат, основанного на том, что при вычислении коэффициентов СС со смешанными основаниями на каждом шаге последовательно вычисляется очередной разряд 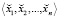 , который может сразу же использоваться для вычисления остатка по формуле (2). Таким образом, можно совместить во времени процесс получения коэффициентов
, который может сразу же использоваться для вычисления остатка по формуле (2). Таким образом, можно совместить во времени процесс получения коэффициентов 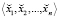 и вычисления остатков от деления.
и вычисления остатков от деления.
Методы расширения базиса, основанные на вычислении коэффициентов системы счисления со смешанными основаниями, наиболее целесообразно использовать для массового выполнения операций расширения базиса, полной или частичной смены базиса. Для вычисления единичного остатка от деления по новому основанию лучше выбирать способы, позволяющие максимально быстро вычислить остаток, например, [8], или методы, основанные на Китайской теореме об остатках [11]. В случае использования метода [8] необходим дополнительный анализ целесообразности его использования, поскольку аппаратные затраты для его реализации достаточно велики.
Библиографическая ссылка
Коржавина А.С., Князьков В.С. МЕТОДЫ РАСШИРЕНИЯ БАЗИСА В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ: ОБЗОР И АНАЛИЗ ВЫЧИСЛИТЕЛЬНОЙ СЛОЖНОСТИ // Современные наукоемкие технологии. 2017. № 12. С. 37-42;URL: https://top-technologies.ru/ru/article/view?id=36868 (дата обращения: 01.02.2026).




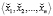
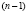
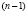
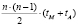
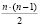 ,
, 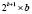
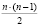
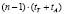
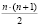 ,
, 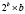
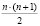
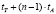
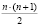 ,
, 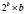
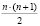
 ,
, 
 ,
, 
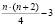
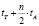
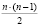 ,
,