При проведении экспериментов по численному моделированию МСС большое значение отводится построению ГС. Они создаются на основе результатов решения и отражают его точность. Коммерческие программные средства (ПС), предназначенные для постановки экспериментов по численному моделированию, такие как ANSYS, ТЕСИС, ESI GROUP, имеют встроенные средства для построения ГС. Свободно распространяемые пакеты, в частности OpenFOAM, по возможностям не уступают коммерческим аналогам, но не имеют графической оболочки для взаимодействия с пользователем. Вся работа с проектом задачи осуществляется посредством командной строки, что усложняет постановку экспериментов, так как требует значительных затрат времени при подготовке проекта задачи и запоминания значительного количества консольных команд.
Создание интерфейсов для ПС OpenFOAM представляет интерес для разработчиков. Так были разработаны графические оболочки SALOME и Helyx OS. Несмотря на это, некоторые отечественные промышленные предприятия делают выбор в пользу создания собственных программных продуктов, учитывающих специфику работы предприятия и требования к возможностям программного обеспечения.
Авторами настоящей статьи предложен собственный вариант графического интерфейса пользователя на базе языка программирования Python 3.4 и библиотеки PyQt4, которая представляет собой расширение языка Python для графического кросплатформенного фреймворка Qt. Подход к созданию данного продукта описан в работе [1], а устройство и функционирование главного окна интерфейса – в работе [2]. Представленный графический интерфейс разработан для специалистов АО «ГРЦ Макеева» в г. Миассе и подтвержден свидетельством о государственной регистрации программы для ЭВМ № 2016613637 от 01.04.2016, выданным организацией «Федеральный институт промышленной собственности».
Настоящая статья расширяет список возможностей продукта путем внедрения модуля для построения ГС решения задачи МСС. При этом к инструментам разработки кроме вышеуказанных технологий относится библиотека Matplotlib, отвечающая за визуализацию двумерных графических объектов, и библиотека NumPy, обеспечивающая возможность выполнения математических операций с многомерными массивами.
Цель работы состоит в создании программного модуля, позволяющего выполнять построение ГС по итогам решения задачи МСС. В рамках реализации поставленной цели предполагается решение комплекса задач: выбор определенной задачи МСС и изучение ее особенностей, моделирование выбранной задачи МСС в ПС OpenFOAM, изучение возможностей библиотек Matplotlib и NumPy на основе документации [3, 4], написание программного кода модуля.
Предполагаемым результатом работы является подключение разработанного модуля к графической оболочке, описанной в статье [1], выполнение моделирования выбранной задачи в этой графической оболочке и тестирование работы модуля после завершения моделирования. Должно быть предусмотрено автоматизированное выполнение кода данного программного модуля по завершению решения задачи, а также его выполнение при нажатии пользователем соответствующей кнопки панели инструментов главного окна.
Авторами настоящей статьи предложен подход, согласно которому данные для построения графика извлекаются из служебного файла с расширением «.log». В соответствии с логикой работы графического интерфейса, описанного в статье [1], все выходные данные, генерируемые в процессе решения задачи МСС, автоматически записываются в служебный log-файл. Для извлечения данных из файла применяются конструкции на базе шаблонов языка программирования Python 3.4 [5].
Необходимо отметить, что количество графиков на одной координатной оси определяется количеством коэффициентов, значения которых записываются в определенный момент времени (итерацию) в log-файл. При этом имена коэффициентов на каждой итерации неизменны. Таким образом, каждой итерации в log-файле соответствует информационный блок, где каждому коэффициенту предшествует служебный оператор «for».
Из каждого итерационного блока необходимо извлечь значение параметра «Time». Далее на основе полученных значений формируется массив, каждый элемент которого представляет собой определенное значение, откладываемое на оси OX. Каждому значению параметра «Time» ставится в соответствие значение определенного коэффициента, например скалярных величин Ux и Uy для параметра «Скорость» (U). Значение каждого коэффициента извлекается из его свойства «Final residual» и также помещается в массив, соответствующий этому коэффициенту. На основе сформированных массивов откладываются значения на оси OY. Таким образом, формируются исходные данные для всех ГС.
Авторами предложено использование библиотеки NumPy для преобразования сформированных массивов строковых данных в формат, допустимый для построения графических объектов и библиотеки Matplotlib, предоставляющей необходимые для построения ГС инструменты. Принято решение использовать для вывода сформированных графических объектов стандартный виджет библиотеки PyQt4 [6], реализующий функции окна (класс QWidget).
В качестве примера задачи МСС, на которой демонстрируются особенности разработки и тестирования модуля, приведена задача численного моделирования эволюции границы каверны при пуске торпеды [7], подготовленная специалистами АО «ГРЦ Макеева».
Описание структуры модуля
На рис. 1 представлена UML-диаграмма, демонстрирующая взаимосвязь компонентов модуля построения ГС. В основном классе – «GraphWindow», соответствующем окну модуля, осуществляется вызов всех функций, необходимых для построения ГС. Класс «Graphs_Data» содержит объявления функций и их программный код. Данный класс наследует свойства служебного класса «Graph_Canvas» (холст графика). Вынесение его в отдельный файл позволяет использовать один и тот же холст при построении ГС для других решателей, что снижает избыточность кода.
Для извлечения данных из log-файла необходимо получить доступ к этому файлу, т.е. необходимо наличие переменной, которая бы содержала абсолютный путь. Такая переменная передается в окно модуля из главного окна, но поскольку при расширении возможностей интерфейса может возникнуть потребность вновь получить значение абсолютного пути, имеет смысл в отдельном служебном файле создать специальный класс (fd_class), который бы содержал эту переменную. Таким образом, при ее передаче из главного окна она сначала будет записываться в этот служебный класс (путем вызова соответствующей функции класса), а затем можно обратиться к этой переменной из любого другого модуля (путем вызова соответствующей функции служебного класса).
Описание программного кода компонентов модуля
Инструкции, содержащиеся в листинге 1, отвечают за создание холста (поверхности) для рисования графиков и координатных осей. Каждый график может быть отображен на отдельной системе координат или на общей.
Листинг 1. Программный код холста для построения ГС (Graph_Canvas.py)
from matplotlib.backends.backend_qt4agg import FigureCanvasQTAgg as GOCCanvas
from matplotlib.figure import Figure
class Graph_Canvas(GOCCanvas):
def __init__(self, parent=None):
GBox = Figure()
self.axes = GBox.add_subplot(111)
GOCCanvas.__init__(self, GBox)
В библиотеке Matplotlib в рамках реализации концепции поверхности для рисования (холста) графических объектов применяется класс FigureCanvasQTAgg. Фактически он представляет собой «бумагу», на которой можно разместить любое количество контейнеров верхнего уровня (класс Figure), объединяющих все составляющие графика. Метод add_subplot позволяет добавить в контейнер верхнего уровня Figure контейнер для графиков. Аргументы метода определяют количество систем координат. В последней строке листинга 1 происходит вызов конструктора базового класса (GOCCanvas) с передачей ссылки на контейнер Figure, для которого необходимо установить холст.
Листинг 2. Программный код окна модуля для построения ГС (Graph_Window.py)
from add_classes.fd_class import fd_class
from add_classes.Graph_Canvas import Graphs_Data
class Graph_Window(QtGui.QWidget):
def __init__(self, fd, parent=None):
QtGui.QWidget.__init__(self, parent)
fd_class.post_fd(fd)
GD = Graphs_Data()
GD.getting_initial_data()
GD.t_making()
GD.Ux_making()
GD.graphs_making()
GW_hbox = QtGui.QHBoxLayout()
GW_hbox.addWidget(GD)
GW_form = QtGui.QFormLayout()
GW_form.addRow(GW_hbox)
self.setLayout(GW_form)
Класс, представленный в листинге 2, соответствует стандартному виджету-окну библиотеки PyQt4. В данный класс из главного окна передается переменная «fd», содержащая полный путь до директории проекта задачи. Далее эта переменная передается в экземпляр служебного класса fd_class, путем вызова его функции post_fd (листинг 3). Кроме того, в классе листинга 2 осуществляется создание объекта класса Graphs_Data и вызов относящихся к нему функций (листинг 4). Представленный в листинге 4 программный код отвечает за формирование графика по скалярной величине Ux для параметра «Скорость» (U).
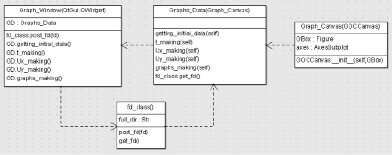
Рис. 1. UML-диаграмма модуля построения ГС
Листинг 3. Программный код служебного fd_class.py
class fd_class():
def post_fd(fd):
global full_dir
full_dir = fd
def get_fd(): return full_dir
В служебном классе fd_class заданы две функции, первая из которых отвечает за получение и сохранение переменной из внешнего модуля (главного окна), вторая – за передачу содержимого сохраненной переменной в другие модули графической оболочки.
Листинг 4. Graphs_Data.py
import re
import numpy as np
from add_classes.fd_class import fd_class
from add_classes.Graph_Canvas import Graph_Canvas
class Graphs_Data(Graph_Canvas):
def getting_initial_data(self):
global data, reg_prs
full_dir = fd_class.get_fd()
orf = open(full_dir+"/out_run.log", "r")
data = orf.read()
orf.close()
reg_prs = re.compile(r"(?<=[ ])\S*(?=[,])")
def t_making(self):
global t
t_reg = re.compile(r"Time\s=\s\S*\n")
t_mas = t_reg.findall(data)
fr_t_mas = []
fr_t = np.array([])
for g in range(len(t_mas)):
t_div = t_mas[g].split(" ")
fr_t_mas.append(t_div[2])
t = np.append(fr_t, fr_t_mas)
def Ux_making(self):
global Ux
Ux_reg = re.compile(r"\sUx,\sInitial\sresidual\s=\s\S*,\sFinal\sresidual\s=\s\S*")
Ux_mas = Ux_reg.findall(data)
fr_Ux_mas = []
fr_Ux = np.array([])
for g in range(len(Ux_mas)):
Ux_prs_mas = reg_prs.findall(Ux_mas[g])
fr_Ux_mas.append(Ux_prs_mas[2])
Ux = np.append(fr_Ux, fr_Ux_mas)
def graphs_making(self):
self.axes.plot(t, Ux)
self.axes.grid(True)
self.axes.set_xlabel("Time")
self.axes.set_ylabel("Koeff")
self.axes.set_yscale('log')
self.legend_lbls = ['Ux']
self.axes.legend(self.legend_lbls)
Функция getting_initial_data класса Graphs_Data (листинг 4) отвечает за создание переменной data, в которую помещается содержимое log-файла. В функции t-making посредством регулярных выражений осуществляется получение набора значений для параметра Time и, с помощью библиотеки NumPy, преобразование массива значений в допустимый для построения графических объектов формат.
Функция graphs_making отвечает непосредственно за построение ГС и указание их свойств. Команде «построить график» соответствует метод plot. В качестве аргументов этому методу передается ссылка на два аргумента (переменная или массив), содержащие значения, откладываемые по осям OX и OY системы координат.
Тестирование работы модуля
По итогам проведенной работы создано 4 компонента (файла) модуля: Graph_Canvas.py, Graph_Window.py, fd_class.py, Graphs_Data.py. Результат работы модуля после завершения процесса решения задачи, моделирующей эволюцию границы каверны при пуске торпеды, приведен на рис. 2 в главном окне графического интерфейса. Визуализация графика осуществляется в момент завершения процесса решения. Кроме того, предусмотрена возможность отображения графика при нажатии кнопки панели инструментов.
Представленный на рис. 2 график демонстрирует монотонную сходимость решения по параметру скорости (U), что свидетельствует о высокой точности решения и соответствии расчетных данных модели экспериментальным данным.
Заключение
В настоящей работе приведены особенности реализации модуля построения ГС для проектов задач МСС, моделируемых с помощью ПС OpenFOAM, и разработанного для него графического интерфейса. В статье представлена диаграмма взаимосвязи компонентов модуля, а также программный код каждого компонента. Настоящая статья может служить пособием для изучения связки инструментов Python 3.4, PyQt4, NumPy и Matplotlib, а также для проектирования модулей построения графиков.
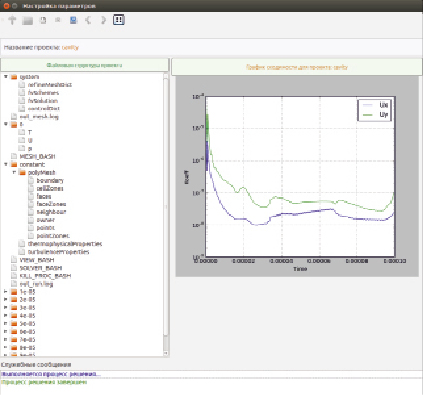
Рис. 2. Главное окно графического интерфейса с загруженным окном ГС
Библиографическая ссылка
Читалов Д.И., Калашников С.Т. ПОСТРОЕНИЕ ГРАФИКОВ СХОДИМОСТИ В ГРАФИЧЕСКОМ ПОЛЬЗОВАТЕЛЬСКОМ ИНТЕРФЕЙСЕ ПРОГРАММНОЙ СРЕДЫ OPENFOAM НА БАЗЕ БИБЛИОТЕК MATPLOTLIB И NUMPY // Современные наукоемкие технологии. 2017. № 11. С. 80-85;URL: https://top-technologies.ru/ru/article/view?id=36849 (дата обращения: 05.03.2026).
DOI: https://doi.org/10.17513/snt.36849



