Одна из актуальных задач, возникающих при построении автоматических систем управления подвижных объектов, – определение их навигационных параметров: линейных и угловых скоростей и ускорений, координат и углового положения. Одним из наиболее распространенных инструментов решения навигационной задачи являются бесплатформенные инерциальные навигационные системы (БИНС), интегрирующие вычисленные навигационные параметры с аналогичными параметрами других систем: одометрических, дальномерных и др.
В настоящее время наименее дорогими чувствительными элементами, в частности гироскопическими, для построения БИНС являются микромеханические датчики угловой скорости. В то же время дрейфы нуля и случайные угловые уходы для гироскопических каналов у данного типа датчиков приближаются к аналогичным параметрам вибрационных и волоконно-оптических датчиков. При этом на рынке широко представлены не полнофункциональные БИНС, а блоки инерциальных чувствительных элементов (БЧЭ), в результате чего задача реализации навигационных алгоритмов, их корректировка для конкретных типов БЧЭ и подвижных объектов возлагается на пользователя-разработчика.
Целью работы является разработка бесплатформенной инерциальной навигационной системы для решения задачи определения местоположения автоматизированной паллетной тележки в пределах складского помещения. Погрешность определения координат не должна превышать 3 % в автономном режиме, т.е. без использования показаний системы лидаров.
Квалифицированное и подробное описание алгоритмов начальной выставки в горизонт, навигации и интегрирования БИНС можно найти в работах [1–3], их развитие и модификации, а также опыт применения на подвижных объектах различного типа, в том числе наземных, – в работах [4–6].
Используемые блоки микромеханических инерциальных чувствительных элементов
Для решения поставленной задачи были выбраны блоки современных микромеханических инерциальных чувствительных элементов STIM300 (производство Норвегия) [7] и ADIS16488 (США) [8]. Данные блоки содержат триады гироскопических датчиков угловой скорости, акселерометров и инклинометров. Блоки чувствительных элементов выполнены по технологии MEMS.
STIM300 – это инерциальное измерительное устройство с высокой частотой измерений и низким энергопотреблением, которое не подпадает под экспортные ограничения в области высокотехнологичной продукции ITAR и на сегодняшний день имеет самые низкие дрейфы нуля и случайные угловые уходы для гироскопических и акселерометрических каналов среди микромеханических датчиков [7]. В табл. 1 приведено сравнение используемых блоков чувствительных элементов.
Проведение калибровки, разработка алгоритмов начальной выставки в горизонт и навигации, адаптация их для конкретного носителя, интегрирование с показаниями внешних по отношению к блокам чувствительных элементов измерительных устройств позволили реализовать на базе блоков чувствительных элементов полнофункциональные интегрированные бесплатформенные инерциальные навигационные системы.
Особенности подвижного объекта и маршрута его перемещения
В качестве подвижного объекта была выбрана автоматизированная паллетная тележка, функционирующая в многофункциональной системе, которая предназначена для автоматизации всех типовых напольных перемещений паллетных грузов на складе. Система состоит из электрической паллетной тележки, а также интеллектуальной системы автоматизации, которая обеспечивает возможность автономной работы без водителя.
Для вычисления координат и направления движения, а также для объезда препятствий используется система лидаров, представляющая собой излучатель, установленный на мобильной платформе, а также отражатели, закрепленные на стационарных вертикальных поверхностях помещения. Принцип работы аналогичной системы представлен в работе [9]. Погрешность вычисления координат системой лидаров составляет менее 1 % при условии достаточной видимости трех отражателей. Курсовой угол может быть вычислен с точностью до угловых минут. Отражатели для лидаров были установлены в испытательном ангаре так и в таком количестве, чтобы обеспечить высокоточное определение координат и курса тележки с высокой точностью на всем протяжении маршрута, поэтому измерения системы лидаров могли быть использованы в качестве образцовых сигналов. Для определения скорости движения используются энкодеры, установленные на колесах тележки.
Таблица 1
Основные параметры STIM300 и ADIS16488
|
Параметр |
Значение для STIM300 |
Значение для ADIS16488 |
|
Вес, г |
55 |
60 |
|
Габариты, мм |
45 × 39 × 22 |
47 × 44 × 14 |
|
Потребляемый ток, А |
0,3 |
0,4 |
|
Частота опроса, макс., Гц |
2000 |
2400 |
|
Гироскопические каналы |
||
|
Диапазон измерений, °/с |
400 |
450 |
|
Дрейф нуля (дисперсия Аллана), °/ч. |
0,5 |
5,1 |
|
Случайный угловой уход (дисперсия Аллана), °/vч. |
0,15 |
0,26 |
|
Нелинейность чувствительности, ppm |
± 25..50 |
± 35 |
|
Акселерометрические каналы |
||
|
Диапазон измерений, g |
10 |
18 |
|
Дрейф нуля (систематическая ошибка), mg |
0,05 |
0,45 |
|
Случайный угловой уход, м/с/vч. |
0,07 |
0,29 |
|
Нелинейность чувствительности, ppm |
± 100 |
± 280 |
|
|
|
|
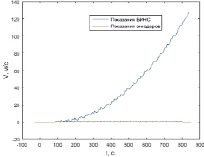
Рис. 1. График скорости, полученный в результате работы измененного базового алгоритма БИНС |
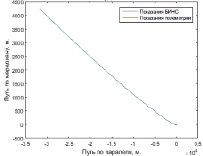
Рис. 2. График координат, полученный в результате работы измененного базового алгоритма БИНС |
|
|
|
|
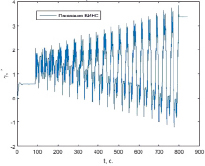
Рис. 3. График крена, полученный в результате работы измененного базового алгоритма БИНС |
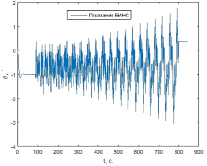
Рис. 4. График тангажа, полученный в результате работы измененного базового алгоритма БИНС |
|
|
|
|
Рис. 5. График курса, полученный в результате работы измененного базового алгоритма БИНС (на всем протяжении маршрута) |
Рис. 6. График курса, полученный в результате работы измененного базового алгоритма БИНС (на участке маршрута) |
При испытаниях на реальном складе были выявлены области протяженностью в десятки метров, на которых определение местоположения тележки оказалось либо невозможным, либо производилось с высокой погрешностью. В ходе испытаний были обнаружены ситуации, когда отражатели лидаров перекрываются различного рода объектами, такими как складская техника, грузы и т.п. Для решения этой проблемы было принято решение реализовать БИНС.
Реализованный алгоритм бесплатформенной инерциальной навигационной системы
Базовые принципы работы БИНС можно кратко изложить следующим образом. По результатам измерений гироскопических датчиков угловой скорости (ДУС), входящих в состав БЧЭ – блока микромеханических инерциальных чувствительных элементов (триады гироскопических ДУС и триады акселерометров) – производится аналитический расчет матрицы направляющих косинусов между связанной (с корпусом подвижного объекта) и навигационной системами координат (СК) [1]. В качестве навигационной используется полусвободная в азимуте СК. Первое интегрирование кажущихся ускорений в навигационной СК дает приращение линейной скорости движения, второе – приращение текущих координат. Для вычисления матрицы направляющих косинусов необходимо знать ее начальное значение, которое определяется по результатам начальной выставки в горизонт, проекции абсолютной угловой скорости связанной СК (измерения ДУС) и навигационной СК (рассчитываются с помощью результатов измерений акселерометров). Вычислительная схема базового алгоритма БИНС подробно изложена в работах [1, 10].
Для достижения поставленной цели в базовый алгоритм были внесены следующие изменения, обусловленные особенностями инерциального измерительного блока, подвижного объекта и испытательного маршрута.
1. Точность микромеханических ДУС недостаточна для счисления горизонтальной составляющей скорости вращения Земли, поэтому автономная начальная выставка по курсу не производится. Вместо этого один раз за весь маршрут осуществляется начальная выставка по заданному курсу – одномоментное совмещение истинного курса БИНС с курсом в системе координат ангара, определенным внешними датчиками – системой лидаров.
2. Средние значения выходных сигналов ДУС во время начальной выставки в горизонт принимаются в качестве статической погрешности измерения (предполагается, что это дрейф ДУС «от запуска к запуску»).
3. В качестве навигационной принимается не полусвободная в азимуте СК, а СК, непосредственно связанная с ангаром. Таким образом, приращение координат вычисляется как интеграл данных проекций при нулевых начальных условиях. Вычисление углов ориентации производится при условии, что угол азимута (угол свободы навигационной СК – ε) равен нулю.
4. Вычисление кватерниона учета «медленного» углового движения за счет вращения вместе с Землей и за счет движения вдоль поверхности Земли происходит только на этапе начальной выставки в горизонт.
Реализация алгоритмов бесплатформенной инерциальной навигационной системы
Изначально был реализован базовый алгоритм БИНС с вышеприведенными изменениями. Графики, построенные по результатам вычислений данного алгоритма, приведены на рис. 1–6.
Как можно увидеть из графика на рис. 1, абсолютное значение скорости состоит из полезной составляющей, отражающей истинное движение объекта, и нелинейно растущей погрешности, превышающей 120 м/с за 700 секунд функционирования БИНС. Такая погрешность вычисления скорости обусловлена значительным приведенным гироскопическим дрейфом, вызванным нестационарными погрешностями микромеханических инерциальных датчиков – нелинейностью масштабных факторов, неортогональностью установки и др. Маршрут изобилует участками разворотов по курсу, в результате проявляется взаимное перекрестное влияние измерительных каналов. Приведенный дрейф приводит к систематическому накоплению погрешностей вычисления углов крена и тангажа (рис. 3, 4), а это, в свою очередь – к непрерывному интегрированию на маршруте составляющих ускорения свободного падения. Корректное вычисление координат (рис. 2) при таких больших значениях погрешностей не представляется возможным.
Однако значения курса, изображенные на рис. 5, 6, являются удовлетворительными – за 700 секунд интенсивного маневрирования абсолютная погрешность не превысила 0.8 °.
Необходимость снижения погрешностей инерциальной системы требует применения алгоритмов самодемпфирования, однако на маршруте могут отсутствовать участки движения с постоянной скоростью. С другой стороны, хорошо идентифицируются интервалы полной остановки, которые складская автоматическая тележка совершает периодически в силу специфики своего применения. Также в качестве априорной информации можно считать заведомое отсутствие бокового движения (заноса) тележки.
Таким образом:
1) путевая (продольная) скорость движения объекта рассчитывается как
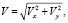 (1)
(1)
где Vx, Vy – составляющие скорости по осям x и y;
2) боковая (поперечная) скорость движения объекта полагается равной нулю;
3) составляющие скорости по осям x и y в СК, связанной с ангаром (N – навигационной), рассчитываются как
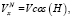 (2)
(2)
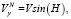 (3)
(3)
где H – курс инерциальной системы.
С учетом этой априорной информации в алгоритм функционирования БИНС были внесены изменения, в результате которых во время остановок производится выставка в горизонт с одновременным обнулением вычисленной БИНС оценки скорости. При этом коэффициенты демпфирования во время коротких остановок на маршруте необходимо выбирать существенно выше коэффициентов, которые используются при начальной выставке в горизонт, поскольку время начальной выставки в горизонт в отличие от времени остановки не ограничено.
В результате были реализованы два режима работы БИНС: автономный и демпфирования по скоростным измерениям энкодера. Автономный режим предполагает отсутствие корректировки показаний БИНС по результатам измерений внешних по отношению к БИНС измерительных устройств. Режим демпфирования по результатам скоростных измерений энкодера предполагает корректировку по результатам измерений энкодеров значений скорости перемещения по курсу.
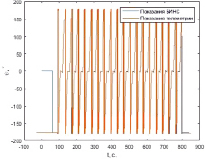
На рис. 7–8 представлены графики координат маршрута одного из заездов, построенные в результате проведения испытаний на складе. На рис. 7 представлен график координат, вычисленных в автономном режиме работы БИНС, на рис. 8 – график координат БИНС, демпфированной по скоростным измерениям энкодера. Прямая линия на этих графиках появилась в результате совмещения координат БИНС и системы лидаров в начальный момент времени.
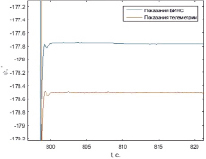
На рис. 9–10 представлены графики погрешностей вычисления координат демпфированной БИНС на базе STIM300 и ADIS16488 соответственно для трех заездов по одному маршруту.
Таким образом, удалось добиться снижения погрешности вычисления навигационных параметров по сравнению с автономным режимом работы БИНС. Погрешность вычисления координат в автономном режиме составила менее 2,6 %, в режиме демпфирования по результатам измерений энкодера – менее 0,2 %, что является достаточно низким значением для БИНС, построенной на микромеханических инерциальных чувствительных элементах низкого класса точности.
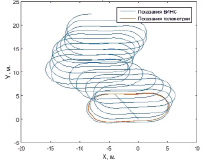
Рис. 7. Координаты в автономном режиме работы БИНС
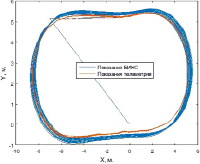
Рис. 8. Координаты БИНС, демпфированной по скоростным измерениям энкодера
<
Рис. 9. Погрешности вычисления координат демпфированной БИНС на базе STIM300
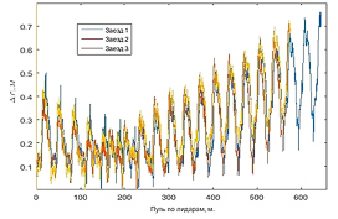
Рис. 10. Погрешности вычисления координат демпфированной БИНС на базе ADIS16488
Заключение
Разработанный навигационный алгоритм функционирования БИНС обладает следующими достоинствами, подтвержденными проведенными испытаниями:
1. Разработанный алгоритм проще базового алгоритма БИНС [1], что особенно важно для реализации его в реальном масштабе времени. Это связано с тем, что объект передвигается с малой скоростью по замкнутому маршруту небольшой площади, в качестве навигационной используется система координат, связанная с ангаром, поэтому нет необходимости учитывать эффекты переносного движения за счет вращения полусвободной в азимуте системы координат в инерциальном пространстве и т.д.
2. Повторяемость – результаты разных заездов практически повторяют друг друга. Алгоритмы для блоков чувствительных элементов разной точности (STIM300, ADIS16488) идентичны.
3. Небольшая погрешность определения координат объекта в автономном режиме – при общей протяженности маршрута 650 м и многократных разворотах по курсу (9 полных оборотов) абсолютная погрешность составила 17 метров.
4. Небольшая погрешность определения координат объекта в режиме демпфирования по скоростным измерениям – при аналогичных п. 3 параметрах маршрута абсолютная погрешность составила менее одного метра.
Библиографическая ссылка
Лукьянов В.В., Медведев В.О., Медведева Ю.Д. ОПРЕДЕЛЕНИЕ НАВИГАЦИОННЫХ ПАРАМЕТРОВ НАЗЕМНОГО ПОДВИЖНОГО ОБЪЕКТА С ПОМОЩЬЮ МИКРОМЕХАНИЧЕСКИХ ИНЕРЦИАЛЬНЫХ ДАТЧИКОВ // Современные наукоемкие технологии. 2017. № 11. С. 40-46;URL: https://top-technologies.ru/ru/article/view?id=36842 (дата обращения: 05.03.2026).