Движение условно монодисперсных твердых частиц мелких (d50 ≤ 100 мкм) и средних классов (100 мкм ≤ d50 ≤ 300 мкм) в горизонтальных и вертикальных трубопроводах исследовано в большом числе работ отечественных и иностранных авторов. Методы расчета таких течений, развиваемые авторами настоящей работы, базируются на подходе Лагранжа при описании движения твердых частиц, основываются на ряде упрощающих положений. В случае горизонтальных трубопроводов движение двухфазной среды представляется в виде суперпозиции горизонтальных плоских слоев, объемная доля частиц твердой фазы в которых постоянна в горизонтальном сечении и переменна в вертикальной диаметральной плоскости. Принимается также, что на частицы в продольном направлении действуют силы, определяемые произведением градиента давления на объем частицы, и гидравлического сопротивления. В вертикальном направлении на твердые частицы действуют силы: тяжести, Архимеда, Магнуса, Саффмана, знакопеременная сила турбофореза и гидравлического сопротивления. Также учитывается перенос частиц в вертикальном направлении за счет турбулентной диффузии. Таким образом, принимается, что твердые частицы одновременно перемещаются в горизонтальном и вертикальном направлениях. На основе приближенных расчетных моделей получены выражения для турбулентного трения и турбулентной диффузии при наличии в потоке твердых частиц. Следует подчеркнуть, что последние выражения не подбирались по результатам сопоставления опытных и расчетных данных по движению двухфазных потоков. В случае вертикальных трубопроводов, ввиду осевой симметрии двухфазного потока, объемная доля твердой фазы зависит от текущего радиуса расположения частицы. В соответствии с изменением ориентации трубы в вертикальном направлении вдоль потока действуют силы, определяемые градиентом давления, тяжести, Архимеда и сопротивления. В поперечном направлении действуют остальные силы и реализуется механизм диффузионного переноса твердых частиц.
Анализ предшествующих результатов
Как показано в работе [1], расчет по изложенной методике показал удовлетворительное соответствие с опытными данными по профилю объемной доли твердой фазы в диаметральном сечении трубопровода для частиц размером d50 = 90 мкм и d50 = 160 мкм при скорости перекачки от 3 м/с до 4, 44 м/с. Аналогичные результаты получены в работе [2] для частиц размером 165, 290 и 550 мкм при скорости перекачки от 3 м/с до 4,44 м/с.
Применительно к вертикальным трубопроводам было проведено сопоставление опытных и расчетных данных [3] для более крупных частиц с d50 = 470 мкм и d50 = 1700 мкм в трубопроводе с внутренним диаметром D = 40 мм при скорости перекачки 2,6 и 2,8 м/с. Предварительно проведенный теоретический анализ показал, что при движении сравнительно крупных твердых частиц, когда размер частицы примерно равен или превосходит величину линейного масштаба турбулентности, который определяется соотношением
λt = 0,015D, (1)
силу турбофореза не следует учитывать, так как она возникает из-за мелкомасштабных турбулентных пульсаций, которые не воздействуют на крупные частицы. Такое рассуждение подобно описанию эффекта броуновского движения мельчайших частиц, когда случайное столкновение с одной высокоскоростной молекулой жидкости изменяет положение частицы, а при росте размера частицы эффект броуновского движения исчезает в связи с увеличением размера частиц и резкого снижения эффективности взаимодействия с одиночной высокоскоростной молекулой жидкости. С учетом этого фактора результаты сопоставления в количественном и качественном отношении достаточно удовлетворительно согласуются с опытными данными, как по распределению объемной доли твердой фазы, так и по профилю скорости [3].
Цель работы
В настоящей работе анализируются опытные данные, полученные на двухфазных смесях с существенно большей крупностью твердых частиц. В связи с этим отметим, что, хотя соответствующие опытные данные опубликованы в течение последних пяти лет, авторам неизвестны результаты сопоставления этих и аналогичных опытных данных с альтернативными расчетными методами других авторов. Как нам представляется, это обстоятельство косвенно свидетельствует о необходимости дальнейшего совершенствования известных расчетных методов, что позволит уточнить области из применения. Целью настоящей работы является анализ движения частиц большой крупности в горизонтальных и вертикальных трубопроводах, что позволит уточнить используемую методику расчета и определить область её применения.
Анализ экспериментальных данных
В работе [4] приведены результаты экспериментальных исследований по движению стеклянных сферических частиц диаметром d = 6 мм плотностью 2540 кг/м3 и гравийных частиц с d50 = 6 мм при (4 мм ≤ d ≤ 8 мм), плотностью 2650 кг/м3 в горизонтальной трубе с внутренним диаметром D = 36 мм при скоростях движения гидросмесей от 1 м/с до 6 м/с и максимальной объемной доли твердой фазы 0,104. Используя формулу (1), получим d/λt = 11,1. Отметим также, что величина отношения D/d = 6. В этом случае, как отмечено в обзоре [1], представление о допустимости усреднения уравнений движения двухфазной среды является сомнительным.
В работе [5] приведены результаты экспериментальных исследований по движению базальтовых частиц с d50 = 11,0 мм плотностью 2787 кг/м3 в горизонтальных и наклонных трубах с внутренним диаметром D = 100 мм из гладкой нержавеющей стали при скоростях движения гидросмесей от 1,5 м/с до 5,5 м/с и максимальной объемной доли твердой фазы 0,14. В этом случае получим d/λt = 18,3 и D/d = 9,1.
В работах [6, 7] приведены результаты экспериментальных исследований по движению тех же базальтовых частиц в горизонтальной и вертикальной трубах с теми же характеристиками частиц и трубопровода и с несколько отличающимися объемными долями твердой фазы и скоростями перекачки. Естественно, что предыдущие оценки величин d/λt и D/d = 9,1 сохраняются.
Примечательным является то, что если в работе [4] приводятся некоторые эмпирические расчетные кривые, то в работах [6÷8] какое-либо прямое количественное сопоставление расчетных значений объемной доли твердых частиц в вертикальном диаметральном сечении трубы как в горизонтальных, так и вертикальных трубах с опытными данными отсутствует, а отмечается только их качественное соответствие.
Дальнейший анализ сосредоточим на опытных данных, приведенных в работах [5÷7], которые соответствуют большему значению величины d/λt = 18,3.
Уточнение методики расчета
При проведении численных расчетов с использованием методов, изложенных в работах [1÷3], наряду с замечанием о пренебрежении силой турбофореза, необходимо учесть и другие особенности связанные с размером и формой частиц.
Помещенные в работах [4÷7] фотографии базальтовых частиц показывают, что заостренные вершины и грани исходных частиц округлились, что можно было ожидать, за счет ударного взаимодействия между частицами и частицами со стенкой трубы, что, естественно, должно привести к уменьшению среднего размера частиц d50 с 11,7 мм до 11,0 мм. Из этих же фотографий следовало, что ни для первоначальных частиц, ни для окатанных частиц размер d50 не является параметром, характеризующим их гидродинамические характеристики, поскольку поперечные размеры частицы были примерно в два раза меньше. По форме частицы примерно соответствовали эллипсоидам вращения с отношением полуосей эллипсоида 2:1:1 при максимальном значении большой полуоси 5,5 мм и 2,75 мм – малой полуосью. В этом случае эффективный диаметр частицы, характеризующий её объем, равен dv = 6,93 мм.
Выполненный анализ формы частиц позволяет учесть её в используемом расчетном методе следующим образом. Принималось, что при движении частиц в продольном направлении вдоль стенки трубы частицы большой полуосью эллипсоида ориентированы параллельно стенке, с минимальным миделевым сечением, образованном малыми полуосями. При движении частиц в поперечном направлении, перпендикулярном к стенке трубы, поперечное сечение частицы определяется площадью эллипса, образованного малой и большой полуосями эллипсоида. Отсюда, в частности, следует, что при прочих равных условиях гидравлическое сопротивление в направлении стенки превосходит гидравлическое сопротивление частицы при её перемещении параллельно стенке. Такая ориентация частиц представляется естественной и соответствует самопроизвольной ориентации при движении удлиненных твердых тел в каналах (реках) и трубопроводах. В доступной авторам литературе такого уточнения в описании движения частиц ранее не производилось.
Экспериментальные данные представлены в виде зависимости удельных потерь напора от средней скорости гидросмеси Um. По этой причине для горизонтального и вертикального трубопроводов приведена одна «опорная» расчетная зависимость, а именно, потери напора в горизонтальном трубопроводе в трубе с гидравлически гладкой стенкой. В работе [8] отмечается, что приблизительно через 100–50 часов перекачки водопесчаных или водоугольных гидросмесей крупностью до 3 мм регулярная шероховатость всей внутренней поверхности трубы составляет примерно ks = 15–20 мкм. В работе [9] при определении трения двухфазного потока о стенку трубы предполагается, что результирующее трение складывается из трения частиц о стенку и трения жидкости о стенку, причем последняя считается шероховатой с величиной эквивалентной песочной шероховатости равной ks = 50 мкм. В этом случае, при R = 50 мм, отношение величины ks/R = 0,001, то есть относительно невелико. Заметим, что, например, в [8] средний размер частиц песка, хвостов и угля составлял 0,65; 0,5 и 2,0 мм при плотности 2600, 3400 и 1600 кг/м3 соответственно. В анализируемых опытах средний размер частицы в 5÷10 раз больше при достаточно большой плотности, и, следовательно, даже при уменьшении скорости столкновения частицы со стенкой, кинетическая энергия частицы, сталкивающейся со стенкой возрастает примерно пропорционально размеру частиц. Поэтому можно предполагать, что шероховатость поверхности может возрасти до ks = 200–500 мкм. Взаимодействие частиц абразивных материалов с поверхностью трубы, в первую очередь рассматривается как её механическая эрозия, то есть анализировалось уменьшение толщины стенки трубы, а возникновение и сохранение шероховатости её поверхности в процессе обработки практически не обсуждается [10, 11].
Следует также отметить, что шероховатость внутренней поверхности трубы определяется не в результате прямых измерений, а косвенным способом, путем измерения потерь давления при течении чистой жидкости и сопоставления её с теоретическим зависимостями. Так, например, в работе [12] получено, что для труб диаметром D = 155 мм, D = 204 мм и D = 305 мм при максимальной средней скорости движения Um = 8 м/с, Um = 5 м/с и Um = 3,5 м/с соответственно шероховатость стенки трубы двух первых труб составляет ks = 0 мкм, а третьей ks = 250 мкм. То есть в трубе максимального диаметра при наименьшей скорости потока, степень шероховатости стенки максимальна. Этот факт представляется несколько неожиданным, поскольку использовались частицы одного размера d50 = 0,54 мм и в одном диапазоне объемной доли частиц твердой фазы φ ≤ 0,22. Поскольку при такой крупности частиц локальная скорость движения частиц была одного порядка со скоростью жидкости, физически более вероятной казалась большая шероховатость поверхности трубы меньшего диаметра, поскольку скорость движения потока в этом случае была выше и, следовательно, локальные повреждения поверхности за счет ударного взаимодействия с поверхностью (локальные вырывы материала стенки) должны быть более значительными. В работе [12] оценка степени гидравлической гладкости стенки выполнялась с использованием формулы Блазиуса, правомерность применимости которой при числах Рейнольдса порядка 106 сомнительна. Проведенные нами оценки по формулам Прандтля для гладкой поверхности и Колбрука – Уайта для шероховатой поверхности показали, что действительно поверхности труб с диаметрами D = 155 мм и D = 204 мм могут характеризоваться как гидравлически гладкие с погрешностью в расчете скорости не более 7 %, а в трубе с D = 305 мм внутренняя поверхность характеризуется как шероховатая с эквивалентной шероховатостью ks = 250 мкм. В связи с последним значением шероховатости отметим, что в расчетах принималось, что труба по всей внутренней поверхности имеет одинаковую шероховатость. Физически ясно и опытные данные по абразивному износу внутренней поверхности горизонтальных труб показывают, что при перекачке абразивных гидросмесей износ вдоль нижней образующей трубы в кратность выше износа вдоль верхней образующей трубы. Поэтому можно предположить, что поскольку объемная доля частиц вдоль нижней образующей трубы в кратность (2÷10 раз) выше, чем вблизи верхней образующей трубы, то во столько же раз должны различаться и интервалы времени выхода на установившиеся значения шероховатости стенок на нижней и верхней образующих трубы. Поскольку тарировочные зависимости приводятся не всегда, степень шероховатости внутренней поверхности трубы является неопределенным параметром, влияющим на расхождение опытных и расчетных данных, особенно, в части расчета интегральных характеристик: средней скорости и удельных потерь напора.
Поскольку степень шероховатости поверхности трубы в работах [4÷7] определялась по тарировочным опытам для чистой воды, при проведении расчетов профиль скорости вблизи стенок рассчитывался по следующим зависимостям.
При расчете скорости вблизи гладкой стенки использовались модифицированные классические зависимости [13]
(2)
где U – локальное значение скорости, м/с; υτ – динамическая скорость, определяемая по трению на стенке, м/с; у – расстояние от стенки трубы, м; ν – кинематическая вязкость жидкости, м2 с; η = yυτ/ν – безразмерное расстояние от стенки.
В случае шероховатых поверхностей профиль скорости определяется выражениями, полученными в работе [14]:
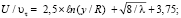
при ks ≤ y ≤ R, (3)
где R – внутренний радиус трубы, при осесимметричном течении, или расстояние от стенки до динамической оси потока, м; λ – коэффициент гидравлического сопротивления при произвольной степени шероховатости поверхности определяется выражением
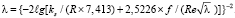, (4)
а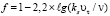 
– эмпирическая поправочная функция, зависящая от безразмерного комплекса (ksυτ/ν).
При небольших скоростях движения жидкости твердые частицы могут оседать на придонную поверхность вдоль нижней образующей трубы. В общем случае они могут образовать некоторое число n неподвижных слоев и m подвижных слоев. Предполагая, что частицы располагаются друг над другом, рассмотрим первый, касающийся поверхности трубы слой частиц. Условие, при котором первый слой частиц способен перемещаться, запишем в виде баланса силы, определяемой градиентом давления в жидкости, и суммы сил трения частицы о стенку и вышележащие слой частиц и гидродинамического сопротивления.
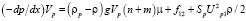, (5)
где (–dp/dx) – градиент давления в жидкости, Па/м; Vp – объем частицы, м3; ρp и ρ – плотность материала частиц и жидкости соответственно, кг/м3; μ – коэффициент механического трения частицы о стенку трубы; f12 – сила механического трения со стороны второго слоя частиц, если он перемещается, н; Sp – площадь миделевого сечения частицы в направлении движения потока, м2; Up1 – средняя скорость обтекания частиц первого слоя жидкостью, м/с.
В практическом плане воспользоваться такой зависимостью в расчетах для по существу полидисперсной смеси частиц (4 мм ≤ d ≤ 17 мм) при d50 = 11 мм, при не определенных в специальных опытах значений μ, f12 и сложности расчета величины Up1 практически невозможно, поскольку даже при благоприятных результатах сравнения опытных и расчетных данных это будет определяться удачным выбором неизвестных величин.
Для преодоления этой трудности примем дополнительную гипотезу, что в горизонтальных и вертикальных трубах скорость частицы, находящейся на расстоянии равном малой полуоси эллипсоида вращения, равна половине величины скорости на внешней стороне эллипсоида а расчетная объемная доля частиц равна объемной доле твердых частиц также на внешней стороне эллипсоида. В методологическом плане такой подход представляется логичным, поскольку каждая расчетная точка определяет положение центра частицы, которая не может приблизиться к стенке на расстояние меньшее полуширины малой оси эллипсоида вращения.
Сравнение экспериментальных и расчетных данных
Горизонтальная труба
При движении гидросмесей в горизонтальных трубах важнейшей характеристикой двухфазного потока является критическая скорость, которую рассчитаем по формуле [8]:
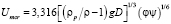, (6)
где Umcr – критическая скорость, м/с; φ – объемная доля твердой фазы; ψ – коэффициент фиктивного лобового сопротивления.
Для частиц с размером эффективного диаметра 5 мкм ≤ d ≤ 10 мкм ψ = 1,9. В анализируемых опытах d = 7 мм. В табл. 1 приведены значения критической скорости Umcr в зависимости от объемной доли твердой фазы φ.
Из данных, представленных в табл. 1, следует, что при скорости Umcr = 4,1 м/с устанавливается режим течения без возникновения слоя осадка на нижней образующей трубы.
На рис. 1 представлены экспериментальные значения распределения объемной концентрации твердой фазы в вертикальном диаметральном сечении трубы. Для двух значений объемной доли твердой фазы φ = 0,048 и φ = 0,134 нанесены расчетные зависимости.
В целом расхождение между опытными и расчетными зависимостями находится, как нам представляется, на достаточно удовлетворительном уровне. Наиболее значимое качественное различие имеет место в нижней, придонной части потока, в которой экспериментальное распределение концентрации твердой фазы имеет петлеобразный характер, причем эффект возрастает с ростом концентрации твердой фазы, а при φ = 0,048 практически не проявляется. В работах [6, 7] это объясняется тем, что имеет место сальтация частиц из нижнего придонного слоя частиц. Нам представляется, что такое объяснение нуждается в дополнительном пояснении. При установившемся движении потока причиной возникновения сальтации частиц является полидисперсность частиц твердой фазы и большие различия в форме частиц. В условиях рассматриваемых опытов, когда условный линейный размер частиц изменяется более чем в четыре раза, форма частиц изменяется от эллипсоидальной до почти сферической, также возрастает роль соударений между фактически не монодисперсными, а частицами разной формы и размера. Указанными факторами при расчетах условно монодисперсных потоков обычно пренебрегают. Необходимая для учета этих факторов информация практически отсутствует при описании опытных данных.
Таблица 1
Значения критической скорости в зависимости от объемной доли твердой фазы
|
φ |
0,034 |
0,048 |
0,074 |
0,082 |
0,124 |
0,134 |
|
Um cr, м/с |
2,53 |
268 |
2,88 |
2,94 |
3,14 |
3,18 |
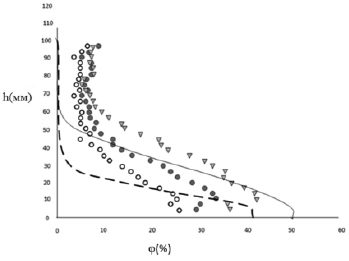
Рис. 1. Сравнение экспериментального и расчетного профиля концентрации твердой фазы φ в диаметральном сечении трубы при Umcr = 4,1 м/с. Опытные данные: 0 – φ = 0,048; • – φ = 0,082; ∇ – φ = 0,134. Расчетные зависимости: — φ = 0,133; – – – φ = 0,048
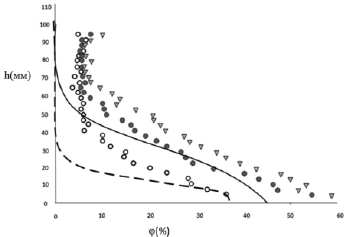
Рис. 2. Сравнение экспериментального и расчетного профиля концентрации твердой фазы φ в диаметральном сечении трубы при Umcr = 1,8 м/с. Опытные данные: 0 – φ = 0,034; • – φ = 0,074; ∇ – φ = 0,124. Расчетные зависимости: — φ = 0,133; – – – φ = 0,034
Примечательно, что для несколько отличающихся значений объемной концентрации φ и средней скорости Um = 2,8 м/с в работе [5] приведен подобный график, где этот эффект (горбообразное распределение) еще слегка заметен.
На рис. 2 представлены экспериментальные [5÷7] и расчетные значения объемной концентрации твердой фазы в вертикальном диаметральном сечении трубы для двух значений объемной доли твердой фазы φ = 0,048 и φ = 0,134 и скорости Um = 1,8 м/с.
В этом случае, поскольку Um < Umcr, должен реализоваться режим течения с возникновением слоя осадка твердых частиц на нижней образующей трубы. Опытное горбообразное распределение объемной концентрации твердой фазы не наблюдается. Расчетные значения концентрации частиц твердой фазы примерно так же согласуются с опытными данными, как и в предыдущем случае. Проведенное сопоставление опытных и расчетных данных показало, что, уточненная методика расчета позволяет рассчитать параметры гидросмеси для крупных частиц вплоть до относительных размеров d/λt = 18,3 и D/d = 9,1.
В табл. 2 приведены интегральные значения экспериментальных и расчетных величин, характеризующих рассмотренные опыты.
Из данных, приведенных в табл. 2, видно, что при перекачке со скоростью выше критической скорости соответствие между интегральными расчетными и опытными характеристиками двухфазного потока достаточно удовлетворительное и составляет около 5 %.
При движении со скоростью меньшей критической скорости расхождение в величинах градиента давления более существенно и достигает кратности. В связи с этим отметим, что данное обстоятельство имеет место и при использовании совершенно других методов расчета. Так, в работе [15] при обсчете 44 опытов между экспериментальными и расчетными величинами градиента давления составляло ± 20 % от среднего значения градиента давления при наличии отдельных отклонений, доходящих до 45 % от среднего значения, то есть тоже кратности. Такое значительного расхождение опытных и расчетных значений градиента давления, по-видимому, связано с упрощенными представлениями о движении частиц различной формы в потоке жидкости и взаимодействии частиц между собой и стенкой трубы и наличием слоя осаждения. Отметим также, что если вместо принятой в расчетах эллипсоидальной формы частиц, использовать эквивалентную по объему сферическую частицу, то расхождение между опытными и расчетными данными, как по интегральным характеристикам потока, так и по профилю объемной доли твердой фазы существенно возрастает.
Вертикальная труба
В случае вертикального трубопровода из общих потерь давления вычиталась величина избыточных гидростатических потерь давления, определяемых содержанием частиц твердой фазы Δp = (ρp – ρ)gh, где h – общая высота столба гидросмеси. То есть в качестве удельных потерь напора в вертикальном трубопроводе указывалась величина, определяемая именно наличием в потоке твердых частиц. При движении гидросмесей в вертикальных трубах предполагается, что имеется осесимметричное распределение частиц твердой фазы. К сожалению, в работах [4÷7] отсутствуют экспериментальные данные по распределению концентрации твердой фазы по радиусу. В работах [5÷7] приведены зависимости гидравлического уклона I от скорости перекачки двухфазных смесей при различных значениях объемной доли твердой фазы. Поскольку шероховатость поверхности в вертикальных трубах специальным образом не определялась, расчеты проводились в предположении, что поверхность гидравлически гладкая или имеет эквивалентную шероховатость ks = 20 мкм.
На рис. 3, 4 и 5 представлены результаты расчетов для трех значений объемной доли твердой фазы φ= 0,05, φ = 0,09 и φ = 0,14.
Анализ представленных данных показывает, что в целом в диапазоне указанных параметров имеет место достаточно удовлетворительное соответствие между опытными и расчетными значениями при скоростях перекачки от 1,5–2 м/с и выше. Расхождение опытных и расчетных данных заметно возрастает в области небольших скоростей, соответствующих небольшим значениям гидравлического уклона I. Отметим, что аналогичное положение имеет место и в случае горизонтальных труб.
Таблица 2
Сравнение интегральных характеристик двухфазных потоков в горизонтальной трубе
|
№ п/п |
Опыт |
Расчет |
||||
|
φ |
Um |
(–dp/dx) |
φ |
Um |
(–dp/dx) |
|
|
1 |
0,048 |
4,1 |
15451 |
0,0483 |
4,29 |
1500 |
|
2 |
0,134 |
4,1 |
23202 |
0,133 |
4,0 |
2200 |
|
3 |
0,034 |
1,8 |
5881 |
0,0338 |
1,89 |
400 |
|
4 |
0,124 |
1,8 |
12502 |
0,124 |
1,87 |
450 |
Примечание. 1 – соответствует φ = 0,05; 2 – соответствует φ = 0,14.
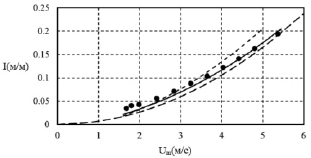
Рис. 3. Зависимость величины гидравлического уклона I от средней скорости Um при φ = 0,05. Опытные значения – •. Расчетные зависимости: — — — φ = 0 (чистая вода, стенка гладкая); — φ = 0,05 (двухфазный поток, стенка гладкая); - - - φ = 0,05 (двухфазный поток, стенка шероховатая ks = 20 мкм)
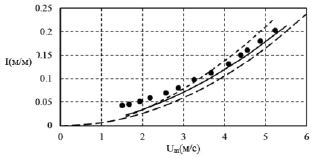
Рис. 4. Зависимость величины гидравлического уклона I от средней скорости Um при φ = 0,09. Опытные значения – •. Расчетные зависимости: – – – φ = 0 (чистая вода, стенка гладкая); — φ = 0,09 (двухфазный поток, стенка гладкая); - - - φ = 0,09 (двухфазный поток, стенка шероховатая ks = 20 мкм)
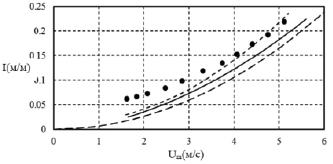
Рис. 5. Зависимость величины гидравлического уклона I от средней скорости Um при φ = 0,14. Опытные значения – •. Расчетные зависимости: – – – φ = 0 (чистая вода, стенка гладкая); — φ = 0,14 (двухфазный поток, стенка гладкая); - - - φ = 0,14 (двухфазный поток, стенка шероховатая ks = 20 мкм)
Заключение
Проведенный анализ позволил существенно уточнить используемый метод расчета, в части учета фактической формы твердых частиц при их движении в направлении движения потока вдоль трубы и при их перемещении в поперечном направлении, что приводит к различным значениям миделевого сечения перемещающейся твердой частицы в указанных направлениях, отличными от миделевого сечения эквивалентной сферической частицы. Показана возможность использования предложенного метода расчета для крупных твердых частиц, когда отношение характерных параметров потока достигает значений d/λt = 18,3 и D/d = 9,1.
При проведении дальнейших исследований представляется целесообразным уточнение методики расчета в части учета особенностей движении крупных частиц произвольной формы в потоке жидкости в части учета взаимодействия частиц между собой и стенкой трубы.
Библиографическая ссылка
Кондратьев А.С., Ньа Т.Л., Швыдько П.П. АНАЛИЗ ДВИЖЕНИЯ КРУПНЫХ ЧАСТИЦ В ГОРИЗОНТАЛЬНЫХ И ВЕРТИКАЛЬНЫХ ТРУБАХ // Современные наукоемкие технологии. – 2017. – № 11. – С. 31-39;URL: https://top-technologies.ru/ru/article/view?id=36841 (дата обращения: 21.11.2024).