В настоящее время разработаны и используются методы, реализующие различные виды логического вывода, в числе которых дедуктивный вывод (проверка выводимости заключения из базы знаний (БЗ)), абдуктивный вывод (пополнение БЗ фактами, необходимыми для вывода заключений), индуктивный вывод (добавление в БЗ общих правил) [1–4]. Одним из особых видов вывода является вывод логических следствий [5], позволяющий получать дедуктивные или абдуктивные (обеспечиваемые дополнительными фактами) следствия из новых фактов при заданном наборе исходных посылок.
Успешный логический вывод следствий часто сопровождается дополнительным результатом в виде схемы логического вывода, наглядно объясняющей пользователю порядок следования утверждений из исходных посылок. Схема вывода представляет собой ориентированный граф, вершины которого соответствуют секвенциям (посылкам), использованным при выводе, а дуги помечаются литералами этих секвенций. Описание такой схемы может быть сформировано в процессе логического вывода в виде множества литералов с параметрами. Например, по описанию O = {{A[15, 1], B[16, 1], M[17, 7], P[5, 7]}, {C[1, 3], D[2, 3], N[7, 11]}, {E[3, 4], V[11, 13]}, {L[4, 6]}, {R[6, 9], R[6, 10]}, {U[9, 12], S[8, 12], W[10, 13]}, {X[12, 14]}, {Y[13, +], Z[14, +]}} может быть построена схема логического вывода следствий, приведенная на рисунке.
Формальное описание схемы вывода следствий
Формальное описание схемы вывода зависит от вида вывода следствий и используемого исчисления (высказываний (ИВ) или предикатов (ИП)) для представления знаний. Все исходные секвенции нумеруются, образуя множество номеров секвенций N. Обозначим через A множество различных имен литералов, используемых в секвенциях. В ИП вершинам графа сопоставляются секвенции, модифицированные унифицирующими подстановками λ∈Λ, где Λ – множество унифицирующих подстановок, использованных в процессе логического вывода. При этом вершина графа помечается идентификатором λi j, состоящим из унифицирующей подстановки λi и номера модифицированной секвенции j∈N. Тогда описание схемы вывода можно представить в виде множества литералов для каждого варианта задачи:
1) дедуктивный вывод следствий:
а) SD = {L[j, k], L[j, +]} (ИВ);
б) S'D = {L[λij, ltk], L[λij, +]} (ИП);
2) вывод следствий при не полностью определенной БЗ:
а) SA = {L[j, k], L[j, +], L[+, k]} (ИВ);
б) S′A = {L[λi j, λtk], L[λi j, +], L[+, λtk]} (ИП).
Здесь j – номер секвенции, из вершины которой на схеме выходит, а k – номер секвенции, в вершину которой входит дуга, помеченная литералом L (L∈A, j, k∈N); «+» – символ вспомогательной переменной, определенной на множестве номеров секвенций N; L[j, +], L[λij, +] - конечные следствия; L[+, k], L[+, λtk] - дополнительные факты; λi, λt∈Λ. По номеру исходной секвенции однозначно определяются литералы, помечающие входящие и выходящие дуги вершины этой секвенции на схеме. В описании схемы используются только положительные (без инверсии) литералы, а пустые унифицирующие подстановки в идентификаторах вершин опускаются.
Ветвь на схеме логического вывода следствий
Основу ветви составляет последовательность литералов, которыми помечены дуги, соединяющие вершины схемы вывода. При этом правый номер каждого (за исключением последнего) литерала совпадает с левым номером следующего после него литерала, любой литерал может иметь дополнительные связи с другими литералами (не входящими в основу ветви), когда несколько литералов имеют одинаковые правые и различные левые номера. В общем случае ветвь можно представить в виде дерева, корнем которого является вершина с входящей дугой, помеченной последним литералом ветви.
Ветвление – это порождение двух и более ветвей, начинающихся с литералов, которые имеют одинаковые левые и различные правые номера (сами литералы могут быть одинаковыми). Две и более последовательности литералов, не имеющих друг с другом одинаковых номеров, представляют независимые ветви на схеме, которая делится на подсхемы, не имеющие общих вершин. Например, по приведенному выше описанию может быть сформировано две ветви: b1 = {M[17, 7], N[7, 11], P[5, 7], V[11, 13], Y[13, +], W[10, 13], R[6, 10], L[4, 6], E[3, 4], C[1, 3], D[2, 3], A[15, 1], B[16, 1]}, b2 = {A[15, 1], C[1, 3], B[16, 1], E[3, 4], D[2, 3], L[4, 6], R[6, 9], U[9, 12], X[12, 14], S[8, 12], Z[14, +]}.
Задача выделения ветвей
Из заданного нового набора фактов с помощью исходных посылок может выводиться не одно конечное следствие, причем некоторые конечные следствия могут выводиться не единственным образом. В таком случае схема логического вывода следствий содержит несколько ветвей, описывающих вывод. В связи с этим возникает задача выделения ветвей в схеме логического вывода следствий.
Задача может быть сформулирована следующим образом. Задано семейство множеств литералов, описывающих схему логического вывода следствий из множества новых фактов mF: O = {g1, …, gh, …, gH, s+}, где gh – множество литералов, полученное при формировании описания схемы на h-м шаге вывода; s+ - множество конечных следствий, из которых не выводятся новые следствия. Определить семейство множеств литералов B′ = {b1, …, bk, …, bK}, состоящее из множеств литералов bk, описывающих K ветвей логического вывода следствий.
Представление описания схемы в виде семейства множеств O позволяет упростить процесс выделения ветвей. Схема вывода следствий также может быть описана множеством литералов S = g1 ∪ … ∪ gH ∪ s+.
Процедуры формирования описаний ветвей
Процесс формирования описаний ветвей строится на основе следующих процедур: выбора предшествующих литералов; расширения ветви; выбора последующих литералов; удлинения ветви. Рассмотрим выделенные процедуры более подробно.
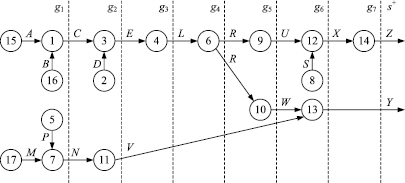
Схема логического вывода следствий: g1, …, g7 – множества литералов, полученные при формировании описания схемы вывода; s+ – множество конечных следствий, из которых не выводятся новые следствия
Процедура выбора предшествующих литералов. Процедура выбора предшествующих литералов имеет следующий вид: v = ⟨L, S, qv, mv⟩, где L - текущий литерал с параметрами; S - описание схемы вывода; qv - признак успешности процедуры («0» - нет предшествующих литералов, «1» - есть предшествующие литералы); mv - новое множество текущих литералов.
В процедуре выполняются следующие действия. Проверяется левый параметр текущего литерала, если он является символом вспомогательной переменной «+», то принимается mv = Ø, qv = 0. Иначе из множества литералов схемы вывода S выбираются и включаются во множество литералов mv литералы: а) L*[y, j] (для ИВ) такие, что правый параметр равен левому параметру текущего литерала L[j, x]; б) L*[y, λmj] (для ИП) такие, что λm ⊆ λi левого параметра текущего литерала L[λij, x] (здесь x, y - произвольные параметры, λi, λm - унифицирующие подстановки). В случае если таких литералов нет, то принимается mv = Ø, qv = 0, иначе qv = 1.
Процедура расширения ветви. Процедура расширения ветви имеет следующий вид:
w = ⟨mv, S, b*, b′⟩,
где mv = {L1, …, Lt, …, LT} - множество текущих литералов с параметрами; S - описание схемы вывода; b* - описание (множество литералов) расширяемой ветви; b′ – описание ветви после расширения.
Расширение ветви вывода представляет собой серию шагов, на каждом из которых параллельно выполняются процедуры выбора предшествующих литералов. Выбираемые этими процедурами литералы пополняют на каждом шаге формируемое описание ветви вывода. Процесс заканчивается, когда на очередном шаге все множества выбираемых литералов оказываются пустыми.
Введем следующие обозначения: h – номер шага по расширению ветви;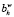 
– описание ветви, полученное на h-м шаге; 
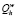– общий признак окончания расширения ветви («0» – процесс завершается, «1» – продолжается). Тогда описание процедуры с использованием индексной функции i(h) [6] может быть представлено в следующем виде.
1. Определение начальных значений:
h = 1,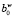 
= b*, i(1) = t, t = 1, …, T,
где T – число текущих литералов.
2. Выполнение процедур.
А) На первом шаге (h = 1) для каждого текущего литерала Lt выполняется процедура выбора предшествующих литералов:
,
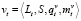где t = 1, …, T.
В результате формируются множества новых текущих литералов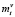 
для следующего шага и осуществляется переход к п. 3 (пункту 3).
Б) На втором и последующих шагах (h > 1) для множеств текущих литералов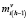 
, полученных в процедурах предыдущего шага (характеризуемых признаками 
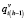= 1), выполняются следующие процедуры выбора предшествующих литералов:
,
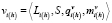где i(h) = i(h - 1).ti(h-1), ti(h-1) = 1, ..., Ti(h-1).
3. Формирование ветви. Производится пополнение описания ветви литералами, полученными в процедурах выбора литералов:
,
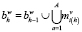где i(h) = i(h - 1).ti(h-1), a = ti(h-1), A = Ti(h-1).
4. Проверка общего признака окончания расширения ветви. Производится определение и проверка общего признака окончания расширения ветви.
,
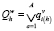где i(h) = i(h - 1).ti(h-1), a = ti(h-1), A = Ti(h-1).
Если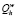 
= 1, то h = h + 1, выполняется п. 2.Б.
5. Фиксация результата выполнения процедуры: b′ =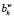 
.
Процедура выбора последующих литералов. Процедура выбора последующих литералов имеет вид:
u = ⟨L, S, qu, mu⟩,
где L - текущий литерал с параметрами; S - описание схемы вывода; qu - признак успешности процедуры («0» - нет последующих литералов, «1» - есть последующие литералы); mu - новое множество текущих литералов.
В процедуре выполняются следующие действия. Проверяется правый параметр текущего литерала, если он является символом вспомогательной переменной «+», то принимается mu = Ø, qu = 0. Иначе из множества литералов схемы вывода S выбираются и включаются во множество литералов mu литералы: а) L′[k, z] (для ИВ) такие, что левый параметр равен правому параметру текущего литерала L[x, k]; б) L′[λnk, z] (для ИП) такие, что λn ⊇ λt правого параметра текущего литерала L[x, λtk] (здесь x, z - произвольные параметры, λt, ln - унифицирующие подстановки). В случае если таких литералов нет, то принимается mu = Ø, qu = 0, иначе - qu = 1.
Процедура удлинения ветви. Процедура удлинения ветви имеет следующий вид:
U = ⟨L, b, S, p, N⟩,
где L - текущий литерал с параметрами; b - описание исходной ветви вывода; S - описание схемы вывода; p - признак успешности процедуры («0» - удлинение ветви невозможно, «1» - ветвь успешно продлена); N - множество, содержащее тройки «новый текущий литерал – описание соответствующей ему ветви – описание соответствующей ему схемы вывода» (при p = 1), или - «описание сформированной ветви» (при p = 0).
Процедура включает в себя расширение ветви и добавляет в описание ветви литерал, следующий после текущего. В общем случае вариантов удлинения ветви несколько, и они порождают множество новых ветвей. Описание процедуры может быть представлено в следующем виде.
1. Выполняется процедура v = ⟨L, S, qv, mv⟩. Если qv = 0, то принимается b′ = b и выполняется п. 3, иначе - b* = b ∪ mv.
2. Выполняется процедура w = ⟨mv, S, b*, b′⟩.
3. Выполняется процедура u = ⟨L, S, qu, mu⟩.
4. Производится установка признака p и фиксация множества N. Принимается p = qu. Если p = 1, то N = {⟨L1, b1, S1⟩, …, ⟨Lu, bu, Su⟩, …, ⟨LU, bU, SU⟩}, где Lu ∈ mu, bu = b′∪ {Lu}, Su = S - bu, иначе N = {b′}.
Рассмотренные процедуры позволяют построить метод формирования описаний ветвей.
Метод формирования описаний ветвей
Формирование описаний ветвей вывода представляет собой серию шагов, на каждом из которых параллельно выполняются процедуры U для каждого текущего литерала, соответствующих ему описаний исходной ветви и схемы вывода. Выбираемые этими процедурами литералы пополняют на каждом шаге формируемые описания ветвей вывода. При этом любая процедура U может породить несколько новых ветвей, для каждой из которых на следующем шаге будет выполняться своя процедура U. Процесс заканчивается, когда на очередном шаге все процедуры U завершаются неудачно (ни одна из ветвей не может быть продлена).
Введем следующие обозначения: h – номер шага по формированию ветвей; Bh – семейство множеств описаний ветвей, сформированных на h-м шаге; Ph – общий признак окончания формирования ветвей («0» – процесс завершается, «1» – продолжается). Тогда описание метода может быть представлено в следующем виде.
Из описания схемы логического вывода следствий, представленного семейством множеств O, выбирается множество литералов g1, полученное на первом шаге вывода. Из g1 выбираются литералы Lt[x, kt] (для ИВ), Lt[x, lkt] (для ИП) с различными правыми номерами параметров kt (здесь x - произвольный параметр, l - произвольная унифицирующая подстановка). Если g1 содержит несколько литералов с одинаковыми kt, то выбор одного из них может осуществляться по первому литералу с таким номером в порядке перечисления элементов множества.
1. Определение начальных значений:
h = 1, B0 = ∅, m = {L1, …, Lt, …, LT}, N = {⟨L1, b1, S1⟩, …, ⟨Lt, bt, St⟩, …, ⟨LT, bT, ST⟩}, bt = {Lt}, St = S - bt, i(1) = t, t = 1, …, T,
где T – исходное число текущих литералов.
2. Выполнение процедур удлинения ветвей. Для каждой тройки множества N или множеств Ni(h), полученных в процедурах предыдущего шага (характеризуемых признаками pi(h) = 1), выполняется процедура удлинения ветви:
Ui(h) = ⟨Li(h), bi(h), Si(h), pi(h), Ni(h)⟩,
где i(h) = i(h - 1).ti(h-1), ti(h-1) = 1, …, Ti(h-1).
3. Фиксация сформированных ветвей. Все описания сформированных ветвей b′i(h) добавляются в полученное на предыдущем шаге семейство множеств сформированных ветвей Bh-1. Если в Bh-1 уже имеется идентичное по содержанию описание ветви, то новое описание не добавляется. В результате семейство множеств Bh содержит только уникальные описания сформированных ветвей.
,
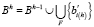где i(h) ∈ F, F – множество индексов признаков pi(h) = 0.
4. Проверка общего признака окончания формирования ветвей. Производится определение и проверка общего признака окончания формирования ветвей.
,
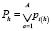где i(h) = i(h - 1).ti(h-1), a = ti(h-1), A = Ti(h-1).
Если Ph = 1, то h = h + 1, выполняется п. 2.
5. Фиксация результата выполнения метода. Выделенные в схеме вывода ветви фиксируются в семействе множеств описаний ветвей B′ = {b1, …, bk, …, bK}.
Применение метода подробно рассмотрено на примерах (ИВ, ИП) в работе [6].
Заключение
Предложенный метод решает задачу формирования описаний (выделения) ветвей из описания схемы вывода следствий, полученного с помощью методов дедуктивного вывода следствий и вывода следствий при не полностью определенной БЗ. При этом описание схемы вывода может быть представлено в исчислении высказываний или в исчислении предикатов. Метод отличается от известных использованием специальных процедур: выбора предшествующих литералов; расширения ветви; выбора последующих литералов; удлинения ветви. Метод обладает параллелизмом на уровне U процедур (удлинение каждой ветви) и v процедур (при расширении ветви), что позволяет более эффективно применять его при реализации интеллектуальных систем на современных параллельных вычислительных платформах.
Описания ветвей, сформированные в результате выполнения метода, могут быть использованы в качестве описаний траекторий в задаче логического прогнозирования развития ситуаций из заданной фазы.
Библиографическая ссылка
Симонов А.И., Страбыкин Д.А. ФОРМИРОВАНИЕ ОПИСАНИЙ ВЕТВЕЙ НА СХЕМЕ ЛОГИЧЕСКОГО ВЫВОДА СЛЕДСТВИЙ // Современные наукоемкие технологии. – 2017. – № 10. – С. 68-72;URL: https://top-technologies.ru/ru/article/view?id=36830 (дата обращения: 21.11.2024).