Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Иванов В.Н. 1 Шимановский В.А. 1

---

1 ФГБОУ ВО «Пермский государственный национальный исследовательский университет»

В работе представлена новая матричная форма уравнений движения механических систем, состоящих из абсолютно твердых тел и имеющих структуру дерева, выписанная относительно обобщенных координат, квазискоростей и обобщенных импульсов Пуассона. Предложены два алгоритма разрешения полученных уравнений относительно производных независимых координат, ориентированные на численное моделирование. Первый алгоритм является методом прогонки решения систем линейных алгебраических уравнений. Он аналогичен методу отдельных тел А.Ф. Верещагина, разработанного для разрешения уравнений движения цепочки тел относительно старших производных. Второй алгоритм основан на применении схемы Холецкого. Получены рекуррентные формулы, позволяющие алгоритмизировать все этапы формирования математической модели. Показано, что вычислительная трудоемкость решения уравнений динамики с использованием данных алгоритмов линейно зависит от числа тел в механической системе, что говорит об их эффективности. Выполнено сравнение алгоритмов между собой. Приведены результаты моделирования конкретных механических систем с большим числом степеней свободы, которые показывают преимущество алгоритма, основанного на схеме Холецкого перед методом прогонки.

Статья в формате PDF

0 KB

система абсолютно твердых тел

уравнения движения

динамика

математическое моделирование

обобщенные координаты

импульсы Пуассона

матрично-геометрический метод

разложение Холецкого

1. Классификация моделей систем твердых тел, используемых в численных расчетах динамического поведения машиностроительных конструкций / В.Н. Иванов [и др.] // Вестник Удмуртского университета. Математика. Механика. Компьютерные науки. – 2012. – № 2. – С. 139–155.

2. Компьютерные методы построения и исследования математических моделей динамики конструкций автомобилей / А.С. Горобцов, С.К. Карцов, А.Е. Плетнёв, Ю.А. Поляков. – М.: Машиностроение, 2011. – 463 с.

3. Погорелов Д.Ю. Алгоритмы моделирования динамики систем тел с большим числом степеней свободы // Вестник Нижегородского университета им. Н.И. Лобачевского. – 2011. – № 4–2. – С. 278–279.

4. Бойков В.Г., Юдаков А.А. Моделирование динамики систем твердых и упругих тел в программном комплексе EULER // Информационные технологии и вычислительные системы. – 2011. – № 1. – С. 42–52.

5. Иванов В.Н., Полосков И.Е., Шимановский В.А. Математические модели систем связанных твердых тел в импульсах Пуассона // Фундаментальные исследования. – 2016. – № 10–3. – С. 493–499.

6. Шимановский В.А. Метод компьютерного моделирования динамики систем связанных твердых тел // Фундаментальные исследования. – 2017. – № 8–1. – С. 104–109.

7. Верещагин A.Ф. Метод моделирования на ЦВМ динамики сложных механизмов роботов-манипуляторов // Изв. АН СССР. Техническая кибернетика. – 1974. – № 6. – С. 89–94.

8. Решение систем дифференциально-алгебраических уравнений последовательным исключением множителей Лагранжа / О.В. Шаповалов [и др.] // Известия Волгоградского государственного технического университета. – 2011. – Т. 10, № 3 (76). – С. 31–33.

9. Wittenburg J. Dynamics of multibody systems. – Berlin: Springer-Verlag, 2008. – 223 p.

10. Shabana A.A. Computational dynamics. – New York: Wiley, 2009. – 542 p.

11. Golub G.H., Van Loan C.F. Matrix Computations. – The Johns Hopkins University Press, 2012. – 790 p.

12. Hairer E., Norsett S.P., Wanner G. Solving ordinary differential equations I. Nonstiff Problems. – Springer-Verlag, 2011. – 528 p.

Компьютерное моделирование динамического поведения механических систем широко используется при проектировании новых изделий машиностроения. При этом в качестве расчетной схемы часто выступает система абсолютно твердых тел, шарнирно связанных друг с другом. Повышения точности компьютерного моделирования можно добиться за счет увеличения числа тел в системе. При этом увеличивается трудоемкость моделирования. Поэтому сохраняется потребность в совершенствовании методов, ускоряющих процесс математического моделирования [1–4].

В настоящей работе представлены алгоритмы формирования и разрешения уравнений движения систем твёрдых тел (СТТ), имеющих структуру дерева. Уравнения выписаны относительно расширенного множества переменных: обобщенных координат, обобщенных импульсов (переменных Гамильтона), квазискоростей и множителей Лагранжа. Статья является продолжением работ [5, 6]. В работе [5] из уравнений Эйлера – Лагранжа были выведены в явном матричном виде уравнения движения СТТ со структурой дерева в переменных Гамильтона (обобщенных координатах и импульсах), а в работе [6] были рассмотрены различные алгоритмы разрешения системы дифференциально-алгебраических уравнений движения СТТ в переменных Лагранжа (обобщенных координатах и скоростях) относительно групп независимых переменных. В настоящем исследовании численные алгоритмы, разработанные в работе [6], адаптируются к уравнениям движения в переменных Гамильтона. Выполнено сравнение алгоритмов по их вычислительной эффективности.

Описание механической системы

Рассмотрим СТТ со структурой дерева. Будем считать, что связи в шарнирах являются голономными и идеальными.

Пусть число тел и шарниров в системе равно N. При этом в качестве первого шарнира выбирается шарнир между одним из тел системы и «нулевым» телом. Будем считать, что закон движения «нулевого» тела в абсолютной системе координат Oxyz задан.

Введем нумерацию тел так, чтобы номер тела, являющегося носителем i-го тела 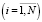в графе системы был меньше i. В этом случае шарнир между i-м телом и его носителем будет иметь номер i. Тогда структуру взаимосвязей в механической системе можно описать одним целочисленным массивом 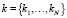, i-м элементом которого является номер тела, предшествующего i-му. Введем в рассмотрение следующие множества: Pi – упорядоченные множества номеров шарниров, входящих в пути между нулевым и i-ми телами; Ki – множества номеров тел, являющихся дочерними для каждого i-го тела.

Положение и ориентацию i-го тела в пространстве будем задавать с помощью радиуса-вектора 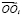некоторой точки Oi тела и трех ортонормированных векторов 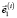, , 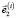, 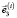определяющих базис связанной с i-м телом системы координат (СК) .

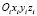Введем обозначения: ri = OOi – матрица-столбец координат вектора 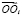; 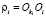– матрица-столбец координат вектора 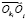в СК ki-го тела; 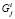– матрица преобразования координат из СК, связанной с j-м телом, в СК i-го тела (матрица направляющих косинусов).

Предположим, что в i-м шарнире на систему накладывается l_i ≤ 6 интегрируемых, линейно-независимых связей. В этом случае множество возможных относительных положений i-го тела будет являться ni-мерным конфигурационным многообразием [5], где ni = 6 – l_i. Введем матрицу-столбец 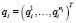обобщенных координат (параметров), определяющих положение любой точки этого многообразия. Тогда матрицы ρ_i и 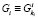, задающие относительное положение i-го тела, будут являться функциями этих параметров:

, .

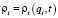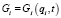Параметризация возможных перемещений в каждом шарнире позволяет однозначно определить положение всех тел системы в абсолютной СК в любой момент времени t с помощью следующих рекуррентных формул:

, .

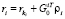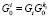Тогда проекции линейной скорости vi и угловой скорости ω_i i-го тела механической системы на оси СК, связанной с i-м телом, можно вычислить по следующим рекуррентным формулам:

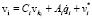, (1)

где

, , ,

, ,

, ,

, .

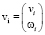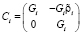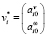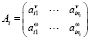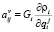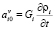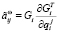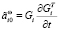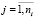Символом «~» обозначены кососимметричные матрицы векторного произведения.

Введём в рассмотрение матрицу :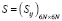

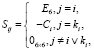
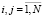. (2)

Заметим, что для любой кинематической структуры механической системы в каждой строке этой блочной матрицы содержится только два блока E6 и –Ci, не являющихся нулевыми. Матрица S содержит информацию о структуре системы и об относительных положениях всех тел. Используя матрицу S, кинематические уравнения (1) можно записать следующим образом:

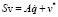, (3)

где

,

, .

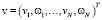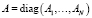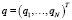Формулы (3) так же можно представить в явном виде

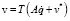, (4)

где блоки обратной к S матрице T = S–1 можно вычислить по формулам

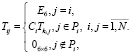(5)

Уравнения движения в импульсах Пуассона

Введем следующие обозначения:

, ,

,

, ,

, ,

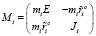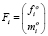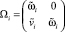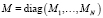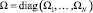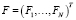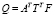где mi, Ji – массы и тензоры инерции тел системы; 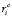– матрицы-столбцы проекций радиус-векторов центров масс тел на оси связанных с ними СК; 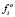, 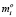– проекции главных векторов и моментов активных сил в СК тел системы; Q – матрица-столбец обобщенных сил.

Тогда уравнения движения СТТ, имеющих структуру дерева, можно записать относительно расширенного множества переменных в виде

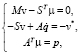(6)

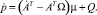(7)

Уравнения (6), (7) образуют замкнутую систему уравнений относительно квазискоростей v, обобщенных скоростей 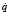, переменных μ (множителей Лагранжа) и производных 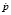от обобщённых импульсов Пуассона. При этом уравнения (7) разрешены относительно импульсов Пуассона, а три уравнения (6) являются системой линейных алгебраических уравнений с блочной, трёхдиагональной, симметричной, разреженной матрицей. Полный вывод уравнений движения СТТ (6), (7) можно найти в работе [5].

Заметим, что уравнения (6) по форме аналогичны системе уравнений движения СТТ, описанной в работах [1, 6]:

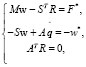(8)

где w – матрица-столбец проекций абсолютных декартовых ускорений (линейных и угловых) всех тел системы на оси СК, связанных с ними. Члены F* и w* в правых частях уравнений содержат внешние активные силы и все силы, порождаемые гироскопическими, центробежными, кориолисовыми и явно зависящими от времени ускорениями.

В отличие от уравнений (8), которые служат для определения обобщенных ускорений 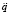, уравнения (6) используются для вычисления обобщенных скоростей .

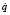Однако по структуре уравнения (6) и (8) совпадают. Это позволяет применить для системы уравнений (6) алгоритмы, разработанные ранее для решения системы уравнений (8). Например, метод отдельных тел А.Ф. Верещагина [7], методы редукции к уравнениям движения в форме Лагранжа 2 или 1 рода [8–10].

Преимущество формы уравнений (6), (7) состоит в том, что при наличии дополнительных геометрических или кинематических связей в механической системе уравнения (6), (7) могут быть замкнуты только уравнениями кинематических связей, а не продифференцированными дважды уравнениями связей, как в случае использования уравнений (8). При этом методы стабилизации связей (типа метода Баумгарта [9]), применяемые для уравнений (6), (7), обеспечивают экспоненциальный закон компенсации отклонений в случае нарушения связей и не приводят к появлению дополнительных «паразитных» малых высокочастотных колебаний в механической системе. Это означает, что при применении известных численных методов интегрирования дифференциально-алгебраических уравнений к уравнениям движения вида (6), (7) возможен больший шаг интегрирования, следовательно, меньшее время компьютерного моделирования.

В работе [6] получены алгоритмы метода прогонки и Холецкого разрешения системы уравнений (8) относительно старших производных. В настоящей статье аналогичные алгоритмы построены для уравнений (6), (7) в импульсах Пуассона.

Решение уравнений движения в импульсах Пуассона методом прогонки

Уравнения (6) являются системой линейных алгебраических уравнений (СЛАУ) относительно обобщенных скоростей, квазискоростей, множителей Лагранжа и имеют ленточную структуру. Поэтому для их разрешения относительно этих групп переменных можно выписать метод прогонки как модификацию метода Гаусса решения СЛАУ. На прямом ходе данного метода выполняется последовательное исключение множителей Лагранжа μ, начиная с концевых тел СТТ. На обратном ходе последовательно вычисляются обобщённые скорости 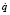, декартовые скорости v и множители Лагранжа μ для каждого тела системы, начиная с первого.

Вывод рекуррентных формул метода прогонки подробно изложен в статье [5]. Здесь же приведём только результирующий алгоритм метода.

Алгоритм метода прогонки

for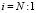

,

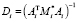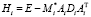
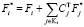
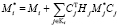
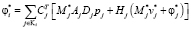
end

for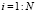

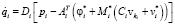
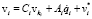
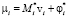
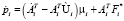
end

Число арифметических операций, которые необходимо выполнить в данном алгоритме для разрешения системы уравнений (6), (7), растёт линейно в зависимости от числа тел в СТТ. В этом алгоритме происходит обращение небольших положительно определённых симметричных матриц 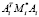, порядок которых равен числу обобщенных координат в i-м шарнире. Поэтому этот метод оказывается эффективным для численного моделирования СТТ с длинными кинематическими цепями.

Разрешение уравнений движения с использованием факторизации Холецкого

Метод прогонки в матричном виде реализует LU-разложение [11] матрицы системы уравнений (6) и не использует все свойства этой матрицы. Заметим, что она симметрична, блочно трехдиагональна, но не является положительно определенной. Поэтому для разрешения системы уравнений (6) можно применить LTDL-разложение Холецкого [11], модифицируя его на случай неопределенности матрицы системы. Заметим, что при LTDL-разложении разреженных систем линейных уравнений, имеющих ленточную структуру, треугольные множители L остаются ленточными матрицами.

Введем обозначения:

,

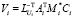где 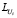– факторы Холецкого положительно определенных симметричных матриц 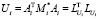. Тогда .

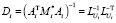Подставляя выписанные разложения в формулы алгоритма метода прогонки, можно после несложных преобразований получить следующий алгоритм разрешения системы уравнений (6), (7).

Алгоритм метода Холецкого

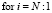
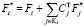
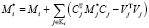
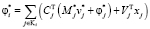
Найти фактор Холецкого 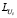матрицы

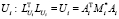
Решить 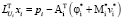относительно xi

Решить 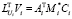относительно Vi

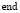
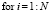
Решить 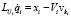относительно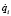

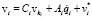
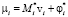
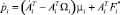
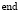
В данном алгоритме, как и в предыдущем, число арифметических операций связано линейной зависимостью с числом тел в СТТ. Но вместо вычисления обратных матриц 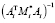находятся их факторы Холецкого и решаются системы линейных уравнений с треугольными матрицами. Поэтому вычислительная эффективность разрешения уравнений движения (6), (7) полученным алгоритмом оказывается выше, чем методом прогонки. Полный вывод аналогичных формул для системы уравнений (8), использующий LTDL-разложение матрицы системы и факторизацию Холецкого для блоков этой матрицы, приведен в работе [6].

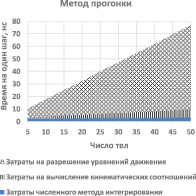
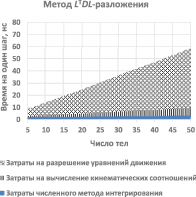
а) б)

Рис. 1. Зависимость времени, затраченного на выполнение одного шага интегрирования, от числа тел в механической системе для двух рассмотренных методов разрешения уравнений движения

Результаты численных экспериментов по сравнению эффективности методов

Перед тем как приводить результаты численных экспериментов по сравнению рассмотренных выше методов разрешения системы уравнений (6), (7), заметим, что теоретические оценки показывают [11], что в методе Холецкого, учитывающего симметрию матрицы системы, число арифметических операций в два раза меньше, чем в методе прогонки. Однако практические результаты сравнения эффективности методов отличаются от теоретических.

Например, при численном моделировании динамики СТТ кроме временных затрат на разрешение уравнений (6) относительно обобщенных скоростей существуют общие затраты, связанные с вычислением кинематических характеристик и сил, действующих на механическую систему, а также затраты самого метода интегрирования дифференциальных уравнений (6), (7) после их разрешения.

Описанные выше алгоритмы применялись для численного моделирования динамики СТТ, представляющих собой цепочки тел, соединённых двухстепенными кардановыми шарнирами. Дифференциальные уравнения интегрировались методом Штёрмера [12] шестого порядка. Сравнивалось время выполнения одного шага. При этом варьировалось число тел в системе.

На рис. 1 для двух рассмотренных алгоритмов разрешения уравнений (6), (7) приведены графики зависимостей затрат времени на выполнение одного шага интегрирования от количества тел в системе.

Графики подтверждают теоретические выводы о том, что время, затрачиваемое на численное моделирование, линейно зависит от числа тел в системе. Причём, львиную долю составляют затраты времени на разрешение уравнений движения.

Для сравнения эффективности рассмотренных методов приведем график отношения временных затрат T1/T2 на разрешение уравнений движения (рис. 2), где T1 и T2 – время, затрачиваемое на разрешение уравнений методом прогонки и методом LTDL-разложения соответственно.

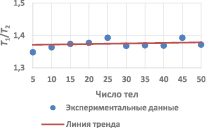
Рис. 2. График отношения T1/T2

Из приведенного графика видно, что метод, использующий факторизацию Холецкого и учитывающий симметричность матрицы системы уравнений движения (6), (7), эффективнее метода прогонки. Рис. 2 показывает, что алгоритм LTDL-разложения позволяет в 1,35–1,4 раза сократить время, затрачиваемое на разрешение уравнений движения по сравнению с методом прогонки.

Заключение

В статье приведена новая компактная матричная форма записи уравнений движения СТТ, имеющих структуру дерева, выписанная относительно обобщенных координат, квазискоростей и обобщенных импульсов Пуассона.

Предложены два рекуррентных алгоритма разрешения этих дифференциальных уравнений относительно старших производных: метод прогонки и метод, использующий LTDL-разложение и факторизацию Холецкого. Выполнено сравнение алгоритмов по их вычислительной эффективности. Приведенные примеры моделирования СТТ с различным числом тел показывают, что алгоритм, использующий факторизацию Холецкого, позволяет ускорить расчеты по сравнению с методом прогонки на 35–40 %.

Библиографическая ссылка