Рациональное использование природных богатств является одной из важнейших задач XXI века. К одному из путей решений данной задачи относится очистка различных технических жидкостей от посторонних примесей [1]. Особое место среди всех типов технических жидкостей занимают смазочно-охлаждающие жидкости (СОЖ), предназначенные в основном для смазки и охлаждения металлообрабатывающих инструментов, деталей и трущихся частей механизмов, что способствует снижению износа инструментов, повышению точности обработанных деталей и надежности работы механизмов [2]. Средний срок использования СОЖ составляет от двух недель до нескольких месяцев. Главными причинами их замены являются превышение предельно допустимой концентрации механических посторонних примесей (металлическая пыль, сажа, частицы абразивных материалов), расслаивание и загнивание.
На сегодняшний день существует только четыре базовые механизма извлечения примесей из жидкостей или газов механического способа: под действием сил гравитации (осадители, отстойники); инерции (циклоны, гидроциклоны, скрубберы, центрифуги); ситовый эффект (фильтры) и сепарация под действием внешнего воздействия (сепараторы, классификаторы) [3, 4]. В связи с тем, что СОЖ применяются в основном при работе с металлическими предметами, частицы, загрязняющие эти самые жидкости, часто являются ферромагнитными. Таким образом целесообразно применять магнитное поле для интенсификации процесса их извлечения. Более подробно воздействие магнитного поля на процесс извлечения представлено в [5, 6].
Одним из самых перспективных способов использования магнитного поля для повышения эффективности извлечения ферромагнитных частиц является магнитный гидроциклон. В данной статье будет рассматриваться гидроциклон с радиальным магнитным полем, как аппарат с наиболее простой и эффективной конструкцией.
Целью работы является создание математической модели кинетики частиц в рабочей камере магнитного гидроциклона.
Коагуляция – объединение мелких частиц в более крупные под воздействием сил сцепления. Этот процесс играет важную роль в металлургии, аппаратах химической промышленности, горно-обогатительном комплексе и т.д.
Процесс коагуляции схематически изображен на рис. 1.
В [7] приведена модель коагуляции двух частиц в криволинейном потоке, однако и она требует дальнейшего совершенствования.
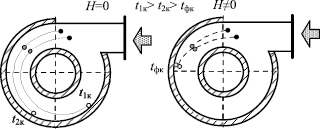
Рис. 1. Процесс извлечения дисперсной среды в гидроциклоне без наложения магнитного поля (а) и с наложенным магнитным полем (б); H – напряженность поля; t1к, t2к, tфк – время достижения внешней стенки гидроциклона первой частицей, второй и образовавшейся флокулы соответственно
Рассмотрим движение твердой или жидкой частицы в жидкости, начиная с общего обсуждения и фокусируясь на движении частиц в закрученном потоке.
В гидроциклоне частицы почти всегда движутся относительно потока с их конечной скоростью, а конечная скорость данной частицы определяет, будет ли она захвачена или потеряна. Эта предельная скорость в точности аналогична скорости оседания частицы в гравитационном поле Земли в стационарных условиях, за исключением того, что для аппаратов инерциального типа радиально направленная центробежная сила заменяет гравитационную.
Для вычисления конечной скорости частицы в вихревом потоке начнем с уравнения движения частицы. Применяя закон Ньютона к частице, движущейся в жидкости, приравняв произведение ускорение на массу к сумме действующих на нее сил Fi, получим
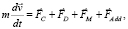 (1)
(1)
где m – масса частицы, кг; v – скорость частицы, м/с; FC – центробежная сила, Н; FD – сила сопротивления среды, Н; FM – магнитная сила, Н; FAdd – дополнительные силы, влияние которых значительно меньше, чем перечисленных выше. К дополнительным силам можно отнести гравитационную, архимедову, подъемную силу (эффект Магнуса), силу Саффмана, силу, создаваемую дополнительной массой, и силу Бассета. Более подробно анализ сил, действующих на частицу приведен в [7].
Магнитная сила вычисляется по формуле:
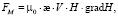 (2)
(2)
где Н и gradH – напряженность поля (А/м) и его градиент соответственно; μ0 = 4π•10-7, æ и V – магнитная восприимчивость и объем (м3) частицы соответственно.
Так как магнитная сила велика только у выходного патрубка, а в большей части рабочей камеры она близка к нулю (gradH ≈ 0), то для дальнейших расчетов магнитную силу будем опускать. При соответствующей подстановке в выражение (1) общее уравнение движения частицы в ньютоновской жидкости становится:
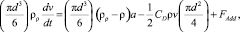 (3)
(3)
где а – вектор ускорения внешнего силового поля; ρ и ρ – плотность частиц и жидкости соответственно, кг/м3; CD – коэффициент сопротивления.
FAdd относится к быстрому нестационарному движению. Добавленный массовый член учитывает тот факт, что при ускорении частицы из покоя окружающая жидкость также должна быть ускорена. Сила Бассета показывает, что за счет быстрого изменения движения сопротивление будет зависеть не только от его мгновенной скорости относительно жидкости, но и от предыдущего движения, поскольку картина течения жидкости может не успевать регулироваться из-за инерции жидкости. Эти два члена равны нулю при устойчивом движении.
Сила сопротивления среды определяется по формуле:
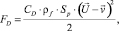 (4)
(4)
где Sp – поперечное сечение частицы, м2; U – скорость потока вязкой среды, м/с.
При малых значениях числа Рейнольдса можно воспользоваться более простой формулой – приближенным законом Стокса для шарообразных частиц [8]:
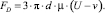 (5)
(5)
Эти упрощения дают следующее уравнение движения частицы:
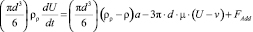 . (6)
. (6)
Решаем дифференциальное уравнение (6) в одном направлении, считая U(0) = U0, относительная скорость частицы к потоку примет следующий вид:
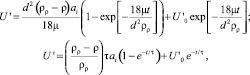 (7)
(7)
где τ называется «временем релаксации частицы», с [9]:
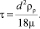 (8)
(8)
При больших t экспоненциальные члены обращаются в нуль, а частица достигает конечной скорости. Конечная скорость вычисляется:
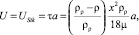 (9)
(9)
где UStk – скорость Стокса, то есть конечная скорость частицы при применении закона Стокса [10]. Небольшие частицы быстро достигают конечной скорости. Это следует из уравнения (9): τ мало при малых d, поэтому экспоненциальный член быстро стремится к нулю. Исходя из вышесказанного можно пренебречь нестационарной частью уравнения (9) даже для быстрых, мелкомасштабных флуктуаций скорости, вызванных турбулентностью, и предположить, что частица всегда будет находиться на конечной скорости относительно несущего потока.
На рис. 2 представлена зависимость скорости частицы от времени. Частица приближается к своей конечной скорости в течение нескольких микросекунд. Как уже упоминалось, закон Стокса для лобового сопротивления справедлив для малых чисел Рейнольдса. Другое требование применения закона Стокса состоит в том, что окружающая жидкость может рассматриваться как сплошная среда. Это условие не соблюдается для очень маленьких частиц (в субмикронных размерах) или в циклонах, работающих в условиях высокого вакуума. Здесь необходимо принять во внимание тот факт, что газ состоит из отдельных молекул. Это имеет два эффекта:
1. Столкновения с молекулами потока вызывают колебательное движение частиц (броуновское движение). Этим можно пренебречь по сравнению с любой крупномасштабной дисперсией турбулентных частиц.
2. Между потоком несущей среды и частицей происходит скольжение, поскольку свободное пространство между молекулами становится сравнимым с размером частиц. Это учтено поправочным коэффициентом Каннингема:
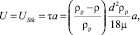 (10)
(10)
где λ – длина свободного пробега молекул.
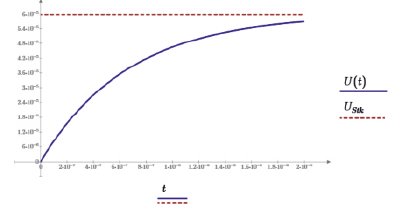
Рис. 2. Скорость частицы в вязкой среде (d = 10 мкм, ρp = 7800 кг/м3, ρ = 800 кг/м3, a = 100 м/с2, μ = 65 мПа•с)
Обратим теперь внимание на поведение частицы в закрученном потоке. Сила, возникающая из-за градиента давления в жидкости, которая в этом контексте сродни архимедовой силе, действующей в гравитационном поле, не будет удерживать частицу на своем пути, если она не будет иметь ту же плотность, что и жидкость. В инерционных аппаратах плотность частиц значительно выше плотности среды, поэтому «плавучесть» мала и частица будет двигаться радиально наружу в вихре. В отдельных случаях можно даже игнорировать плавучесть при вычислении скорости частицы, так что единственной значительной силой, противостоящей наружному радиальному движению частицы, является сила сопротивления. Центробежная сила для современных циклонов и гидроциклонов в несколько десятков или сотен раз может превышать гравитационную.
Для того чтобы оценить тангенциальную скорость жидкости, воспользуемся формулой Дриссена [11]:
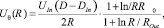 (11)
(11)
где UIn – входная скорость жидкости, м/с; DIn – диаметр входного патрубка, м; R0 – диаметр выходного патрубка, м; ROut – диаметр сливного патрубка, м.
В случае, когда входной патрубок МГЦ в сечении имеет форму прямоугольника, эквивалентный диаметр высчитывается по следующей формуле:
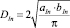 , (12)
, (12)
где aIn и bIn – соответственно высота и ширина входного патрубка прямоугольного сечения.
Подставив значения тангенциальной скорости потока (9) в систему уравнений коагуляции частиц, представленной в [7], получим следующую математическую модель:
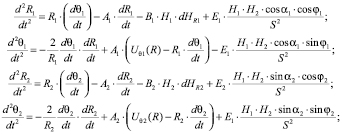 (13)
(13)
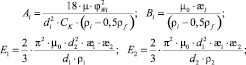
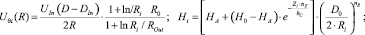
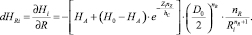
Система уравнений (13) решалась численным методом с помощью САПР MathCAD при следующих условиях (рис. 3): d1 = 70 мкм; d2 = 90 мкм; частицы – железный порошок, среда – вода; H0 = 4·104 А/м. Начальные условия: R10 = 0,037 м; R20 = 0,03 м; θ10 = 1,75 рад; θ10 = 1,6 рад; vR10 = vR20 = 0 м/с; vθ10 = vθ20 = 2 м/с.
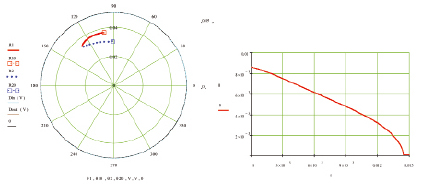
а) б)
Рис. 3. Результаты численного исследования математической модели процесса коагуляции двух частиц в рабочей камере гидроциклона (а) и зависимость расстояния от времени между двумя коагулирующими частицами (б)
Полученная модель является более точной иллюстрацией кинетики коагуляции ферромагнитных частиц в рабочей камере гидроциклона под действием магнитного поля.
Выводы
Разработана уточненная математическая модель взаимодействия двух частиц в рабочей камере гидроциклона под действием магнитного поля. Отличительной особенностью данной математической модели является учет времени релаксации частицы и изменяющейся в зависимости от радиуса тангенциальной составляющей скорости среды. Благодаря этому достигается большая точность при моделировании кинетики коагуляции ферромагнитных частиц при криволинейном движении.
Библиографическая ссылка
Просвирнин В.И., Масюткин Е.П., Масюткин Д.Е. УТОЧНЕННАЯ МАТЕМАТИЧЕСКАЯ МОДЕЛЬ КОАГУЛЯЦИИ МАГНИТНЫХ ЧАСТИЦ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ // Современные наукоемкие технологии. 2017. № 9. С. 58-63;URL: https://top-technologies.ru/ru/article/view?id=36801 (дата обращения: 27.12.2025).



