Анализируемые процессы используются при разработке различных химических технологий и аппаратов с использованием гидромеханических процессов переноса частиц твердых веществ в жидкости [1]. В рамках общей физико-математической модели процесс движения полидисперсной смеси твердых частиц в горизонтальном трубопроводе рассматривался в работе [2]. Основные положения физико-математической модели движения монодисперсных твердых частиц сферической формы в горизонтальном трубопроводе можно сформулировать в следующем виде [3].
1. Движение потока частиц в потоке жидкости в горизонтальной трубе представляется в виде суперпозиции движений в горизонтальных плоских слоях и плоского слоя в вертикальной диаметральной плоскости трубы.
2. Объемная доля частиц твердой фазы постоянна для каждого горизонтального сечения.
3. Твердые частицы не создают на нижней образующей трубы неподвижный или движущийся слой твердых частиц. То есть рассматривается так называемый критический (гетерогенный) режим гидротранспортирования, при котором образование такого слоя вдоль нижней образующей горизонтальной трубы ещё не происходит, и режимы течения с более высокими гидродинамическими параметрами, при котором распределение твердой фазы стремится к осесимметричному (гомогенному) распределению частиц твердой фазы относительно оси трубы.
4. В продольном направлении движущиеся частицы не сталкиваются друг с другом.
5. В поперечном направлении движущиеся частицы упруго сталкиваются между собой, поскольку, за счет действия разности силы тяжести и Архимеда, частицы перемещаются вниз, а за счет процесса диффузии частицы переносятся снизу вверх.
Методические основы метода расчета
На основе сформулированной физико-математической модели процесса движения твердых частиц в потоке жидкости, конкретный процесс вычислений реализуется следующим образом [3].
Как следует из анализа опытных данных и общих теоретических представлений о гидромеханике двухфазных потоков (см., например [4]) при движении двухфазных смесей из-за значительного изменения концентрации твердой фазы в вертикальной плоскости, динамическая ось потока (место расположения максимума скорости) смещается верх по отношению к геометрической оси трубы. В придонной области течения характерным размером является не радиус трубы, а величина расстояния от дна трубы до динамической оси потока hd, а в верхней зоне течения величина hu – расстояние от динамической оси потока до верхней образующей трубы. Причем hd + hu = D. При гомогенном режиме течения hd = hu = D/2.
При заданном значении градиента давления, из рассмотрения движения плоского турбулентного слоя в вертикальной диаметральной плоскости определяются локальные распределения объемной доли твердой фазы, скорости частиц и жидкости в вертикальном диаметральном сечении. При этом, в рамках распространения модели Прандтля на двухфазные течения, суммарное трение в двухфазном потока представлялось в виде суммы сил трения, возникающих в жидкости при её движении, и сил трения, которые возникают в жидкости при перемещении в ней твердых частиц [2]. Из условия вертикальной симметрии потока следует, что эти скорости будут максимальными для каждого горизонтального сечения. При известных локальных значениях скоростей жидкой и твердой фаз в горизонтальных слоях плоских течений определяются расход жидкой и твердой фаз в горизонтальных сечениях и общий объемный расход.
При установившемся движении двухфазного потока в горизонтальном трубопроводе уравнение движения твердых частиц записывается в виде равенства сил, определяемых величиной градиента давления, действующего на частицу, и гидродинамического трения. В результате определяется скорость движения частицы относительно жидкости. Далее с использованием модифицированной модели Прандтля для турбулентного трения рассчитывается средняя локальная скорость движения двухфазной среды.
При рассмотрении движения частиц в вертикальном направлении принимается, что на частицы, наряду с силами веса и Архимеда, действуют силы Магнуса, Саффмана, которые направлены от стенки трубы в сторону динамической оси потока и знакопеременная сила турбофореза, которая направлена из области максимальных пульсаций скорости потока в область минимальных пульсаций скорости. В результате действия этих сил объемная доля твердых частиц уменьшается при возрастании расстояния от нижней (донной) образующей стенки трубы. При неравномерном распределении объемной доли частиц твердой фазы по вертикальному сечению возникает вертикальный турбулентный диффузионный поток частиц, направленный в противоположную сторону, то есть снизу вверх. В связи с наличием встречных потоков частиц, перемещающихся сверху вниз, за счет указанных выше сил, и переносимых снизу вверх за счет процесса диффузии, учитывается столкновение частиц между собой, которое считается упругим. В области 0 < y < hd на твердые частицы действуют силы Магнуса, Саффмана и Архимеда, направленные вверх, сила тяжести, направленная вниз, и знакопеременная сила турбофореза. Заметим, что поскольку средняя объемная доля частиц в каждом сечении поддерживается постоянной, средняя скорость жидкости в поперечном направлении равна нулю. В области hd ≤ y ≤ D частично изменяется направление действия сил в вертикальном сечении. В частности, силы тяжести, Магнуса, Сафмана направлены вниз, сила Архимеда вверх, а сила турбофореза переменна по направлению. Совокупность получаемых соотношений позволяет рассчитать распределение концентрации по высоте вертикального диаметрального сечения трубы. Положение динамической оси потока определяется из условия, что максимальные значения скоростей, отсчитываемые от нижней Ud и верхней Uu образующих трубы на динамической оси потока, равны с заданной погрешностью. В полном объеме расчетные зависимости приведены в работе [3].
Цель работы
Целью настоящей работы является доказательство возможности расширения области применения метода расчета на движение твердых частиц среднего размера.
Анализ опытных данных
В работе [3] приведены результаты расчета поперечной объемной доли частиц твердой фазы φ – мелкодисперсных частиц песка плотностью 2650 кг/м3 со средними диаметрами 0,090 мм и 0,165 мм в трубопроводах диаметром 102,5 мм, 158,5 мм и 51,5 мм соответственно, опубликованными в работах [5÷7]. Расхождение между расчетными и опытными значениями, как интегральных характеристик потока, так и распределением объемной доли частиц твердой фазы φ в вертикальном диаметральном сечении не превышает 15 %.
В данной работе проводится аналогичное сопоставление с движением монодисперсных частиц песка более крупных фракций в трубопроводе большего диаметра. Расчет основных параметров гидротранспортирования частиц средней крупности, выполненный по изложенному методу [3], сопоставлялся с опубликованными экспериментальными данными и расчетными значениями, приведенными в работе [8]. Проанализируем опытные данные, которые представлены для частиц песка плотностью ρp = 2650 кг/м3 с тремя условными диаметрами d = 0,165 мм, d = 0,290 мм и d = 0,550 мм в трубопроводе с внутренним диаметром D = 263 мм. Первичные опытные данные представлены в виде графических зависимостей: φ = Φ1(y/D) и (–dp/dx) = Ф2(φmid, Umid = const), где φmid – средняя объемная доля частиц в поперечном сечении трубы, (–dp/dx) – градиент давления и Umid – средняя скорость двухфазного потока, определенная по объемному расходу. Из всего объема экспериментальных данных – 16 опытов, выделим 6 опытов, в которых имеется существенное отклонение, не только количественное, но и качественное в распределении объемной доли твердой фазы в вертикальном диаметральном сечении трубы.
В табл. 1 в столбцах указаны значения физических величин, которые были измерены и затем рассчитаны интегрированием по поперечному сечению трубопровода, это величины φmid и Umid. Полужирным шрифтом выделены опытные значения (–dp/dx), которые определялись с соответствующего графика, приведенного в работе [8], при этом погрешность определения величины градиента давления оценивается в ± 25 Па/м. В работе [8] не указаны расчетные значения величин градиента давления, поэтому в табл. 1 они не приведены.
Таблица 1
Сравнение опытных и расчетных интегральных характеристик двухфазных потоков
|
№ п/п |
d, мкм |
Эксперимент [8] |
Расчет [9] |
Расчет по [3] |
||||||
|
φmid |
(–dp/dx), Па/м |
Umid, м/с |
φmid |
(–dp/dx), Па/м |
Umid, м/с |
φmid |
(–dp/dx), Па/м |
Umid, м/с |
||
|
1 |
165 |
0,184 |
360 |
3,5 |
0,184 |
– |
3,5 |
0,183 |
415 |
3,5 |
|
2 |
165 |
0,268 |
400 |
3,5 |
0,268 |
– |
3,5 |
0,267 |
445 |
3,5 |
|
3 |
290 |
0,34 |
665 |
4,0 |
0,34 |
– |
4,0 |
0,339 |
650 |
4,0 |
|
4 |
290 |
0,34 |
830 |
4,7 |
0,34 |
– |
4,7 |
0,34 |
810 |
4,7 |
|
5 |
550 |
0,30 |
920 |
3,9 |
0,30 |
– |
3,9 |
0,293 |
660 |
3,9 |
|
6 |
550 |
0,30 |
1100 |
4,4 |
0,30 |
– |
4,4 |
0,296 |
870 |
4,4 |
Метод расчета, использованный в работе [8], включает коммерческий программный комплекс Computation Fluid Dynamics (CFD), основывающийся на эйлеровой модели двухфазного потока, дополненной моделями турбулентности для жидкой и твердой фаз. Как показывает анализ используемых в [8] зависимостей, при использовании сложных математических моделей необходимо привлечение дополнительных гипотез о представлении и (или) связи различных определяющих параметров, что приводит к использованию полуэмпирических зависимостей, общее число которых может достигать десяти и более. Как будет показано ниже, априори это не обеспечивает наилучшего соответствия с опытными данными. Отметим, что в работе [2] показано, что аналогичное положение имеет место и при сравнении опытных данных по полидисперсным потокам, приведенным в работе [9], с результатами расчетов авторов и методом расчета, изложенным в работе [2].
Результаты сопоставления опытных и расчетных данных
Из данных, приведенных в табл. 1, следует, что расчетные интегральные характеристики рассмотренных двухфазных потоков: φmid, (– dp/dx) и Umid достаточно удовлетворительно согласуются с опытными данными. При этом отклонения по величине (–dp/dx) по предложенному методу расчета в сравнении с опытными данными возрастают при увеличении диаметра частиц.
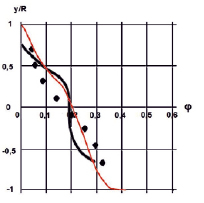
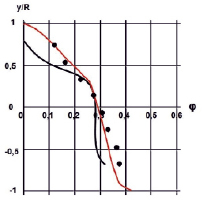
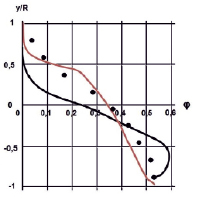
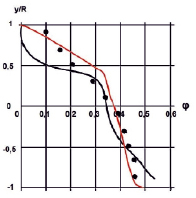
На рис. 1 и 2 приведены распределения объемной доли твердой фазы для частиц с размером d = 165 мкм. Из результатов сравнений известного [8] и используемого метода расчета [3] следует, что используемый метод заметно лучше согласуется с опытными данными вблизи во всей области течения, как при φmid = 0,184, так и, в еще большей степени, при φmid = 0,268. В последнем случае можно отметить, что расчетные данные работы [8] значительно, до 25 %, отличаются от опытных данных, вблизи нижней образующей трубы и, в кратность (на порядок), вблизи верхней образующей трубы. Поэтому в последнем случае можно говорить, лишь о качественном соответствии между опытом и расчетом в [8].
|
|
|
|
Рис. 1. Распределение объемной доли твердой фазы φ вертикальном диаметральном сечении трубы для d = 0,165 мм и φmid = 0,184 |
Рис. 2. Распределение объемной доли твердой фазы φ вертикальном диаметральном сечении трубы для d = 0,165 мм и φmid = 0,269 |
|
|
|
|
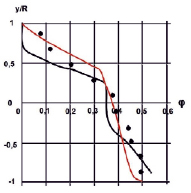
Рис. 3. Распределение объемной доли твердой фазы φ вертикальном диаметральном сечении трубы для d = 0,290 мм и φmid = 0,34 и Umid = 4 м/с: опыт ? [8], расчет по – [8], – расчет по [3] |
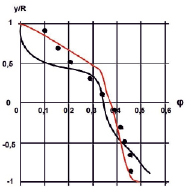
Рис. 4. Распределение объемной доли твердой фазы φ вертикальном диаметральном сечении трубы |
На рис. 3 и 4 приведены распределения объемной доли твердой фазы для частиц с размером d = 0,290 мм. Как и в предыдущем случае, предложенный метод лучше согласуется с опытными данными, нежели метод расчета работы [8], особенно вблизи верхней образующей трубы при Umid = 4,0 м/с. Примерно такое же положение сохраняется и при Umid = 4,7 м/с.
Следует отметить, что горбообразный характер расчетных кривых по [8], показанный на рис. 1–4, имеет место не только на представленных расчетных зависимостях, но и в расчетах с другими параметрами по φmid и Umid, которые приведены в [8], что даже качественно не согласуется с сопоставляемыми опытными данными по распределению объемной доли твердой фазы в вертикальном диаметральном сечении трубы, хотя авторы и считают соответствие расчетных значений с опытом удовлетворительным.
На рис. 5 и 6 приведены распределения объемной доли твердой фазы для частиц с размером d = 0,550 мм. Предложенный метод лучше согласуется с опытными данными, нежели метод расчета работы [8], особенно вблизи верхней образующей трубы при Umid = 3,9 м/с. Примерно такое же положение сохраняется и при Umid = 4,4 м/с.
|
|
|
|||
|
Рис. 5. Распределение объемной доли твердой фазы |
Рис. 6. Распределение объемной доли твердой фазы φ вертикальном диаметральном сечении трубы |
|||
|
d, мм |
0,165 |
0,290 |
0,550 |
|
|
φmid |
0,184 |
0,268 |
0,34 |
0,30 |
|
Umidcr, м/с [11] |
2,58 |
3,47 |
5,49 |
6,02 |
|
Umidcrм/с [4] |
3,10 |
3,20 |
3,85 |
4,24 |
|
Umidcrм/с [10] |
2,90 |
3,09 |
3,71 |
4,01 |
Библиографическая ссылка
Кондратьев А.С., Швыдько П.П. ГИДРОТРАНСПОРТИРОВАНИЕ МОНОДИСПЕРСНЫХ ЧАСТИЦ СРЕДНЕЙ КРУПНОСТИ ПО ГОРИЗОНТАЛЬНЫМ ТРУБАМ // Современные наукоемкие технологии. 2017. № 9. С. 28-33;URL: https://top-technologies.ru/ru/article/view?id=36796 (дата обращения: 01.01.2026).