Продукция нефтяных скважин представляет собой многофазную смесь нефти, газа, механических примесей (песок, глина, известняк и др.) и пластовой воды, в которой растворены различные соли. Очевидно, что такую «грязную» и сырую нефть, содержащую к тому же легколетучие органические (от метана, этана и др.) и неорганические (Н2S, СО2 и др.) газовые компоненты, нельзя транспортировать без тщательной ее промысловой подготовки. Одним из актуальных вопросов исследования в нефтегазовой промышленности является процесс отделения воды и газа от сырой нефти. Данный процесс в большой степени определяет качество нефти, которая доставляется на нефтеперерабатывающие заводы [1]. На скважинах часто применяется многоступенчатое разделение нефти.
Практика показывает, многоступенчатая подготовка нефти является многокомпонентным процессом, в котором применяемые технологии и аппараты неэффективны. Некачественное обезвоживание и дегазация нефти ведет к коррозии и дальнейшей неработоспособности трубопроводов, остатки газа выделяются в процессе хранения и транспортировки нефти, выводят из строя оборудование промыслов, образуют взрывоопасные очаги и загрязняют окружающую среду, также вместе с газом улетучиваются и ценные легкие бензиновые фракции [2, 3].
Причина неудовлетворительной работы аппаратуры по подготовке нефти связана в основном, с отсутствием их всесторонней математической и алгоритмической проработки.
Главными направлениями повышения качества разделения многофазных смесей являются разработка новых способов, устройств и технологических линий, создание и использование систем автоматического управления (регулирования) технологическим процессом. Для интенсификации процесса разделения многофазной смеси предлагается применять способ, который совмещает гидродинамические и тепломассообменные процессы с использованием центробежного воздействия [4–6].
Постановка цели исследования
Цель работы заключается в повышении эффективности управления процессом разделения многофазной смеси с помощью внешних воздействий, обеспечивающих разрыв сплошности потока.
Одним из параметров процесса разделения многофазной смеси является поверхностное натяжение системы газ – жидкость, способствующее образованию устойчивых эмульсий и удержанию газа. Поэтому необходимо уменьшить поверхностное натяжение системы.
Для решения поставленной задачи необходима разработка новой модели, которая учитывала бы комплексное влияние сил поверхностного натяжения на условия разрыва сплошности потока. Поверхностью разрыва называют неоднородную область между соприкасающимися фазами [7]. При этом в фазах неоднородность проявляется в этой области на межмолекулярных расстояниях, в отличие, например, от воздействия гравитационного или другого внешнего силового поля. Поэтому говорят о скачке (разрыве) ряда свойств на границе фаз.
Рассмотрим способ разделения многофазной смеси, который связан с разрушением водогазонефтяной эмульсии под воздействием центробежных сил. В его основу положено течение пленки вязкой жидкости по поверхности вращающегося диска [8]. При этом необходимо создать постоянный расход смеси поступающей на вращающийся диск, характерный размер которого обеспечивает создание критической резонансной толщины образованного слоя жидкости, а также снижение эффективной вязкости до наименьшего значения [9]. Эти условия позволяют провести глубокое разделение многофазной смеси, а также повысить дегазацию.
Теория исследования
Движение вязких несжимаемых жидкостей описывается уравнением Навье – Стокса. Уравнения Навье – Стокса являются одними из важнейших в гидродинамике и применяются в математическом моделировании многих природных явлений и технических задач [10].
Точные общие аналитические решения системы Навье-Стокса для пространственного или плоского потока – нелинейные и сильно зависят от начальных и граничных условий.
Пусть по оси вращения диска подается с постоянным расходом вязкая несжимаемая жидкость (многофазная смесь) (рис. 1). Вязкая жидкость вращается с угловой скоростью w относительно оси z в цилиндрической системе координат (r, j, z), начало которой совмещено с центром диска.
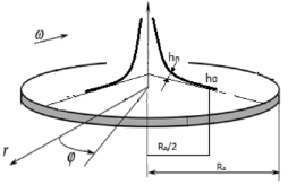
Рис. 1. Схема движения жидкости
Введем обозначение vr, vφ, vz – составляющие скорости течения соответственно в радиальном направлении r, в окружном направлении j и в осевом направлении z, через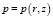 
– давление.
Считаем, что жидкость вязкая, несжимаемая, ньютоновская, движение ламинарное, тепло-физические свойства жидкости постоянны, толщина слоя меньше радиуса его растекания, давление постоянно.
Граничные условия, с одной стороны, определяются условиями прилипания к вращающейся поверхности: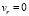 
, 
, 
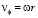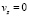при z = 0, а с другой стороны, при z, равном некоторой конечной величине 
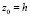(где h – высота слоя жидкости), в зависимости от рассматриваемой задачи могут принимать различные выражения.
Запишем уравнение Навье – Стокса в цилиндрической системе координат:
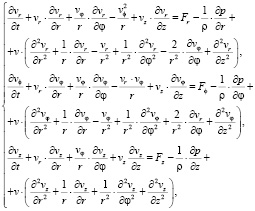(1)
где vr, vφ, vz – соответственно радиальная, тангенциальная и нормальная компоненты относительной скорости, м/с; Fr, F?, Fz – проекции массовых сил на оси координат; t – время, с; р – давление, Па; v – кинематическая вязкость, м2/с; ρ – плотность, кг/м.
В общем виде решение системы уравнений (1) получить невозможно, что связано с математическими трудностями.
В рассматриваемом случае теоретической основой послужила система, состоящая из уравнений движения, неразрывности и баланса масс (2), полученная путем наложения условий на уравнения (1). Приняты допущения: жидкость несжимаема, толщина слоя значительно меньше радиуса его растекания, внезапные ускорения отсутствуют, существенен только градиент давления в радиальном направлении, w – угловая скорость вращения пластины, наклоненной под углом α. Кроме того, логично положить для рассматриваемых задач, что массовые силы Fr = F? = Fz = 0.
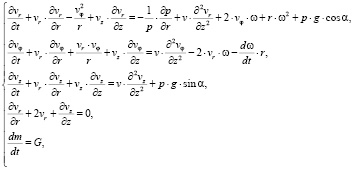(2)
где т – масса многофазовой смеси, кг; G – массовый расход многофазовой смеси, кг/с.
Начальные условия:
t = 0; vr = vr0, vφ = vω0, vz = vz0, m = m0,
где t – время протекания процесса, с; vr0, vp0, vz0 – начальные значения компонент относительных скоростей (по координатам r, φ, z), м/с; m0 – начальная масса многофазной смеси, поступающей на диск, кг.
Граничные условия:
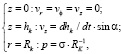(3)
где σ – коэффициент поверхностного натяжения жидкости, Н/м.
Учитывая влияние сил поверхностного натяжения, вязкостных и инерционных сил для течения тонких пленок, получим
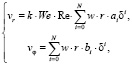(4)
где ai, bi, δ = z·h-1 – безразмерные функции времени и координаты;
k – поправочный коэффициент.
We = σ -1·ρ·ω2·R2k·hK – число Вебера;
Re = ω·RK·hK·v-1 – число Рейнольдса.
Исходя из цели исследования, необходимо обеспечить разрыв сплошности потока в центральной части вращающегося диска (Rд/2). Разрыв определяется с использованием соотношения сил поверхностного натяжения и центробежных сил, которое характеризуется числом Вебера. Разрыв сплошности потока происходит при значении We ≤ Weкр критического. Используя выражение для определения числа Вебера, найдем Rкр, с помощью которого определим границу области разрыва сплошности потока:
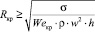. (5)
При этом необходимо учитывать, что разрыв сплошности потока происходит, когда центробежные силы превышают силы поверхностного натяжения.
Критерий разрыва сплошности потока может быть получен на основе чисел Вебера и Рейнольдса:
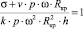. (6)
Из формулы (6) находим угловую скорость вращения диска:
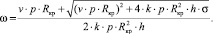(7)
Так как для эффективного разделения многофазной смеси необходимо поддерживать расход постоянным, будем рассматривать установившееся движение. Тогда производные по времени равны нулю,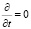 
.
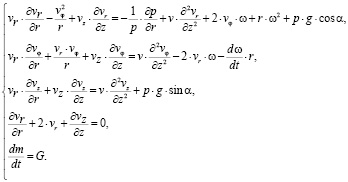(8)
Растекание пленки рассматривается как задача Коши с формулируемыми ниже начальными условиями при r = 0.
Для численного решения (2) вводятся линии тока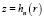 
и значения компонент скорости на них 
, 
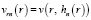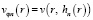, n = 1, 2, …, N, причем 
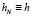. Для расходов 
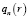, определяемых соотношениями
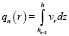, n = 1, 2, …, N, 
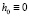, (9)
из уравнения неразрывности и условий непротекания через линии тока следует
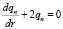, n = 1, 2, …, N. (10)
Используя для вычисления интегралов (9) формулу трапеций, из (10) можно получить
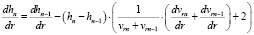, (11)
n = 1, 2, …, N,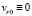 
.
Уравнения движения, записанные на линиях тока, дают
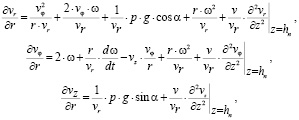(12)
n = 1, 2, …, N.
Для вычисления входящих в правые части (12) вторых производных применяется тау-аппроксимация с использованием смещенных полиномов Чебышева первого рода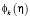 
, определяемых формулами:
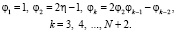
При этом для компонент скорости строится аппроксимирующая функция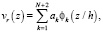 
коэффициенты разложения которой ak, k = 1,2,…, N + 2, являются решениями системы линейных алгебраических уравнений
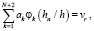n = 1, 2, …, N, (13)
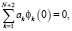
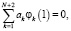(14)
где (13) – условия равенства функции vrN значениям компоненты скорости vr на линиях тока, (14) – аппроксимация граничных условий на диске и поверхности пленки соответственно.
Выражая для вторых производных функции vr на линиях тока имеют вид
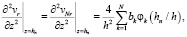
n = 1, 2, …, N,
где
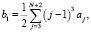
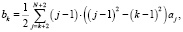
k = 2, 3, …, N.
К уравнениям (11), (12) добавляются начальные условия:
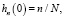
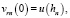
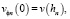
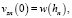
n = 1, 2, …, N,
где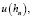 
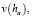
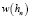– заданные функции.
Точность вычислений определяется числом линий тока и сложностью профилей компонент скорости.
Из решения уравнений (12) и подставляя в (6) следует, что расход многофазной смеси в устройстве с вращающимися дисками можно определить по формуле
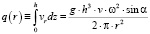. (15)
Заключение
В результате вычислений получили основные зависимости (7 и 15), влияющие на производительность установки по разделению многофазной смеси при помощи вращающихся дисков.
Конструкция установки с полученной математической моделью представлена на рис. 2.
Рис. 2. Конструкция установки с вращающимися дисками
Таким образом, для конструкции установки с вращающимися дисками оптимизированным параметром является скорость вращения дисков, которая зависит от основных характеристик (коэффициент поверхностного натяжения и кинематическая вязкость жидкости) и количества дозирования смеси. В условиях постоянно изменяющихся физико-химических свойств многофазной смеси такая модель установки является наиболее приемлемой, так как нет необходимости переналадки оборудования технологического процесса, достаточно только изменить скорость вращения дисков. При автоматизированном процессе разделения многофазной смеси можно в режиме «реального времени» поддерживать технологические параметры в нормальных условиях, при которых процесс разделения будет идти с максимальным выделением газа и примесей из многофазной смеси.
Библиографическая ссылка
Тугов В.В. УПРАВЛЕНИЕ ПРОЦЕССОМ РАЗДЕЛЕНИЯ МНОГОФАЗНОЙ СМЕСИ С ИСПОЛЬЗОВАНИЕМ ЦЕНТРОБЕЖНОГО ВОЗДЕЙСТВИЯ // Современные наукоемкие технологии. – 2017. – № 8. – С. 69-74;URL: https://top-technologies.ru/ru/article/view?id=36782 (дата обращения: 20.04.2024).