При градостроительстве зачастую возникают задачи ликвидации так называемых долгостроев [1]. Одним из видов работ, выполняемых для этого, является извлечение свай из грунта [2]. Многие из существующих методов, решающих эту задачу, трудно применимы при точечной застройке зданий. На рисунке приведена артиллерийская установка для застреливания анкеров и свай в грунт УЗАС-2 [3], которая создана в г. Перми. При извлечении свай из грунта возможно использование установки следующим образом. В ствол помещается штамп с большой площадью миделевого сечения основания. К откатным частям пушки жестко прикрепляется голова извлекаемой из грунта сваи. Во время выстрела штамп на небольшую глубину проникает в грунт, а откатные части пушки поднимаются вверх, извлекая сваю из грунта. В настоящей статье решается задача моделирования динамики одноствольных артиллерийских систем, и в частности УЗАС-2, при извлечении свай из грунта.
Математическая модель
Для разработки математической модели будем основываться на термодинамической теории выстрела в рамках допущений этой теории [4, 5] при использовании трубчатого зерненого пороха.
Предварительный период выстрела описывается известной формулой
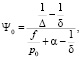 (1)
(1)
где Δ – плотность заряжания, δ – плотность пороха, f – сила пороха, р0 – давление форсирования штампа, α – коволюм пороховых газов.
Будем предполагать, что перед выстрелом штамп упирается в грунт.
При анализе процесса выстрела во время застреливания штампа в грунт необходимо учитывать не только часть энергии пороховых газов, которая превращается в кинетическую энергию поступательного движения строительного элемента, но и энергию, затрачиваемую на совершение другого вида работ. Это позволит установить полный баланс энергии при выстреле [6].

Установка УЗАС-2 с застреливаемым
в грунт штампом
Определим работу по преодолению силы сопротивления грунта движению в нем штампа, выполненную за счет энергии пороховых газов.
Пусть va – абсолютная скорость штампа, la – абсолютный путь штампа по каналу ствола. В этих обозначениях силу сопротивления грунта F можно записать в виде соотношения
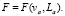
Тогда энергию, необходимую для вдавливания штампа на глубину La, можно записать в виде
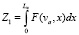 ,
,
где 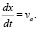
Таким образом, величина Z1 примет вид
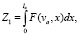
где 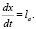
Очевидно, что кинетическая энергия, которую будет иметь штамп массой m в момент времени t, удовлетворяет соотношению
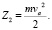
Напомним, что ствол артиллерийской системы расположен вертикально и таким образом, что штамп движется вниз. То есть очевидно, что энергия пороховых газов идет на перемещение откатных частей артиллерийского орудия вверх. Таким образом, совершается работа, которую можно выразить соотношением
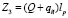 ,
,
где Q – вес откатных частей артиллерийского орудия, qc – вес извлекаемой сваи, lp – перемещение откатных частей.
Кроме того, энергия пороховых газов сообщает откатным частям артиллерийского орудия и извлекаемой сваи скорость V. Следовательно, кинетическая энергия откатных частей удовлетворяет равенству
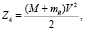
где M – масса откатных частей пушки, mc – масса сваи.
Энергия, расходуемая на преодоление силы сопротивления отката, имеет вид
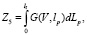
где lp – путь отката, 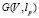 – сила сопротивления отката.
– сила сопротивления отката.
Так как штамп движется вертикально вниз, то сила тяжести сама выполняет работу
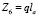 ,
,
которая не входит в сумму работ, совершаемых за счет энергии пороховых газов.
Пусть E – энергия пороховых газов, за счет которой совершаются работы Z1, Z2, Z3, Z4, Z5. Тогда очевидно соотношение
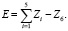 (2)
(2)
Известно [6], что величину Е можно аппроксимировать в следующем виде:
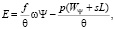 (3)
(3)
где θ – коэффициент адиабаты пороховых газов без единицы, ω – масса заряда, Ψ – относительная часть сгоревшего заряда, Р – давление в канале ствола, WΨ – свободный объем каморы к моменту сгорания в ней части заряда Ψ, s – площадь поперечного сечения канала ствола, L – путь штампа по каналу ствола.
Заменяя в соотношении (2) значения Zi их алгебраическими выражениями и учитывая формулу (3), получим равенство
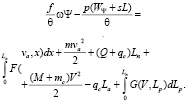 (4)
(4)
Из уравнения (4) получаем, дифференцируя параметр давления в канале ствола p по времени t, соотношение
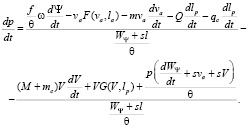 (5)
(5)
Очевидны следующие уравнения, описывающие поступательное движение штампа, откатных частей пушки и извлекаемой сваи:
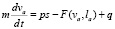 , (6)
, (6)
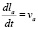 , (7)
, (7)
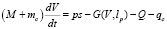 , (8)
, (8)
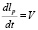 . (9)
. (9)
Согласно закону горения трубчатого зерненого пороха [5] справедливы соотношения
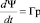 ,
, 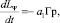 (10)
(10)
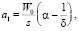
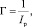
где Ip – полный импульс давления пороховых газов за время сгорания пороха.
Начальные условия для решения системы дифференциальных уравнений (5)–(10) запишутся в виде
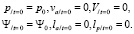
Согласно термодинамической теории выстрела задача Коши [7], описывает первый период выстрела [6].
Уравнения второго периода выстрела [5] эквиваленты уравнениям первого периода выстрела при условии Ψ ≡ 1. Уравнение
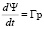
в систему уравнений не войдет. Начальные условия для решения системы обыкновенных дифференциальных уравнений для второго периода выстрела равны конечным значениям искомых функций задачи Коши, описывающей первый период выстрела.
Численный эксперимент
В качестве исходных параметров для проведения численного эксперимента примем следующие характеристики.
Рассмотрим глинистый грунт с консистенцией 0,3.
Сила сопротивления этого грунта (Н) прониканию штампа определяется соотношением [3]:
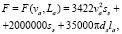
где ss, ds – площадь миделевого сечения и диаметр штампа, м.
Сила сопротивления отката (Н) удовлетворяет равенству
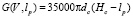 ,
,
где Hc – первоначальное заглубление извлекаемой сваи.
Для численного решения задачи динамики выстрела примем следующие характеристики орудия, условия заряжания, параметры штампа и извлекаемой сваи: длина канала ствола – 1,8 м, вес заряда – 3 н, калибр ствола – 0,170 м, объем каморы – 0,001026 м3, сила пороха – 950000 дж/кг, плотность пороха – 1600 кг/м3, показатель адиабаты пороховых газов – 1,2, коволюм пороховых газов – 0,98 10-3 м3/кг, полный импульс давления газов во время сгорания пороха (импульс пороха) – 376500 Па с, вес откатных частей орудия – 36000 н, диаметр головной части штампа – 0,5 м, масса штампа – 800 кг, диаметр извлекаемой сваи – 0,168 м, масса сваи – 240 кг, первоначальное проникание сваи – 4 м.
Для расчета динамики орудия была разработана специальная программа. Для решения задач Коши использовался метод Рунге – Кутты 2-го порядка [6] с шагом интегрировании 10-6 с [3, 4]. Вычисления проводились согласно последовательности: формула (1) – уравнения (2)–(10) – уравнения второго периода выстрела.
Вычисления позволили получить следующие динамические показатели к концу выстрела: максимальное давление в канале ствола – 654 МПа, дульное давление пороховых газов – 4,2 МПа, величина проникания штампа в грунт – 1,13 м, величина извлечения сваи из грунта – 3,46 м.
Заключение
Таким образом, в статье на основе построенной математической модели и численных расчетов показана принципиальная возможность применения одноствольных артиллерийских орудий для извлечения свай из грунта.
Библиографическая ссылка
Пенский О.Г. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ИЗВЛЕЧЕНИЯ СВАЙ ИЗ ГРУНТА С ПОМОЩЬЮ ОДНОСТВОЛЬНЫХ АРТИЛЛЕРИЙСКИХ СИСТЕМ // Современные наукоемкие технологии. 2017. № 8. С. 46-49;URL: https://top-technologies.ru/ru/article/view?id=36778 (дата обращения: 13.02.2026).



