Одной из задач, возникающих на финансовом рынке, является управление финансовым риском. Существуют различные инструменты и подходы для управления риском. Эффективным инструментом для управления финансовым риском являются опционы. Указанная эффективность обуславливается их свойством защиты владельца от неблагоприятного исхода, а в случае благоприятного исхода возможность получения дополнительной прибыли. Однако возникает задача определения справедливой цены опциона (подробнее об опционах см. [1]).
Если рассматривать поведение цен рисковых активов, их траекторию, можно заметить, что в поведении цен рисковых активов наблюдаются скачки (рис. 1, данные приведены из [2]).
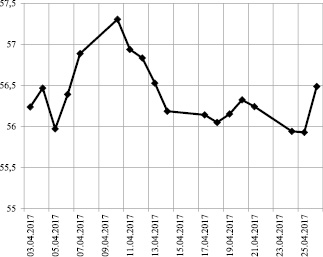
Рис. 1. Средневзвешенный курс (руб./долл.). Расчет «сегодня»
Для моделирования цен на финансовом рынке будем использовать процессы Леви, поскольку они обладают широким набором математических свойств, так как траектории указанных процессов имеют скачки. Процессы Леви используются для моделирования различных объектов в разных сферах деятельности, в том числе и для моделирования поведения цен рисковых активов, но здесь возникает ряд сложностей, которые обусловлены неполнотой рассматриваемого (B,S)-рынка.
Цель исследования
Целью исследования, приведенного в данной статье, является получение метода вычисления цен опционов для дискретизированных процессов Леви в случае конечной меры Леви.
Материалы и методы исследования
Определение цены опционов можно рассматривать как задачу вычисления условного математического ожидания.
Будем считать, что дисконтированная цена рискового актива является экспоненциальным процессом Леви (1):
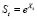, Xt – процесс Леви. (1)
Введем обозначение: f – дисконтированное финансовое обязательство (опцион можно рассматривать как ограниченную функцию).
Тогда задача определения безарбитражной цены хеджирования финансового обязательства (которое является дисконтированным) в момент времени t, если в данный момент времени дисконтированная цена рискового актива равна S:
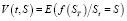. (2)
Если мера является мартингальной (риск-нейтральной), то задача (2) решается. Если исходная мера не является мартингальной, то сначала необходимо перейти к эквивалентной мартингальной мере (подробнее см. [3]).
Применяя свойства процесса Леви, задачу (2) можно рассматривать в виде
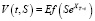. (3)
Рассмотрим дискретизацию экспоненциального процесса Леви St. Отметим, что данный вид дискретизации применяется, если мера Леви конечна.
Будем рассматривать регулярные промежутки времени при дискретизации по времени: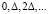 
, тогда получим случайное блуждание 
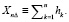Тогда случайные величины 
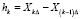– одинаково распределенные, их распределение совпадает с распределением XΔ, является безгранично делимым. В итоге, указав шаг дискретизации, получаем семейство случайных блужданий XnΔ (случайные блуждания с пропущенными шагами рассмотрены в [4]).
После дискретизации по времени процесс St поведения рискового актива, (1) перепишем в
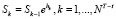. (4)
Естественная фильтрация имеет вид
.
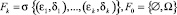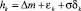. (5)
Процесс (4) – дискретизированный по времени процесс Леви на интервале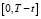 
с достаточно малым шагом дискретизации 
, 
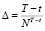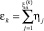, εk независимы, 
, 
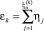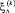– независимые и одинаково распределенные случайные величины по закону Пуассона с интенсивностью λΔ, ηj − независимые и одинаково распределенные случайные величины с законом распределения F(dx), δk - стандартные нормальные величины, 
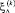и δk − независимые случайные величины.
Соотношение для определения ? при заданной точности α имеет вид
.
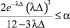Если величина шага дискретизации ? является достаточно малой величиной, то со степенью точности α можно считать, что число скачков на каждом интервале разбиения скачок или есть, или скачка нет, то есть невозможной является ситуация, когда на интервале будет не менее двух скачков.
В [6] был предложен подход для случая бесконечной меры Леви.
Тогда (5) примет вид
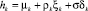, (6)
, 
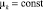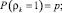
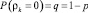; ξk − независимая случайная величина, закон распределения – F(dx); δk − стандартные нормальные величины; случайные величины ρk, ξk, δk являются независимыми.
В данном случае фильтрация будет следующая:
.
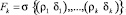Рассмотрим два случая:
1) ξk (скачок) в формуле (6) изменяется по закону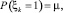 
, 
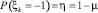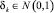, N = 20, T = 10, σ = 0,05 (рис. 2);
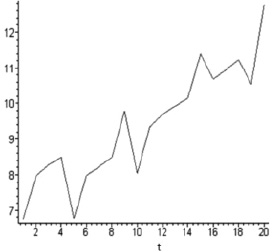
Рис. 2. Изменение hk. Ситуация 1
Рис. 3. Изменение hk. Ситуация 2
2) скачок в формуле (6) изменяется по экспоненциальному закону,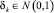 
, N = 20, T = 10 (рис. 3). Рис. 2 и рис. 3 отражают эволюцию индекса hk, который имеет скачки в случайные моменты времени.
Определим условие мартингальности для процесса (4) и hk изменяются по закону (6). Условие мартингальности имеет вид
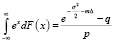. (7)
Заметим, что если не выполняется условие (7), то необходимо переходить к мартингальной мере. Для этого можно использовать преобразование Гирсанова или Эшера.
Преобразование Гирсанова для моделей (4) будем искать при помощи процесса плотности:
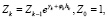
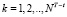. (8)
Преобразование Эшера для моделей (4) имеет вид (подробнее о преобразовании Эшера [5, 6]):
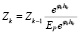. (9)
Для моделей (4), как было показано в [6], преобразование Эшера и Гирсанова совпадают.
Для параметра преобразования Эшера должно выполняться соотношение
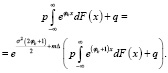(10)
Если в (6) случайные величины ξk распределены по закону Пуассона, интенсивность равна λ, тогда (6) примет вид
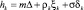. (11)
Условие (7) примет вид
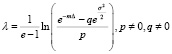. (12)
Условие для параметра преобразование Эшера:
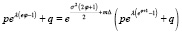. (13)
В случае выполнения условия для мартингальной меры, условие для интервала дискретизации имеет вид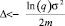 
.
Рассмотрим случай (11), если (6) имеет вид
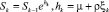. (14)
Тогда исходя из условия мартингальности, соотношение для определения интервала дискретизации имеет вид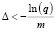 
.
Результаты исследования и их обсуждение
Рассмотрим задачу перехода к мартингальной мере (определения цены хеджирования, дисконтированное финансовое обязательство можно рассматривать как опцион европейского типа):
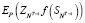. (15)
Введем допущение: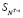 
эволюционирует по закону (4) и hk изменяется по закону (5).
; 
; 
; 
.
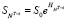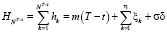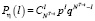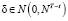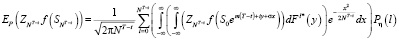, (16)
где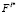 
– l-кратная свертка распределения F с собой.
Пример 1. Если hk изменяется согласно (11), тогда
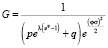, (17)
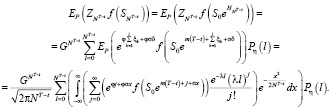
Следовательно, (16) примет вид
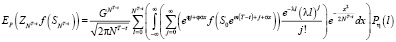. (18)
Напомним, что мы получили аналитическую формулу в случае конечной меры Леви для определения цены хеджирования опциона Европейского типа.
Пример 2. Рассмотрим случай, если в (6) ξk будет независимой случайной величиной, распределенной по симметризованному геометрическому закону распределения.
Проведем симметризацию геометрического закона распределения, используя подход, предложенный в [7]:
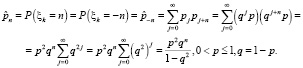
Исходная мера является мартингальной, если выполнено условие
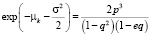. (19)
Плотность представляется в виде
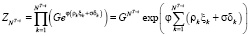, (20)
где φ – параметр преобразования Эшера,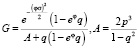 
.
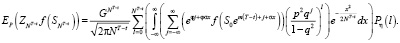(21)
Заключение
В статье предложен численный метод вычисления цен опционов в моделях (B,S)-рынка, который является стохастическим аналогом метода сеток с равномерным шагом. В данном методе шаг выбирается в зависимости от индивидуальных свойств процесса Леви. В результате применения указанного метода получена аналитическая формула для определения безарбитражной цены хеджирования дисконтированного финансового обязательства (опцион Европейского типа). Наличие аналитической формулы существенно упрощает вычислительный процесс, позволяет при вычислении цен опционов не использовать метод деревьев, который обладает достаточно большой вычислительной сложностью, для уменьшения которой необходимо переходить к параллельным вычислениям. Заметим, что в данном случае мера Леви является конечной. Кроме того, появляется возможность проведения различных видов анализа на основе аналитической формулы. В случае, если мера является бесконечной, то возникает ряд сложностей с получением аналитической формулы. Для данного случая численный метод вычисления безарбитражной цены дисконтированного финансового обязательства отличается от сеточных методов. Указанный метод приводит к случайному разбиению временной шкалы.
Библиографическая ссылка
Никоненко Н.Д. ВЫЧИСЛЕНИЕ ЦЕН ОПЦИОНОВ В МОДЕЛЯХ СО СКАЧКАМИ // Современные наукоемкие технологии. – 2017. – № 8. – С. 35-40;URL: https://top-technologies.ru/ru/article/view?id=36776 (дата обращения: 21.11.2024).