На современном этапе развития производства Российской Федерации общество остро нуждается в специалистах, способных решать технические задачи самой разной сложности. Важную роль в подготовке таких специалистов играют высшие и средние специальные учебные заведения.
В основе подготовки бакалавров разных технических направлений заложено множество учебных дисциплин. Одной из важнейших дисциплин, с опорой на знания которой решаются главные инженерные задачи, является теоретическая механика. В результате изучения данного курса студент должен овладеть навыками решения различного рода инженерных задач, что в свою очередь является необходимым при изучении последующих курсов: сопротивление материалов, теория механизмов и машин, детали машин, механика жидкости и газов и т.д.
Цель исследования
Разработать методику поэтапного формирования у студентов, обучающихся по техническим направлениям подготовки, энергетического метода решения физических задач, позволяющего решить широкий круг разнообразных инженерных проблем.
Методы исследования
Анализ существующих методик обучения студентов методам решения физических задач, выявление основных типов задач, решаемых с применением знаний теоретической механики, проведение обучающего педагогического эксперимента и анализ его результатов.
Результаты исследования и их обсуждение
Дисциплина «Теоретическая механика» является основой физико-технической подготовки будущих инженеров. По этой дисциплине существует множество учебников, в которых после изложения теоретического материала приводятся образцы решения конкретных задач. Многолетний опыт преподавания курса «Теоретическая механика» показывает, что ознакомление с готовыми решениями не самый лучший способ освоения теоретической механики. Поэтому у студентов необходимо сформировать обобщенные методы решения основных задач теоретической механики, с применением которых можно решить любую задачу.
В теоретической механике можно выделить следующие основные типы задач:
1. Нахождение кинематических параметров движущегося тела (или любой его точки) в любой момент времени.
2. Прямая задача динамики. Нахождение равнодействующей сил, приложенных к точке, при условии, что заданы масса точки и уравнения её движения.
3. Обратная задача динамики. Записать уравнение движения точки, зная силы, действующие на материальную точку её массу, а также начальное положение и начальную скорость точки.
4. Нахождение скорости точки или приложенных к ней сил с применением теоремы об изменении количества движения.
5. Нахождение параметров движущегося тела или точки с применением энергетического метода.
6. Задача о равновесии: установление условий, при которых тело или система тел находится в равновесии.
7. Задача о приведении системы сил: как данную систему сил заменить другой наиболее простой эквивалентной ей [1].
Остановимся на методике обучения студентов решению задач с применением энергетического метода. Энергетический метод представляет собой систему действий, последовательное выполнение которых позволяет получить уравнение, связывающее изменение механической энергии тела с причиной, вызвавшей это изменение. Для применения данного метода студентам необходимо усвоить следующие знания:
- энергия характеризует состояние системы взаимодействующих тел;
- энергия тела может изменяться; это происходит при переходе тела из одного состояния в другое;
- величина изменения энергии тела зависит от того, является ли система взаимодействующих тел замкнутой и определяется по величине работы неконсервативных сил;
- потенциальная энергия тела является величиной относительной и её величина зависит от выбора нулевого уровня потенциальной энергии, который выбирается произвольно.
Для достижения поставленной цели с помощью этих средств необходимо выполнить следующую систему действий:
1. Изобразить графическую модель ситуации задачи, указав два состояния материальной точки.
2. Выбрать нулевой уровень потенциальной энергии.
3. Найти значение энергии в начальном и конечном состояниях.
4. Найти изменение энергии.
5. Установить является ли система замкнутой, если да, то найти работу внутренних сил.
6. Если система незамкнутая, то найти работу внешних сил.
7. Записать закон сохранения или изменения полной механической энергии [1].
Чтобы студенты овладели энергетическим методом решения физических задач, необходимо провести их через следующие этапы обучения:
1) этап формирования отдельных действий, входящих в содержание энергетического метода;
2) подготовительный этап, на котором происходит решение задач под руководством преподавателя и студенты отрабатывают способы выполнения отдельных действий формируемого метода;
3) методологический этап, на котором происходит выделение и усвоение энергетического метода;
4) этап самостоятельного решения физических задач с применением энергетического метода в обобщенном виде [2]. Данная методика обучения основывается на теории поэтапного формирования умственных действий. Её эффективность при обучении физике неоднократно доказана в работах С.В. Анофриковой, Г.П. Стефановой [3].
Рассмотрим содержание каждого этапа. Цель первого этапа заключается в формировании отдельных действий метода. Начать обучать студентов выполнению действий целесообразно при изучении раздела «Динамика» следующих тем: «Работа», «Кинетическая энергия», «Потенциальная энергия», «Закон сохранения механической энергии». При введении понятий: работа, кинетическая энергия, потенциальная энергия подбираются задачи-упражнения, цели которых совпадают с целями выполнения каждого действия; разрабатывается способ выполнения этих действий и организуется их формирование через многократное выполнение действия в конкретных ситуациях. Данная методика по формированию отдельных действий метода и метода в целом также применяется неоднократно при обучении студентов инженерных специальностей, что отражено в работах О.В. Мирзабековой, М.А. Михайловой, А.В. Хохлова [4], А.Г. Валишевой, И.А. Крутовой [5].
Приведем пример задания и пяти задач-упражнений для формирования шестого действия метода [6, 7].
Задание. Рассчитать работу сил в следующих ситуациях.
1. Какую работу совершает строитель, передвигая по горизонтальному полу на расстояние 5 м горизонтально направленным усилием ящик с цементом массой 45 кг? Коэффициент трения равен 0,4.
2. Тело М весом 50 Н равномерно перемещается вверх по наклонной плоскости длиной 4 м и углом подъема 20 °. Найти работу, произведенную силой, направленной параллельно основанию наклонной плоскости, если коэффициент трения равен 0,4.
3. Найти произведенную работу при равномерном передвижении клинчатого ползуна массой 100 кг на расстояние 2,5 м по направляющим, наклоненным к горизонту под углом 15 °. Движущая сила действует параллельно наклонным направляющим; угол заострения ползуна 60 °; коэффициент трения равен 0,35.
4. Найти работу, которую необходимо произвести, чтобы перекатить каток массой 50 кг на расстояние 4 м по горизонтальной негладкой поверхности. Считать, что сила, двигающая каток, приложена к оси катка и горизонтальна. Диаметр катка 20 см; коэффициент трения равен 0,5.
5. Цокольный этаж затопило грунтовыми водами на 1,2 м. Для того чтобы избавиться от воды, была вызвана бригада рабочих с насосом. Если площадь цокольного этажа 30 кв. м, то какую работу совершит насос, выкачивая воду цилиндрической трубой с радиусом 10 см.
Данное задание и условия задач предъявляются студентам на распечатанных листах или высвечивается на экране. Студентам предлагается разработать программу выполнения первого задания. Каждый из студентов предлагает последовательность действий при решении задачи. После обсуждения действий программы они фиксируются студентами в тетрадях и на доске. Затем преподаватель показывает образец выполнения первого задания в соответствии с разработанной программой. Далее организуется самостоятельная работа студентов по выполнению всех задач-упражнений в соответствии с разработанной программой. Пример выполнения задания по разбору первой ситуации представлен в таблице.
Решение ситуации № 1
|
Последовательность действий |
Анализ ситуации |
|
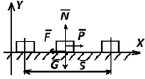
1. Изобразить графическую модель ситуации |
|
|
2. Указать все силы, действующие на исследуемое тело |
Силы указаны на рисунке |
|
3. Выбрать систему отсчета и найти проекции векторов сил на выбранные оси координат |
ОХ: Nx = 0, Gx = 0, Px = P, Fx = –F. OY: Nx = N, Gx = -G, Px = 0, Fx = 0. При равномерном передвижении ящика четыре силы образуют уравновешенную систему и поэтому, спроектировав их на горизонтальную и вертикальную оси, найдем, что P = F и N = G |
|
4. Вывести формулу для нахождения значения работы в конкретной ситуации |
A = Pscosα, так как P = F = fN = fmg, то A = fmg |
|
5. Найти численное значение работы силы |
A = 0,4*45*9,81*5 = 882,9 Дж |
Аналогично для формирования других действий метода составляются соответствующие задания.
После того как каждое действие рассматриваемого метода сформировано при изучении конкретных тем, можно приступать к обучению студентов решению задач энергетическим методом, т.е. перейти ко второму подготовительному этапу. Для этого нужны определенные дидактические средства, а именно задачи, которые можно решать с применением энергетических понятий, закона сохранения и изменения энергии. При этом содержания задач должны быть практически значимыми для студентов. Это достигается путем специального подбора и разработки задач, в которых описаны ситуации, с которыми человеку приходится встречаться в быту или в профессиональной деятельности. Данные задачи преподаватель может подготовить в печатном варианте и раздать студентам или представить на слайдах в виде презентации. Приведем примеры таких задач:
1. Для эвакуации людей из совершившего аварийную посадку самолёта используется аварийный надувной трап, расположенный под углом 45 ° к поверхности земли. Начальная скорость человека равна нулю. Верхняя часть трапа находится на высоте Н = 3 м. Коэффициент трения µ = 0,2. Найти скорость, которую будет иметь человек в результате движения по трапу перед касанием о землю, и сравнить ее с условно безопасной скоростью v0 = 5 м/с.
2. Самолёт, пролетая над лагерем археологов, сбросил груз массой m = 50 кг с высоты h = 1500 м с начальной скоростью v0 = 25 м/с. Насколько углубится груз в грунт, если сила сопротивления грунта F = 90,6 кН?
3. Американские горки – опасный аттракцион, предоставленный искателям острых ощущений еще в 1890-x гг. Официальные источники утверждают, что первая «мёртвая петля» появилась в аттракционе Атлантик-Сити и работала вплоть до 1912 г., когда была закрыта из-за большой смертности посетителей. Для того, чтобы посетители смогли безопасно посещать аттракцион, необходимо, чтобы сила, прижимающая вагонетки к рельсам, превышала силу тяжести, действующую на состав. Определите начальную скорость, с которой состав должен войти на рельсы, чтобы повысить безопасность аттракциона, если длина поезда много меньше длины рельсов в «петле».
4. В спортивном плавательном центре каждая последняя среда месяца – санитарный день. В этот день проводятся механическая, химическая чистка воды, дезинфекция помещения ультрафиолетовым излучением, а также профилактическая чистка сливных труб. Для совершения работ необходимо пропустить в трубу тонкий длинный канат. С какой минимальной скоростью должен двигаться канат на горизонтальном участке трубы, чтобы пройти через кольцевую петлю радиуса r, если длина каната больше длины окружности, образованной петлёй в воздухе?
5. Нить длиной 2 м отклонена на угол α0 = arccos 3/4 от вертикали и привязанному к ней грузу сообщена начальная скорость 3,13 м/с. Найти наибольший угол отклонения нити в другую сторону от вертикали.
6. Во время пожара человек выпрыгнул с высоты 15 м в сугроб рыхлого снега. Глубина вмятины в сугробе оказалась равной 1 м. Найти скорость человека в момент касания сугроба. Сопротивление воздуха не учитывать.
Преподаватель предлагает рассмотреть первую задачу и разработать способ её решения. Далее, анализируя предложенные варианты решения, студенты совместно с преподавателем выделяют действия метода и фиксируют его в тетрадях. Таким образом, у обучающихся накапливаются способы решения конкретных физических задач с применением закона сохранения энергии. На этом этапе преподаватель проводит практические занятия по решению задач, акцентируя внимание студентов на каждом действии метода. Обучаемые фиксируют метод решения задач в тетрадях.
Приведем пример решения первой задачи энергетическим методом.
Нить длиной l = 2 м отклонена на угол α0 = arcos 3/4 от вертикали и привязанному к ней грузу сообщена начальная скорость v0 = 3,13 м/с. Найти наибольший угол отклонения нити в другую сторону от вертикали [8].
1. Выбрать первое и второе состояние тела на графической модели ситуации (рисунок).
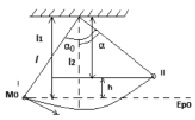
Графическая модель ситуации
За первое состояние груза примем положение, когда тело отклонили на угол α0, за второе состояние тела – максимальное отклонение груза от положения равновесия.
2. За нулевой уровень потенциальной энергии примем линию, проходящую через начальное положение тела.
3. Найдем кинетическую и потенциальную энергию груза в первом состоянии тела:
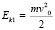 ,
, 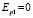 .
.
4. Найдем кинетическую и потенциальную энергию груза во втором состоянии тела:
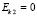 ,
, 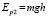 .
.
5. Найдем изменение энергии:
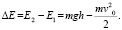
6. Данная система тел является замкнутой, поэтому 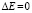 , тогда
, тогда
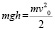 ,
,
следовательно,
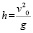 .
.
7. Найдем искомую величину:
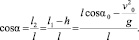
Вычислим 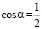 , тогда α ° = 60 °.
, тогда α ° = 60 °.
Далее, на третьем, методологическом этапе студенты, анализируя методы решения конкретных физических задач на закон сохранения изменения энергии, выделяют метод в обобщенном виде.
Последним этапом является самостоятельное решение физических задач из курса теоретической физики с применением энергетического метода.
Выводы
В результате организации такой работы с обучающимися у них формируется собственный опыт деятельности по применению знаний, приводящий к их неформальному усвоению, а также стиль мышления инженера, способного решать любые профессиональные проблемы.
Библиографическая ссылка
Крутова И.А., Исмухамбетова А.С., Дергунова О.Ю. ФОРМИРОВАНИЕ У СТУДЕНТОВ УНИВЕРСИТЕТОВ ЭНЕРГЕТИЧЕСКОГО МЕТОДА РЕШЕНИЯ ЗАДАЧ ПРИ ИЗУЧЕНИИ ДИСЦИПЛИНЫ «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА» // Современные наукоемкие технологии. 2017. № 7. С. 119-123;URL: https://top-technologies.ru/ru/article/view?id=36741 (дата обращения: 05.03.2026).