В современных системах телекоммуникаций [1, 2] все больший интерес представляет передача данных в параллельном формате данных, представленных в параллельной математике, такой как система остаточных классов (СОК) [3–5].
Изначально представление данных в таком формате позволяет существенно (в разы) увеличить скорость обработки данных, так как позволяет осуществлять операции сложения, вычитания и умножения без учетов переноса в разрядах, в отличие от позиционной системы исчисления (ПСС). Возникает задача передачи таких данных по существующим и перспективным каналам связи [6].
То есть данные представляются не некоторым числом Ai, а результатом его деления на взаимно простые заранее известные числа (основания) pi. То есть число представляется совокупностью вычетов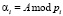 
или набором длины N вычетов 
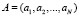. При этом операции сложения и умножения могут осуществиться параллельно независимо друг от друга по всем i основаниям, т.е. суммирование чисел А и В будет иметь вид 
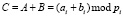и умножение 
.
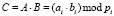СОК обладает естественной избыточностью, что позволяет помимо ускорения процедуры обработки данных существенно повысить надежность систем телекоммуникаций. Так как каждый вычет несет часть информации в себе о сигнале в целом, то можно говорить о возможности повышения надежности за счет возможности деградации структуры сети и снижения точности расчетов. Частным случаем такой передачи данных можно считать дельта-модуляцию.
При моделировании и построении каналов связи (КС) прежде всего, необходимо учитывать вероятностные характеристики источника сообщения. Очевидно, что в этом случае вычеты, имеющие различные абсолютные значения, будут иметь различную вероятность появления. Или различные законы распределения вероятностей вычетов по каждому основанию или впоследствии в отдельных подканалах. Именно вероятностное описание источника сообщения определяет модель КС. От этого будут зависеть переходные вероятности в подканалах, оптимальные пороги решающих схем и в конечном результате функциональные схемы реализации оптимальных решающих устройств. Также одной из проблем передачи данных в формате СОК по последовательным КС является обеспечение их эффективного помехоустойчивого кодирования. Также при проектировании параллельных КС для передачи параллельных данных отсутствует научно обоснованный подход к выбору полосы пропускания, типу линии выделяемой отдельному подканалу и др. параметров КС, определяемых вероятностными характеристиками. Кроме того, информационные характеристики определяются его вероятностными характеристиками. Очевидно, что отсутствие таких закономерностей сдерживает развитие параллельных КС в СОК. Таким образом, целью статьи является определение законов распределения вероятностей вычетов в системе остаточных классов.
Определим вероятность передачи вычета αi = pi – 1 по основанию pi в СОК при условии, что исходные данные в ПСС имеют равномерное распределение вероятностей.
Для любой системы вычетов максимальное значение вычета будет определяться максимальным же значением основания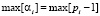 
. Возможна передача всех значений от 1 до 
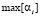. Вероятность передачи одного из вычетов αi по основанию pi с учетом нуля будет определяться как [6]
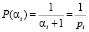. (1)
Для передачи всего числового диапазона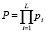 
необходимо передать все αi вычеты, где i = 1,…, L, L – число оснований, по всем основаниям. В общем случае число задействованных оснований для представления числа может быть меньше числа оснований системы СОК или N ≤ L. Тогда общая вероятность передачи определенного вычета по всем основаниям будет складываться из вероятностей его передачи по каждому из оснований.
Так вычет αi = 0 может быть передан по любому основанию, поскольку 0 является элементом каждого класса вычета. Вычет αi = c может быть передан только по основаниям pi > c. Согласно формуле полной вероятности вероятность передачи вычета αi во всем блоке данных должна определяться согласно формуле полной вероятности [7] его передачи по всем L основаниям
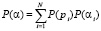, (2)
где N – число передаваемых вычетов в блоке данных, P(pi) – вероятность передачи любого вычета по основанию pi, то есть вероятность использования pi основания, P(αi) – вероятность передачи αi вычета по основанию pi. Если использовать равномерную передачу, при которой в блоке данных передаются вычеты по каждому основанию один раз N = L, то P(pi) можно считать равномерным и определить, как
P(pi) = 1/L. (3)
Если при этом блок передаваемых данных содержит вычеты по всем основаниям N = L, а распределение передаваемых значений равномерно, то подстановка выражений (3) и (1) в выражение (2) дает
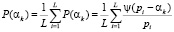, (4)
где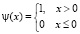 
модифицирования кусочно-постоянная функция Хевисайда, функция учитывающая тот факт, что вероятность передачи вычета αi по основанию pi ≤ αi будет равна 0. Так согласно (3) вероятность передачи 0 будет равна
.
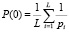На основании изложенного можно сформулировать теорему:
Перевод последовательного алфавита с равномерным распределением элементов из ПСС в СОК с последовательной передачей вычетов приводит к неравномерному и взаимозависимому распределению вычетов, причем закон распределения вероятностей по вычетам имеет вид (4).
Докажем данную теорему. Первое утверждение теоремы очевидно. Каждый элемент алфавита в ПСС должен быть представлен по всем основаниям набором вычетов, поэтому после записи вычета по старшему основанию обязательно следует вычет по младшему основанию, если нет дополнительного правила перемежения вычетов по псевдослучайному закону. Такая строгая последовательность означает наличие статистической взаимосвязи между элементами. Так же очевидно, что минимальные вычеты являются элементами множества вычетов по всем основаниям, в то время как максимальные вычеты являются элементами множества вычетов только по максимальным основаниям, т.е.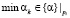 
, 
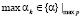. Таким образом, имеет место неравномерность распределения вычетов.
Вторая часть теоремы частично представлена при выводе выражения (4). Остается показать, что данное выражение удовлетворяет условию единичной нормировки, т.е. равенству 1 суммы вероятностей полной группы событий.
Пусть αk = k, тогда заметим, что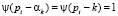 
только при условии k ≤ pi. Легко показать, что
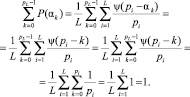
Теорема доказана.
Рассмотрим пример, так для оснований pi = 2, 3, 5, т. е. для L = 3 согласно (4) получим
.
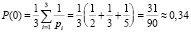То есть каждый третий вычет будет иметь значение равное 0. Заметим, что вычет αi = 1 является также элементом каждого класса вычетов по любым основаниям. То есть P(0) = P(1). Тогда в каждой тройке переданных вычетов два из них будут 1 или 0. Определим вероятность передачи остальных вычетов α = 2. Согласно (4)
,
,
.
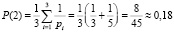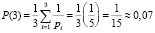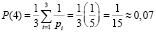Сумма вероятностей передачи вычетов P(0) + P(1) + P(2) + P(3) + P(4) = 0,34 + 0,34 + 0,18 + 0,07 + 0,07 = 1, поскольку она составляет полную группу событий.
Очевидно, что для максимальных вычетов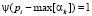 
только для i = L. Тогда согласно (4) вероятность появления максимальных вычетов
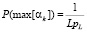, (5)
где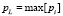 
– максимальное основание.
Рассмотрим взаимозависимую передачу вычетов. Будем считать последовательность передачи вычетов простейшим Марковским процессом, когда условное распределение последующего состояния зависит только от текущего состояния и не зависит от всех предыдущих состояний последовательности. Пусть вычеты передаются последовательно от меньшего основания к большему основанию. Тогда если передан максимальный вычет с вероятностью согласно (5)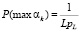 
, то следующий вычет будет только минимальным (или 0 или 1) и передан с условной вероятностью 
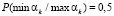. То есть вероятность передачи пары наибольшего и наименьшего вычетов составит
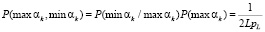. (6)
При последовательной передаче вычетов вероятность передачи максимального вычета после максимального будет равна 0, т.е.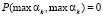 
. Так как по каждому основанию может быть передан минимальный вычет, то условная вероятность 
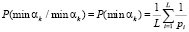, а вероятность, того, что после минимального вычета будет минимальный вычет, равна
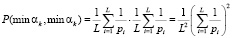. (7)
Аналогично с учетом того, что вероятность передачи одного из максимальных вычетов не изменится при передаче одного из минимальных вычетов, так как минимальные вычеты могут быть переданы по любому основанию, следовательно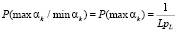 
, и вероятность передачи пары минимального и максимального вычетов будет равна
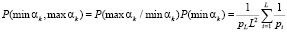. (8)
Выражения (6–8) позволяют рассчитать вероятности появления пар вычетов в последовательной передаче данных в формате СОК.
Анализ проведенных вычислений показывает, что чаще передаются вычеты 0 и 1. Следовательно, при передаче по каналам связи их необходимо кодировать более помехоустойчивым кодом. Однако необходимо помнить, вычеты большего абсолютного значения более важны при переводе данных из СОК в ПСС.
Другим важным выводом является тот факт, что для передачи данных в формате СОК целесообразно использовать асинхронные форматы передачи данных, так как резервирование временного окна при временном уплотнении TDMA подканалов в параллельном КС для передачи всего диапазона вычетов αi = 1… pi – 1 нецелесообразно, поскольку вычеты с меньшим значением передаются гораздо чаще.
Для устранения статистической зависимости между вычетами, приводящей к снижению информационной производительности источника сообщения, целесообразно использовать дополнительное статистическое кодирование, повышающее энтропию источника сообщения [7].
В вычислительных системах с двоичной системой счисления используются протоколы, форматы данных, разрядность шин адреса и данных кратных числам 2i = 2, 4, 8, 16, 32 … Это обусловлено разрядностью операционных систем, а также длиной машинных слов и команд машинного кода Х86, кратных байту (8 бит)
Очевидно, для уменьшения информационных потерь и адаптации существующих КС к каналам с передачей данных в СОК необходимо использовать основания близкие к 2i, такими могут быть числа Мерсенна [3, 6] pi = 2i –1. Тогда выражение (4) примет вид
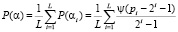. (9)
Например, для оснований pi = 3, 7, 31, однозначно представляющих диапазон чисел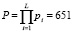 
без учета 0, необходимо передавать максимальный вычет 
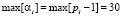. Вероятность передачи вычетов равных 0, 1 или 2 будет равна и составит
.
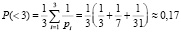То есть вероятность передачи 0, 1 и 2 составит P(0, 1, 2) ≈ 3•0,17 = 0,51 или каждый второй переданный вычет равен 0, 1 или 2. Таким образом, на остальные вычеты приходится вероятность P(3…30) = 1 – 3•0,17 = 0,49.
Анализ выражений позволяет сделать выводы:
1. Полученное выражение (4) позволяет оценить неравномерное распределение вычетов в системе остаточных классов при переводе, источник сообщений с равномерным законом распределения алфавита в позиционной системе исчисления.
2. Полученные выражения (5–8) позволяют учесть вероятность распределения вычетов при их последовательной передаче с учетом марковской взаимосвязи. Данные выражения можно учесть при построении функциональных схем оптимальных приемников.
3. Выражения (4–9) необходимо учитывать при оптимальном помехоустойчивом кодировании данных в различных каналах связи [8].
4. На основе полученных выражений можно делать практические рекомендации построения алгоритмов деградации вычислительных структур с потерей точности вычислений, но сохранении работоспособности канала связи.
5. Аналитическое выражение (9) учитывает возможную максимальную адаптацию к существующим двоичным каналам связи. При этом в качестве оснований используются ближайшие к 2i взаимно простые вычеты.
Таким образом, аналитические выражения (2–9) позволяют разрабатывать модели каналов связи при передаче данных в СОК. В дальнейшем на их основе необходимо развить теорию информации для данных, представленных в СОК. Знание законов распределения позволит оценивать такие параметры канала связи, как пропускная способность, скорость передачи информации, а также показателей качества, таких как помехоустойчивость, достоверность и др. показателей [7, 9]. Выражения (4–9) позволят проводить обоснованное статистическое моделирование КС при передаче данных в СОК, адаптировать существующие КС к передаче данных в СОК.
Библиографическая ссылка
Смирнов А.А., Саиег Т.Х., Даржания А.Д., Роженко О.Д., Смирнова О.Н. РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ ВЫЧЕТОВ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ // Современные наукоемкие технологии. – 2017. – № 7. – С. 78-82;URL: https://top-technologies.ru/ru/article/view?id=36733 (дата обращения: 21.11.2024).