Существует широкий класс технологических систем, включающих вторичное использование производимых гуммированных и некоторых металлических изделий.
Моделирование таких систем осложняется их физической и геометрической нелинейностью, а также сложностью описания взаимодействия с внешней средой. На примере производства гуммированных валов металлургических производств рассмотрим некоторые принципы системного моделирования. К настоящему времени разработаны некоторые математические модели элементов конструкций металлургических машин, технологических процессов получения смесей, резин. Однако и они не могут дать полного решения задачи оптимального конструирования и построения технологических процессов ввиду отсутствия единого целевого назначения. Перспективным подходом к решению проблемы является системное моделирование: создание системы моделей единого целевого назначения, позволяющих оценивать основные технико-экономические характеристики материалов и технологий резинометаллических изделий в различных условиях их функционирования путем вычислительного эксперимента. Альтернативы такому пути в современных условиях, по-видимому, нет, так как натурные эксперименты длительны, дороги, а зачастую просто неосуществимы. Только с помощью прикладной математики, которая на современном этапе переходит к непосредственному моделированию, а следовательно, прогнозированию и оптимизации разнообразных и сложных процессов, явлений, технических систем и управлению ими, можно решить данную проблему [1].
Анализ полного цикла функционирования резинометаллических изделий от их изготовления до вторичного использования приводит к необходимости построения единой иерархической, многоуровневой системы моделей с использованием разнообразного математического аппарата. При построении такой системы, описываемой N функциями {хj} при наложенных на нее М связях Сj(х), включающих L параметров, т.е. имеющих N – M + L степеней свободы, необходимо достижение моделью достаточной близости к системе по числу отображаемых параметров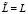 
. Это позволяет при задании целевого функционала 
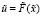искать оптимальное решение, близкое к экстремуму системы 
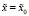, не стремясь при этом к приближению размерности модели 
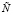к размерности системы N. Однако в применении к гуммированным конструкциям создание одной общей математической модели привело бы к значительному ее упрощению ввиду сложности объекта и ограниченности вычислительных возможностей, снижающих достоверность получаемых оптимальных оценок и затрудняющих одновременную оценку многих качеств системы.
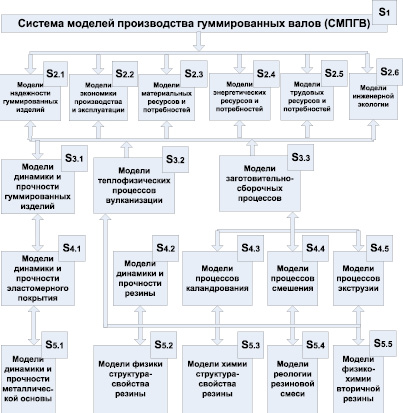
Рис. 1. Система моделей производства гуммированных валов (СМПГВ)
Рассмотрим систему моделей производства гуммированных валов (СМПГВ) металлургических производств в виде некоторого множества моделей (рис. 1):
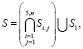
где S1 – модель внешнего описания; S2.j – множество моделей надежности гуммированных валов, экономико-материальных, энергетических и трудовых ресурсов инженерной экологии; S3.j – множество моделей динамики и прочности гуммированных изделий, теплофизических и заготовительно-сборочных процессов; S4.j – множество моделей динамики и прочности, резины и процессов ее производства; S5.j – множество моделей динамики и прочности металлической основы, физики, химии и реологии резины.
При этом каждое подмножество (Si.j) характеризуется своей размерностью, связями и числом параметров.
Система моделей представляет собой совокупность сложных древовидных структур, допускающих передачу информации как последовательно по уровням, так и за счет непосредственных связей между ними.
Целью каждого из подмножеств моделей является построение оптимальных (в общесистемном смысле) структур или процессов функционирования элементов. Если определять целевые функционалы каждого из подмножеств моделей на основе общей цели системы, описываемой с помощью закона потенциальной эффективности, то в вычислительном плане такой подход разбиения на некоторое множество моделей позволит в целом приблизить общую систему по размерности к реальной системе.
Рассмотрим СМПГВ металлургических производств [2, 3]. Система (А), взаимодействуя со средой (В), потребляет сырьевые, энергетические, трудовые и другие ресурсы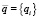 
, отдавая ей их часть 
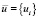в виде изношенных покрытий валов, отходов производства, рассеиваемой энергии и т.д. Обеспечивая свою надежность, система находится в непрерывном 
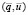-обмене со средой.
Основная цель СМПГВ – минимизация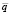 
при обеспечении необходимого суммарного ресурса валов в эксплуатации. Таким образом, стоит задача построения системы с оптимальным 
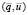-обменом:
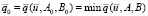
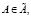
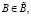
где A0 и B0 – СМПГВ и среда, оптимальные в соответствующих множествах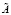 
и 
.
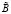Так как воздействие среды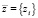 
носит случайный характер, то можно говорить только о вероятности 
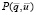существования данного 
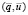-обмена. А вероятность оптимального обмена 
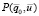является потенциальной эффективностью системы. В этих условиях особую важность приобретает фактор надежности системы, то есть способности сохранения показателей в заданных пределах в течение длительного времени.
В каждой отдельной модели проявлением общесистемных «интересов» является замена безусловного функционала при поиске оптимума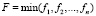 
на условный, ограничения которого и являются отражением целенаправленности системы:
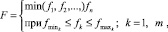
где fi – параметры модели; fmink и fmaxk – условия, накладываемые на параметры модели.
Таким образом, приближение каждого подмножества моделей к своему оптимуму при достаточной близости к объему по размерности в подмножестве повышает эффективность оценок СМПГВ.
Рассмотрим подробнее наиболее разработанные модели S1, S2.1, S3.1. Каждый уровень имеет свою структуру, представленную одной или несколькими моделями. При движении по уровням сверху вниз уменьшается количество связей с внешней средой, что вызывает и соответствующие изменения в применяемом математическом аппарате.
Внешнее описание СМПГВ (S1) предназначено для поиска оптимальных путей развития системы с учётом параметров среды и стратегии системы. Модель построена исходя из принципа неразрывности и связности расходуемых и потребляемых ресурсов:
,
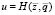где Н – нелинейный оператор.
Для количественной оценки потенциальной эффективности СМПГВ предложено выражение потенциальной функции
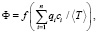
где qi – объемы потреблении различных ресурсов, таких как новая резина, адгезивы (клеи), металлическая основа, трудовые и энергетические затраты и т.д.; ci – стоимостные показатели соответствующих qi; n – число учитываемых видов ресурсов; <Т> – суммарный необходимый ресурс гуммированного вала в эксплуатации.
Для вычисления Ф строится система уравнений равновесия, основанных на потенциальной функции неразрывности потоков соответствующих ресурсов.
С помощью описываемой модели проводили анализ существующих и перспективных технологий производства гуммированных валов металлургического оборудования. Было показано, что наиболее весомыми параметрами, определяющими эффективность СМПГВ, являются полный ресурс гуммированных валов. При решении задачи выбора оптимальных параметров валов для получения максимального полного ресурса используется одна из моделей второго уровня.
Модель надежности гуммированных изделий (S2.1), как и другие модели внутреннего описания СМПГВ, предназначена для целенаправленного изучения ряда аспектов функционирования системы. Рассматриваются зависимость полного ресурса валов от конструктивных параметров эластомерной обкладки (толщина слоев всей обкладки, число слоев и т.д.) и прогнозирование ресурса валов в эксплуатации. Модель включает следующие основные этапы [4]:
- расчет по результатам эксплуатационных испытаний функций вероятности безотказной работы базовой модели вала по отдельным отказам в эксплуатации и по совокупности отказов;
- определение влияния вносимых конструктивных, материаловедческих, технологических изменений в проектируемой эластомерной обкладке по сравнению с базовой моделью;
- расчет функций вероятности безотказной работы проектируемого вала;
- определение показателей доремонтного, послеремонтного и полного ресурсов;
- определение оптимальных конструктивных параметров эластомерного покрытия, обеспечивающих при заданных требованиях долговечности наименьшие затраты на производство, воспроизводство и эксплуатацию валов.
Модели динамики и прочности гуммированных изделий (S3.1) изучают покрытие вала с целью оценки его прочности и долговечности, прогнозирования характеристик на стадии проектирования.
Все имитационные модели, описывающие аспекты создания и применения гуммированного вала, можно классифицировать в соответствии со схемой (рис. 2). В моделях конструирования формализованы концепции создания и оптимизации гуммированного вала для заданных условий эксплуатации. Динамические модели взаимодействия вала с элементами агрегата и средой изучают условия нагружения вала при эксплуатации и влияние его выходных характеристик на поведение системы. Моделирование «внешней» механики гуммированного вала на основе данных о его структуре и материалах проводится с целью определения и оптимизации выходных характеристик, таких как радиальная скорость движения, критическая скорость, параметры контакта с элементами агрегата, рассеивание энергии в стационарных условиях.
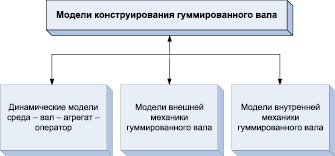
Рис. 2. Структура моделей динамики и прочности гуммированного вала
Ограничения, накладываемые на выходные характеристики, формулируются в ходе моделирования системы на более «высоких» уровнях и формализации требований руководящих документов (ГОСТы, СТП, РД). Характерным примером служит модель «кольца» на упругом основании с упругой обкладкой, используемая для определения критической скорости, радиальной жесткости вала и других параметров [3].
В качестве примера системного взаимодействия имитационных моделей рассмотрим подсистему моделей конструкционной прочности обкладки (рис. 3). Конструкционная прочность обкладки определяется усталостной долговечностью материала и прочностью связи резины на границах элементов конструкции, поэтому задачей подсистемы является квазидинамический расчет элементов конструкции гуммировочного покрытия. На первом этапе модель S3.1.1 изучает динамическую систему вал – обкладка – агрегат – оператор. Основная цель этого этапа – конкретизация воздействий среды, т.е. эксплуатационных условий узла, агрегата и т.п. (эксплуатационные внешние воздействия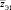 
) в виде статистических параметров нагрузки 
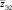на вал в этих условиях.
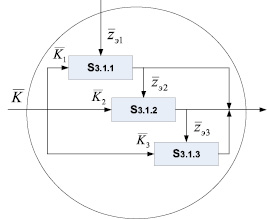
Рис. 3. Подсистема моделей конструкционной прочности обкладки: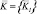 
– параметры конструкции; zэ.i – внешние воздействия для каждой из моделей
Решение поставленной задачи складывается из результатов моделирования вала с покрытием по трем группам моделей, соответствующих нагружению вала при вертикальных и боковых колебаниях, а также по нагружению в тягово-тормозном режиме [4]. Необходимость разбиения процесса нагружения вала на различные аспекты связана со сложностью задачи. Наиболее полно разработаны математический аппарат и модели для анализа вертикальных колебаний. Эта задача решается методом статистического моделирования, что, с одной стороны, хорошо согласуется с известными методами описания, а с другой – не требует линеаризации параметров системы [5]. В результате моделирования определяют статистические и частотные параметры нагрузок на вал и распределение потерь механической энергии в системе. Применяемая модель вала отражает наиболее важные и характерные черты объекта. Этот уровень моделирования позволяет проследить влияние изменения любых параметров системы вал – обкладка – агрегат – оператор на ее поведение, что при натурном эксперименте бывает затруднительно из-за необходимости большого объема испытаний или невозможно по техническим причинам.
Модель S3.1.2 позволяет для условий статического нагружения провести расчет перемещений и напряженно-деформированного состояния (н.д.с.) ряда элементов вала при различных внешних нагрузках. Используя результаты расчетов по этой модели на нижнем уровне (модель S3.1.3), представляющем трехмерную задачу теории упругости, которая решается методом конечных элементов, исследуют н.д.с. в элементах металлической основы со сложной структурой.
С учетом результатов статического расчета н.д.с. для дискретного спектра нагрузок и статистической информации о распределении нагрузок в динамике определяют н.д.с, эквивалентное сложному нагружению в заданных условиях эксплуатации, что в целом реализует квазидинамическую модель.
Таким образом, дальнейшее исследование технико-экономических проблем производства и функционирования резинометаллических валов, а также поиск оптимальных решений в этой области связаны с сочетанием имитационных и оптимизационных моделей. Полагаем, что системное моделирование подразумевает использование комплекса моделей разного типа и разной сложности, позволяющее оценивать разнообразные параметры системы. Такой подход дает возможность уже сегодня применять высокоэффективный системологический аппарат в решении задач металлургической промышленности.
Библиографическая ссылка
Осипов С.Ю., Осипов Ю.Р., Богданов Д.А., Шлыков С.А. СИСТЕМНОЕ МОДЕЛИРОВАНИЕ ПОЛНОГО ЦИКЛА ФУНКЦИОНИРОВАНИЯ ОБЪЕКТОВ С ЭЛАСТОМЕРНЫМИ ПОКРЫТИЯМИ // Современные наукоемкие технологии. – 2017. – № 7. – С. 49-54;URL: https://top-technologies.ru/ru/article/view?id=36728 (дата обращения: 21.11.2024).