Основной задачей математического моделирования транспортных перевозок является построение оптимального плана перевозок [1]. В классической постановке Монж – Канторовича предполагается оптимизация по времени или стоимости перевозок однородного груза без учета временных требований заказчика, то есть требований выполнения сроков поставок. Это серьезное допущение значительно сужает возможности использования классической транспортной задачи при решении прикладных вопросов. В данной работе предлагается обобщение математической модели транспортных перевозок с учетом времени поставок.
Классическая транспортная задача
Математическая постановка классической транспортной задачи сводится к следующему [2–4]: требуется найти минимум линейной формы с n + m переменными:
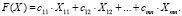 (1)
(1)
С выполнением баланса по поставкам от m поставщиков
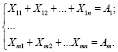
С выполнением баланса по заказам от n заказчиков
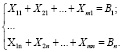
Очевидно, принимается, что Xij ≥ 0.
Коэффициенты cij линейной формы (1) определяют стоимость или время перевозки единицы груза от i-го поставщика к j-му заказчику; Xij – количество груза, отправляемое от i-го поставщика к j-му заказчику.
Одним из видов транспортных задач является так называемая транспортная задача в замкнутой форме – суммарные объемы поставок и заказов равны. Замкнутая транспортная задача в классической ее постановке решается методом потенциалов, который достаточно полно изложен в работах [3, 6].
Транспортная задача с учетом времени поставок
В данной работе в замкнутую транспортную задачу вводятся два типа дополнительных ограничений. Одни дополнительные ограничения связаны с выполнением всех поставок в заданный срок, то есть у каждого заказчика есть определенный срок, к которому необходимый ему груз должен быть доставлен.
Другие дополнительные ограничения связаны со скоростью поставки от поставщика к заказчику, то есть у каждого поставщика есть определенные технологические ограничения, вследствие которых он не может доставить груз быстрее.
Каждый из n заказчиков задает сроки поставок, которые формируют вектор сроков поставок:
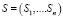 .
.
Каждый из m поставщиков задает скорости поставок от i-го поставщика к j-му заказчику, которые формируют матрицу скоростей поставок:
 .
.
Элемент матрицы поставок vij задает возможный объем вывозимых грузов от i-го поставщика к j-му заказчику в единицу времени.
Для того, чтобы каждый i-ый поставщик мог бы в срок не более чем за Sj единиц времени поставить свой груз в размере Xij, j-му заказчику требуются следующие дополнительные m + n×ограничений по скоростям поставок:
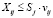 . (2)
. (2)
Это первое дополнительное ограничение.
В то же время скорости поставок должны быть такими, чтобы не позже назначенного заказчиком срока Sj, заказы в объемах Bj должны быть выполнены. Таким образом, получаем второе дополнительное ограничение, связывающее сроки и скорости поставок:
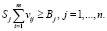 (3)
(3)
кроме этого, необходимо обеспечить вывоз всех объемов поставок, что приводит ко второму условию на сроки заказов и скорости поставок:
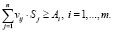 (4)
(4)
Условия (3, 4) являются условиями разрешимости транспортной задачи с учетом времени поставок. Напомним, что условием разрешимости классической транспортной задачи является условие замкнутости [2, 4].
Таким образом, сформулированная транспортная задача с учетом времени поставок обобщает классическую транспортную задачу и формулируется следующим образом.
Требуется найти минимум линейной формы (1) с ограничениями (2, 3, 4):
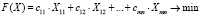 ,
,
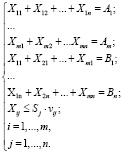
Модель транспортной задачи при введении дополнительных условий можно использовать для оптимизации процесса перевозок, учитывая основное требование, а именно: выполнение всех поставок в заданный срок. Приведенная транспортная задача с учетом времени поставок решается симплекс-методом.
Результаты исследования и их обсуждение
Рассмотрим примеры решения классической транспортной задачи и транспортной задачи с учетом времени поставок.
Классическая транспортная задача. Имеется три поставщика с заданными запасами товаров:
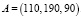
и четыре заказчика с соответствующими потребностями:
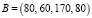 .
.
Матрица тарифов имеет вид
 .
.
Модель транспортной задачи является замкнутой.
Математическая модель данной транспортной задачи имеет вид: требуется найти минимум следующей линейной формы:
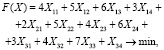
при условии Xij ≥ 0 и следующих ограничениях:
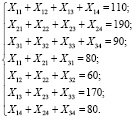
Задача решалась методом потенциалов. Решение имеет вид
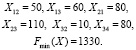
Транспортная задача с учетом времени поставок. В условия предыдущего примера добавим вектор сроков поставок:
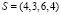 ,
,
и матрицу скоростей поставок:
 .
.
Легко установить, что необходимые условия разрешимости задачи (3, 4) выполняются.
Дополнительные двенадцать ограничений по срокам поставок (2) имеют следующий вид:
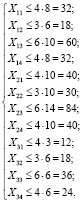
Переобозначим переменные в целевой функции (1) и в ограничениях (2, 3, 4).
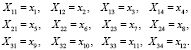
Получим следующую математическую постановку задачи в новых обозначениях.
Найти минимум линейной формы:
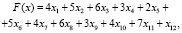
при ограничениях
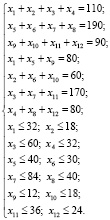
Задача решена симплекс-методом. Решение имеет вид
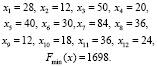
Наглядное сравнение решений классической транспортной задачи и транспортной задачи с учетом времени поставок приведено в таблице.
Сравнение решений классической транспортной задачи и транспортной задачи с учетом времени поставок
|
Без ограничения сроков поставок |
С ограничением сроков поставок |
||||||||||
|
1 |
2 |
3 |
4 |
Запасы |
1 |
2 |
3 |
4 |
Запасы |
||
|
1 |
0 |
50 |
60 |
0 |
110 |
1 |
28 |
12 |
50 |
20 |
110 |
|
2 |
80 |
0 |
110 |
0 |
190 |
2 |
40 |
30 |
84 |
36 |
190 |
|
3 |
0 |
10 |
0 |
80 |
90 |
3 |
12 |
18 |
36 |
24 |
90 |
|
Потребности |
80 |
60 |
170 |
80 |
Потребности |
80 |
60 |
170 |
80 |
||
|
Fmin(x) = 1330 |
Fmin(x) = 1698 |
||||||||||
Отсюда видно, что учет времени поставок оказывает существенное влияние на оптимальное распределение поставок и значение минимума транспортных затрат.
Следует отметить, что с возрастанием скоростей поставок решение транспортной задачи с учетом времени поставок будет стремиться к решению классической транспортной задачи. В случае, когда правые части ограничения (4) будут не меньше потребностей соответствующего заказчика, эти ограничения будут автоматически выполнены и решения обеих задач совпадут. Если рассматриваемая транспортная задача является открытой, то необходимо ввести дополнительного заказчика с объемом заказов, делающих задачу замкнутой. Тарифы перевозок к этому заказчику задаются равными нулю, а время поставок к нему достаточно большим.
Учет времени поставок при моделировании транспортных перевозок позволит находить более адекватные оптимальные решения в задачах логистики [1], в транспортных задачах горной промышленности [7], металлургии [8], пищевой промышленности [9] и других областях.
Заключение
В статье описана транспортная задача, в которую введены дополнительные ограничения, связанные с выполнением всех поставок в заданный срок. Показано, что учет времени поставок оказывает существенное влияние на оптимальное распределение поставок и значение минимума транспортных затрат. Также отмечено, что с возрастанием скоростей поставок решение транспортной задачи с учетом времени поставок будет стремиться к решению классической транспортной задачи.
Библиографическая ссылка
Гоголин В.А., Николаева Е.А. ТРАНСПОРТНАЯ ЗАДАЧА С УЧЕТОМ ВРЕМЕНИ ПОСТАВОК // Современные наукоемкие технологии. 2017. № 7. С. 23-26;URL: https://top-technologies.ru/ru/article/view?id=36723 (дата обращения: 05.03.2026).



