Лазерная триангуляция в последнее время находит все большее применение при создании прецизионных измерительных датчиков и систем для решения широкого класса задач размерного контроля в диапазоне от единиц миллиметров до метра с погрешностями от долей микрона до сотен микрон.
Одной из задач, решаемой триангуляционными датчиками, является контроль за состоянием несущих конструкций плотин гидротехнических сооружений. Так как плотины являются объектами повышенной опасности, им требуется постоянный контроль. Наблюдения за состоянием гидротехнических сооружений представляют из себя контроль смещений тела плотины, который осуществляется измерением смещения контрольных точек вертикальных отвесов. Данные отвесы закладываются в конструкцию плотины на этапе строительства.
Несмотря на большое многообразие автоматических систем для визуального контроля, в настоящее время контрольно-измерительные задачи решаются при помощи визуальных измерителей, построенных по схеме Катырева – Брехмана [1]. Недостатками датчиков, построенных по схеме Катырева – Брехмана, являются большой вес и размеры, а также ошибки снятия отсчетов оператором и, как следствие, невысокая точность. На некоторых гидротехнических сооружениях для решения задач контроля используются фотоэлектрические преобразователи перемещения. Устройства, основанные на них, являются более точными, однако их стоимость высока.
Исходя из всего вышесказанного, вытекает необходимость создания мобильной контрольно-измерительной системы, с высокой точностью работы, с малыми габаритами, с возможностью обеспечить измерения в двух плоскостях, а также устройство должно быть простым в эксплуатации и иметь функцию быстрой настройки. Подобное устройство должно упростить контрольно-измерительные операции, проводимые на гидротехнических сооружениях, и повысить их точность [1].
Объект исследования
Объектом исследования является струна отвеса, несущих конструкций гидросооружений и устройство, основанное на триангуляционном методе. Триангуляция является одним из распространенных методов измерения расстояний до объекта в силу простоты реализации в оптико-электронных устройствах [1]. Триангуляционный метод измерения расстояния от контрольно-измерительной системы до поверхности объекта предполагает, что в оптическую схему датчика включен сам контролируемый объект – струна. Его характеристики (форма, характер поверхности и расположение относительно измерителя) могут существенно влиять на результаты триангуляционных измерений.
Принцип измерения заключается в том, что любое изменение положения струны вызывает соответствующее ему изменение положения светового пятна на фотоприёмнике. Зная параметры оптической системы, можно вывести формулу, связывающую изменение положения объекта с изменением положения светового пятна на фотоприёмнике. Это можно пояснить, используя рис. 1.
Лазерный луч осветителя 1 падает на поверхность струны 3. Отраженные от струны лучи, объективом 4 собираются на фотоприёмнике 5, который устанавливается под некоторым углом триангуляции α к осветителю так, чтобы осветитель, струна и блок фотоприёмника 2 образовали треугольник. В реальных триангуляционных системах эти лучи проецируются на многоэлементный фотоприёмник 5 [3]. В процессе смещения струны Δh происходит пропорциональное смещение её изображения Р на фотоприемнике, по которому судят о реальной величине смещении струны, а именно [5]
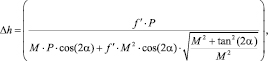(1)
где M – увеличение оптической системы; f’ – заднее фокусное расстояние системы.
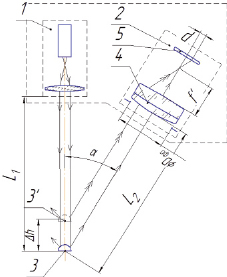
Рис. 1. Триангуляционный метод измерений: L1 – расстояние до нулевого положения струны; L2 – расстояние от струны до главной плоскости объектива фотоприемного узла; f’ – фокусное расстояние объектива; p – смещение светового пятна на ФП; Δh – смещение струны; α – угол триангуляции
Существуют два типа триангуляционных устройств: в первом случае плоскость устройства перпендикулярна его оптической оси, а во втором – наклонена к ней под определенным углом в соответствии с принципом Шеймпфлюга [4].
В зависимости от того, какими свойствами обладает поверхность струны, следует использовать разные схемы триангуляционного измерения [2]. При работе со струной можно использовать любую из схем, т.к. с одной стороны струна хорошо отражает падающее на нее излучение, а с другой – из-за круглой (в сечении) формы и наличия шероховатости рассеивает падающий пучок света.
Принципиальная схема предлагаемого триангуляционного датчика приведена на рис. 2. Она содержит следующие компоненты: осветитель 1, объектив 2, фотоприёмник (ФП) 3.
Для того чтобы проектируемое устройство удовлетворяло условиям поставленной задачи, необходимо задать начальные параметры, рассчитать осветитель, объектив и выбрать фотоприёмник, а затем оценить рассчитанные значения.
Работоспособность контрольно-измерительной системы, в основе которой лежит триангуляционный метод измерения расстояния до объекта, сильно зависит от формы и размеров струны. Поэтому большое внимание следует уделить выбору пары осветитель – фотоприемник, так чтобы отношение сигнал/шум на фотоприёмнике, позволяло выделить полезный сигнал на фоне шумов. Также не стоит забывать, что помимо потерь, связанных с формой струны, остается еще ряд факторов, которые влияют на падающее излучение, к примеру потери на рассеивание и поглощение при прохождении воздушного тракта до струны и обратно.
Энергетический расчет в упрощенном виде можно провести исходя из допущений, что среда, в которой распространяется лазерное излучение, не вносит изменений ни в геометрию пучка, ни в его энергетику, а оптические компоненты свободны от аберраций. При этом потери обусловлены лишь формой и размером струны. В процессе реализации поставленной задачи оценку сигнал/шум можно свести к отношению площадей пучка лазерного излучения при различных положениях струны.
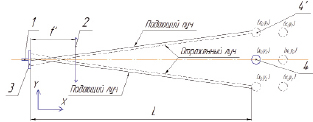
а
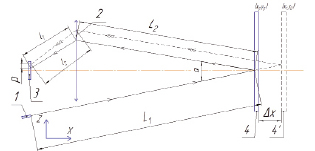
б
Рис. 2. Принципиальная схема триангуляционного контрольно-измерительного устройства: L1 – расстояние до нулевого положения струны; L2 – расстояние от струны до главной плоскости объектива фотоприемного узла; Δ – смещение струны; α – угол триангуляции; l1 и l2 – расстояние от главной плоскости объектива до фотоприемной площадки
Сечение пучка лучей, освещающего струну, представляет из себя эллипс, площадь S1 которого определяется по следующей известной формуле:
S1 = a1•b1•π, (2)
где а1 и b1 – малая и большая полуоси эллипса, рассчитываемые по формулам
а1 = d0 + L1•tan(φ1), (3)
b1 = d0 + L1•tan(φ2). (4)
В формулах (3) и (4) – d0 – диаметр пучка излучения на выходе из осветителя; L1 – расстояние от осветителя до струны; φ1 и φ2 – углы расходимости лазерного излучения.
Отраженное излучение от струны распространяется в широком телесном угле. В первом приближении можно положить, что отражение будет равномерным по всему диаметру струны. А при помощи коэффициента K можно рассчитать ту часть отраженного излучения, которая будет лежать в телесном угле, ограниченном входным зрачком объектива. Для расчета полного отражения от струны, которое определяется площадью S2 (рис. 3), воспользуемся следующей формулой:
S2 = Ka2 b2 π, (5)
где a2 – диаметр струны; b2 – размер светового пятна в продольном сечении струны, который высчитывается по следующей формуле:
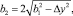(6)
где Δy – смещение струны относительно нулевой точки (рис. 3).
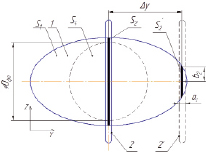
Рис. 3. Отношение площади сечения пучка излучения к площади струны: 1 – сечение пучка; 2 – струна в нулевом положении; 2’ – струна в крайнем положении
Коэффициент K, учитывающий изменение площади S2 на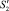 
, находится по формуле
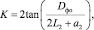(7)
которая легко выводится из анализа рис. 1.
Излучение осветителя, отраженное от струны, «срезается» еще раз на входе в блок фотоприёмника, дело в том, что входной диаметр объектива много меньше, чем сечение пучка излучения.
Излучение на входе в блок фотоприёмника будет определяться площадью S3 (в сечении тоже эллипс), которую можно рассчитать по формуле
S3 = a3 b3 π, (8)
где a3 и b3 – малая и большая полуоси эллипса на входе в блок фотоприёмника, рассчитываемые по формулам
a3 = 2(a2 K + L2 tan(φ1)); (9)
b3 = 2(b2 + L2 tan(φ2)). (10)
Для определения полного коэффициент потерь Kп необходимо определить площадь входного зрачка S4 объектива, роль которого выполняет первая оправа линзы. Нетрудно видеть, что она равна (рис. 3)
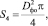(11)
тогда
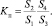(12)
Очевидно, что мощность излучения Pk, падающая на фотоприёмник, определяется как произведение мощности излучения осветителя Pн и коэффициента потерь Kп, т.е.
Pk = Pн Kп. (13)
Для проведения предварительных расчетов была взята схема, изображенная на рис. 2. Также были заданы начальные данные, представленные в табл. 1.
Данная система предназначена для автоматической регистрации смещений несущих конструкций гидротехнических объектов. По предложенному алгоритму был произведен энергетический расчет результаты представлены в табл. 2.
По произведенному расчету была выбрана следующая пара осветитель – фотодиод.
В качестве осветителя был выбран двух координатный PSD приемник DL100-7 SMD компании First sensor. В качестве осветителя был выбран лазерный модуль KLM-H808-x-5. Отношение сигнал/шум у данной пары 2,3•104.
Таблица 1
Начальные данные для предварительного расчета триангуляционной измерительной системы
|
Мощность осветителя Pн, мВт |
Рабочие расстояния, мм |
Диапазон измерений z, мм |
Диаметр струны а2, мм |
Диаметр выходного зрачка d0, мм |
Угол расходимости, град |
||
|
L1 |
L2 |
α1 |
α2 |
||||
|
4000 |
1000 |
950 |
–75...+75 |
2 |
5 |
9,6 |
9,6 |
Таблица 2
Результаты расчета триангуляционной измерительной системы
|
Мощность излучения на поверхности струны, мВт |
Мощность излучения, отраженная от струны, мВт |
Мощность излучения на фотоприемнике, мкВт |
|
4000 |
5,234 |
59 |
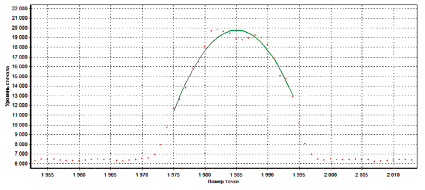
Рис. 4. Зависимость уровня сигнала на фотоприёмнике от положения струны. Точками изображен график, построенный по полученным экспериментальным данным, сплошной линией – аппроксимация экспериментальных данных
Заключение
Апробация разработанной методики проводилась на установке, описанной в [1], в которой были установлены указанные фотоприёмники и осветитель при заданных параметрах. При этом удавалось уверенно снимать и обрабатывать информацию с фотоприемника, даже не требовалось специально экранировать его, что является косвенным подтверждением того факта, что отношение сигнал/шум у этой пары существенно выше одного порядка. На рис. 4 приведен уровень сигнала, снимаемого с фотоприемника в зависимости от положения струны.
Более точные данные планируется получить на следующем этапе работы. Другим положительным моментом применения методики является возможность моделирования различных комбинаций фотоприемник\источник излучения и выбора оптимальной комбинации.
Библиографическая ссылка
Миннигазимов Р.И., Митрофанов С.С., Порохин В.В., Гнездилова М.С. РАЗРАБОТКА МЕТОДИКИ РАСЧЕТА ТРИАНГУЛЯЦИОННЫХ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ // Современные наукоемкие технологии. – 2017. – № 6. – С. 67-71;URL: https://top-technologies.ru/ru/article/view?id=36700 (дата обращения: 21.11.2024).