Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Рецензия
• Файлы
• Ключевые слова
• Литература

Костюк А.И. 1

---

1 ФГАОУ ВО «Южный федеральный университет»

Настоящая статья посвящена исследованию проблемы идентификации изображений. В данной работе предлагается изоморфно-статистический метод идентификации, который обладает свойством изоморфизма по отношению к поворотам распознаваемого изображения, что позволит снизить требования к предварительной обработке изображений. Предложенный метод идентификации изображений основан на представлении изображения в качестве двумерной интерпретации одномерного случайного процесса. Это также оценивание различных моментов, характеризующих обрабатываемое изображение, причем оценивание указанных моментов может производиться как непосредственно по имеющейся реализации изображения, так и с помощью предварительно полученной гистограммы. Были поставлены эксперименты над простыми фигурами, представленными бинарными изображениями, в результате которых были определены их числовые характеристики, необходимые для анализа геометрических особенностей с целью однозначной идентификации сравниваемых изображений.

Рецензия № 1

136 KB

Рецензия № 2

133 KB

Статья в формате PDF

0 KB

идентификация изображений

изоморфно-статистическая идентификация

числовые характеристики изображений

геометрические примитивы

распознавание образов

1. Мерков А.Б. Распознавание образов. Введение в методы статистического обучения. – М.: URSS, 2011. – 256 с.

2. Мерков А.Б. Распознавание образов. Построение и обучение вероятностных моделей. – М.: URSS, 2014. – 240 с.

3. Визильтер Ю.В. Обработка и анализ изображений в задачах машинного зрения / Ю.В. Визильтер, С.Ю. Желтов, А.В. Бондаренко, M.B. Ососков, А.В. Mopжин. – М.: Физматкнига, 2010. – 689 с.

4. Костюк А.И., Поленов М.Ю., Лукьянов В.А., Мунтян Е.Р. Модель централизованного управления в системе Smart House с использованием гипервизора // Известия ЮФУ. Технические науки. – 2014. – № 7 (156). – С. 170–177.

5. Мунтян Е.Р., Поленов М.Ю., Костюк А.И. О подходе к модернизации программной системы поддержки управленческих решений // Известия ЮФУ. Технические науки. – 2015. – № 3 (164). – С. 54–62.

6. Мунтян Е.Р., Поленов М.Ю., Kостюк А.И. Автоматизированная программная среда поддержки управленческих решений // Известия ЮФУ. Технические науки. – 2014. – № 6 (155). – С. 101–108.

В настоящее время известны как статистические, так и детерминированные методы идентификации изображений [1–3]. К недостаткам существующих детерминированных методик распознавания изображений можно отнести следующие:

• необходимость большого объема вычислений сравниваемых характеристик каждого из хранимых изображений с идентифицируемым;
• низкое быстродействие процесса идентификации изображений;
• недостаточно высокая помехозащищенность.

Как правило, использование детерминированной модели приводит к более простым техническим решениям. Однако детерминированная модель является частным случаем статистической, поэтому построение теории на основе статистической модели вполне оправдано [1].

Цель исследования

Необходимость статистической модели распознавания диктуется следующими условиями:

• большинство идентифицируемых объектов характеризуется случайной природой, например фотографии, написание рукописных букв и т.д.;
• идентификация происходит, как правило, в условиях помех, например нечеткость изображения, случайные вкрапления на фотографии;
• вероятностная идентификация позволяет проводить распознавание при наличии ошибок и позволяет оценить их количественно.

При этом предполагается наличие априорных сведений об идентифицируемых объектах. В противном случае можно говорить только о различении объектов или явлений по одному или нескольким признакам. Изучение общих свойств объектов необходимо для получения априорных сведений, необходимых при идентификации.

В случае имеющихся статистических методов идентификации недостатком является конечное количество распознаваемых классов (например, распознавание букв только определенного заданного алфавита), необходимость априорного задания вероятностей идентифицируемых классов и их признаков (например, заранее известная частота появления определенной буквы в тексте) [2, 3].

Таким образом, применение существующих статистических методов идентификации нецелесообразно, что и предопределяет необходимость разработки такого метода, который был бы свободен от указанных недостатков.

Материалы и методы исследования

Особенностью предлагаемого метода идентификации изображений является то, что идентифицируемые изображения интерпретируются как случайные процессы двух переменных. Таким образом, как и в случае анализа изображений, при статистической интерпретации дискретные изображения рассматриваются как реализации случайного поля, которому присущи те или иные вероятностные характеристики. В первую очередь это совместный двумерный закон распределения вероятностей, который позволяет теоретически рассчитывать корреляционные функции изображения [1].

Предложенный метод идентификации изображений основан на представлении изображения в качестве двумерной интерпретации одномерного случайного процесса, по данным которого и производится оценивание отдельных статистических характеристик. Изображения могут рассматриваться как реализации некоторого двумерного случайного поля, свойства которого априорно обычно неизвестны.

Применительно к анализу изображения ||Aij|| размером N_i×N_j элементов соответствующая формула вычисления начальных моментов mk k-го порядка приобретает вид

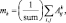(1)

где sum – количество обработанных пикселей исходного изображения.

Центральные моменты uk определяются выражением

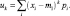(2)

Особо можно выделить такие характеристики, как

u2 – центральный момент второго порядка (дисперсия); (3)

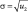– среднеквадратичное отклонение; (4)

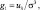(5)

здесь g1 – коэффициент асимметрии, характеризующий «скошенность» распределения вероятностей. Для симметричного (относительно математического ожидания) распределения коэффициент асимметрии равен нулю.

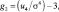(6)

здесь g2 – коэффициент эксцесса, характеризующий «крутость» распределения.

I – энтропия дискретной случайной величины, она же средняя собственная информация. Определяется известным из теории информации выражением

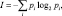(7)

где pi – как и ранее, вероятность, с которой случайная величина X принимает значение xi.

Рассмотрим определение числовых характеристик для бинарных нормированных изображений. Нормирование происходит следующим образом:

• производится центрирование изображения;
• изображение масштабируется таким образом, чтобы полностью заполнять окно анализа, причем коэффициенты масштабирования по осям одинаковы;
• выделяются контуры изображения;
• производится операция бинаризации полученного результата.

Как видно из формулы (1), для нормированных изображений в силу того, что значения X принимают только значения 0 либо 1, начальные моменты будут равны между собой, т.е. мы имеем

m1 = m2 = m3 = m4 = m,

где 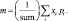(8)

Используя выражения (1), (2) и (8), преобразуем формулы расчетов центральных моментов:

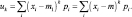(9)

Тогда применяя (3)–(7), окончательно получим следующий набор числовых характеристик изображения (10):

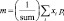– начальные моменты;

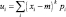– центральные моменты;

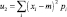– дисперсия;

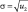– среднеквадратичное отклонение;

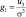– асимметрия;

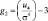– эксцесс;

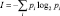– энтропия;

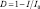– избыточность.

Рассмотрим числовые вероятностные характеристики для следующих геометрических фигур при условии равновероятного распределения:

011 (А) 110 (В)

001 100

111 111

В тех случаях, когда значения xi могут принимать с равной вероятностью только лишь одно из двух равновероятных значений (0 либо 1), т.е. когда значения дискретных случайных величин X не зависят от предыстории, имеем Pi = P = 0,5.

Как видно, фигура (В) представляет собой повернутый на 90 градусов вариант фигуры (А). При этом получим следующие значения начальных моментов первого порядка:

m1А = 1/9*(0*0.5 + 0*0.5 + 1*0.5 +  0*0.5 + 1*0.5 + 1*0.5 +  1*0.5 + 1*0.5 + 1*0.5) = 3/9 = 0.3.

m1В = 1/9*(1*0.5 + 0*0.5 + 0*0.5 +  1*0.5 + 1*0.5 + 0*0.5 +  1*0.5 + 1*0.5 + 1*0.5) = 3/9 = 0.3.

Для центральных моментов первого порядка:

u1A = ((0 – 0.3)*0.5 + (0 – 0.3)*0.5 + (1 – 0.3)*0.5 + + (0 – 0.3)*0.5 + (1 – 0.3)*0.5 + (1 – 0.3)*0.5 +  (1 – 0.3)*0.5 + (1 – 0.3)*0.5 + (1 – 0.3)*0.5) = 1.65.

u1В = ((1 – 0.3)*0.5 + (0 – 0.3)*0.5 + (0 – 0.3)*0.5 +  (1 – 0.3)*0.5 + (1 – 0.3)*0.5 + (0 – 0.3)*0.5 +  (1 – 0.3)*0.5 + (1 – 0.3)*0.5 + (1 – 0.3)*0.5) = 1.65.

Совершенно очевидно, что, вычисляя аналогичным образом, получаем равенство как начальных, так и центральных моментов и энтропии для данных типов изображений:

miA = miB (начальные моменты);

uiA = uiB (центральные моменты);

g1A = g1B (асимметрия);

g2A = g2B (эксцесс);

sA = sB (дисперсия).

Легко проверить, что при условии зависимого распределения вероятностей получаются аналогичные тождества.

Таким образом, показано, что числовые характеристики при условии нормирования изображения изоморфны к масштабированию и повороту.

Рассмотрим характеристики следующих бинарных изображений.

Для каждого из изображений, приведенных на рис. 1, найдем их числовые характеристики, сведя их в табл. 1.

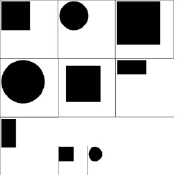
Рис. 1. Бинарные изображения для экспериментальной оценки

Результаты исследования и их обсуждение

Как видно, числовые вероятностные характеристики изображений обладают следующими свойствами:

– числовые характеристики различны для разных геометрических фигур;

– характеристики идентичны и в случае разномасштабных изображений с одинаковой геометрией;

– характеристики идентичны также в том случае, если сравниваемые одинаковые изображения имеют различную ориентацию, вызванную поворотом либо зеркальным отражением;

– характеристики различны в случае сдвига изображений в анализируемом поле;

– среднеквадратичное отклонение может быть одинаково для фигур, имеющих одинаковую площадь;

– коэффициенты асимметрии и эксцесса могут быть равными по модулю, но различными по знаку для отличающихся геометрий.

Очевидно, что любое изображение можно рассматривать как совокупность простейших графических примитивов.

Таким образом, для анализа геометрических особенностей с целью однозначной идентификации сравниваемых изображений необходимо и достаточно одновременное использование коэффициентов среднего значения, среднеквадратичного отклонения, асимметрии и эксцесса, разбивая исходное изображение на составляющие его компоненты.

Как видно из (10), рассматривая изображения как нормально распределенный зависимый случайный процесс, велика вычислительная сложность определения числовых характеристик, так как в общем случае значения вероятностей дискретных случайных величин необходимо определять по формуле Бернулли.

Таблица 1

Рис. 2. Графические примитивы

Таблица 2

Введем понятие квазивероятности P0, такой, что

P(xi) = P0 ∀ i и ,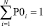

где N – количество пикселей изображения. Тогда исходное изображение можно рассматривать как нормальный равновероятный процесс. В этом случае формулы (10) преобразуются следующим образом (11):

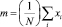– среднее;

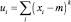– центральные моменты;

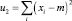– дисперсия;

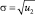– среднеквадратичное отклонение;

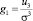– асимметрия;

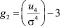– эксцесс.

Рассмотрим граничные условия, при которых можно определить погрешность идентификации изображений. Для этого определим ряд графических примитивов, представляющих собой бинарные нормированные геометрические фигуры с целью их взаимной трансформации и определения той величины искажений, при которых идентификация является возможной.

Как видно из табл. 2, идентификация и в этом случае происходит аналогичным образом.

Введем метрику различия одного изображения от другого. В качестве метрики зададим следующую функцию:

M = (g1a – g1b)2 + (g2a – g2b)2 + + (sa – sb)2 + (ma – mb)2,

где a и b – идентифицируемые изображения.

Как легко можно видеть, использование формулы (11) для изображений табл. 2 дает достаточную оценку близости сравниваемых фигур. При этом минимальная метрика (равная М = 0,89), при которой идентификация еще возможна, получается при использовании фигур 1 и 5. Если теперь подсчитать среднеквадратичное отклонение для яркостей пикселей данных фигур, то получим значение ~10 %.

Заключение

Таким образом, как показано выше, возможна идентификация изображений по предлагаемому методу в том случае, если среднеквадратичное отклонение между изображениями не превышает 10 %. Данный метод распознавания может быть использован в таких областях, как Smart House [4], системы поддержки управленческих решений [5, 6] и др.

Библиографическая ссылка