Локализация загрязненных участков снежного и ледового покрова по изменению отражательной способности может основываться на сравнении значений спектральной индикатрисы рассеяния, определенных для выбранных гладких участков поверхности с заранее подготовленными значениями для снега и льда с заведомо известным уровнем и типом загрязнения. Вычисление индикатрисы рассеяния при известном освещении и рельефе является одной из двух обратных задач по отношению к задаче моделирования изображения рельефа. Другой обратной задачей является задача «shape from shading» восстановления формы рельефа по изображению при известном освещении и индикатрисе рассеяния.
В случае, когда речь идет не о выпуклых участках поверхности, то наблюдаемое изменение цветовых характеристик льда и снега может быть вызвано как наличием изменений в физико-химическом составе (в том числе загрязнений), так и эффектом многократного отражения падающего света в складке поверхности. Под складкой будем понимать область поверхности, в которой может возникать переотражение падающего света и которая может быть наблюдаема посредством видеосъемки с воздуха, в том числе в режиме полета БПЛА.
Рис. 1. Примеры торосов на арктической поверхности
Расположение таких складок на снежно-ледовой поверхности характерно для участков с торосистой поверхностью, которые являются распространенным явлением в Арктике. Торосы представляют собой нагромождение обломков льда, которые образуются в результате сжатия ледяного покрова и могут достигать до 10–20 метров в высоту. Пример торосов приведен на рис. 1. Таким образом, участки поверхности, потенциально имеющие эффект переотражения, могут достигать заметных размеров и их исследование необходимо в задаче определения загрязненных участков по изменению отражательной способности.
Важно отметить, что загрязнения арктической поверхности (в частности, вызванные разливами нефти) приводят к изменениям отражательных характеристик свойств снега и льда, которые в свою очередь могут становиться причиной различных климатических аномалий и изменений, включая таяние и разрушение льдов [1].
Работа состоит из четырех частей. В первой части рассматривается постановка задачи цветовой константности. Во второй части приводится описание линейных и мультипликативно-замкнутых спектральных моделей. В третьей части обсуждается эффект многократного отражения применительно к наблюдению складок на поверхности Арктики. В четвертой части приведено заключение.
Постановка задачи цветовой константности
Сложность задачи цветовой константности (ЦК) или цветопостоянства заключается в восстановлении окраски наблюдаемой поверхности по зарегистрированным сенсором спектральным характеристикам излучения при неизвестной цветности освещения сцены. Даже если наблюдение ведется при освещении сцены одним источником, могут возникать переотражения, при которых спектр освещения изменяется – умножается на спектр окраски поверхности. Вследствие этого мы имеем дело с тем, что разные точки поверхности оказываются освещены излучением разного спектрального состава.
Применительно к задачам компьютерного зрения изучение вопроса цветовой константности [3, 4] является актуальным при создании алгоритмов детекции объектов, распознавания образов, стереоотождествления и др.
В общем случае математическая постановка задачи цветовой константности является некорректной, так как подразумевает восстановление бесконечномерных спектров освещения и окраски по маломерной реакции сенсора. Для того, чтобы снять данную неопределенность, при рассмотрении вводят модельные предположения о спектральных свойствах окраски, свойствах освещения и наблюдаемых поверхностей. Модельные предположения позволяют выделить на изображении эффекты, которые принято называть ключами константности и наличие которых позволяет решить задачу ЦК.
Приведем несколько подходов к выбору ключа константности применительно к нашей задаче. В классическом подходе предполагается, что на наблюдаемой поверхности всегда содержится белый объект, для которого цветность отраженного излучения соответствует цветности источника освещения [5]. В алгоритме «gray world» [6] ключом является всё изображение, так как предполагается, что средние интенсивности по каждому RGB-каналу равны между собой. Необходимо отметить, что в случае большого размера загрязнения, наблюдаемого БПЛА, оба сформулированных предположения могут быть не выполнены.
Предложение использовать в качестве ключа константности складку поверхности сделано в работе [7]. При освещении складки поверхности возникает множественное отражение падающего света, что приводит к изменению спектральных характеристик цвета в различных точках складки. При этом показано, что спектр отраженного света в различных точках складки подчиняется некоторым закономерностям.
Спектральные модели
Рассмотрим модель цветного изображения трехмерного объекта:
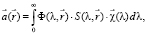(1)
где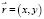 
– координаты точки на изображении, λ – длина волны, 
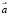– регистрируемое изображение, Φ – спектр окраски, S(λ) – спектр освещения, 
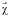– вектор чувствительности сенсора. Как правило, используются трехканальные сенсоры, то есть вектор 
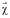имеет 3 компоненты. Для решения задачи оценки окраски поверхности (решения задачи ЦК) необходимо при известном 
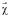оценить Φ по 
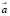. Фактически речь идет о восстановлении функции в каждой точке по трем числам.
Предположим, что в наблюдаемой сцене присутствует трехмерный объект, спектр окраски которого одинаков для всей поверхности. В этом случае при освещении поверхности преимущественно одним диффузным источником света уравнение (1) может быть записано в следующем виде:
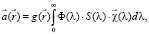(2)
где g – неизвестная функция, зависящая от геометрии сцены [2].
Определение спектра окраски Φ(λ) согласно (2) является некорректной задачей, так как Φ(λ) – функция, которая определена для всех неотрицательных вещественных чисел, а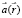 
является трехмерным вектором. Предположение, что Φ(λ) может описываться моделью, позволяет решить проблему корректности задачи ЦК.
К часто используемым спектральным моделям можно отнести линейные спектральные модели (спектрозональная модель, модель Ильмаза), в которых пространство спектральных функций ограничивается некоторым трехмерным линейным подпространством. Их существенным недостатком является проблема цветопередачи, которая заключается в невозможности адекватной аппроксимации спектров излучений и окрасок высокой насыщенности. Это объясняется тем, что узкополосные спектры, различающиеся сдвигом по оси длин волн (чьи цвета различаются тоном), линейно независимы.
Избежать проблемы цветопередачи позволяет использование гауссовской спектральной модели (ГСМ), обладающей преимуществом мультипликативной замкнутости. В ГСМ верно утверждение, что результат перемножения двух функций, входящих в семейство модели, также входит в семейство. Использование ГСМ позволяет упростить построение алгоритмов ЦК за счет аналитической интегрируемости интеграла реакций (1).
В общем виде ГСМ выглядят следующим образом:
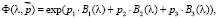(3)
где Bi (λ) – базисные функции,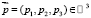 
– вектор параметров модели.
Для ГСМ вектор базисных функций выглядит следующим образом:
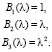(4)
Для определения окраски в точке с показанием сенсора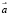 
необходимо решить задачу оптимизации в пространстве параметров спектральной модели:
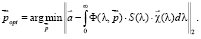(5)
Спектр окраски с параметрами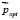 
доставляет минимум между оценкой отклика и зарегистрированным сенсором откликом.
При этом каждая точка складки получается освещенной не только первичным источником света, но и переотраженным светом от стенок складки [8]:
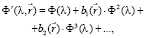(6)
где bi – некоторые коэффициенты, характеризующие геометрию сцены.
В ГСМ допустимо следующее приближение:
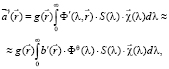(7)
где θ > 1,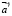 
– отклик сенсора на луч в случае многократного отражения.
Таким образом, зафиксировав на границе складки два различных отклика сенсора на одну и ту же окраску внутри и вне складки, можно получить вдвое больше данных для решения задачи восстановления спектральной функции окраски.
Использование эффекта многократного отражения на снежно-ледовой поверхности для решения проблемы метамерии окрасок
Метамерией называется явление, когда два излучения с разными спектральными составами формируют одинаковый отклик сенсора. В задачах экологического мониторинга возможна ситуация, когда спектральный состав чистой снежно-ледовой поверхности оказывается метамерен спектральному составу загрязнения, то есть ответы сенсора оказываются неразличимыми. Рассмотрение складок поверхности в качестве ключа ЦК дает способ решения этой проблемы.
В качестве сенсора при наблюдении снежно-ледовой поверхности в Арктике в режиме полета БПЛА выступает оптическая система, в общем случае удовлетворяющая следующим двум условиям. Первое из них заключается в получении изображений наблюдаемой поверхности, являющихся предметом непосредственного изучения. Второе условие – получение изображений небосвода, для чего можно использовать дополнительное устройство видеозахвата, установленное на БПЛА и включающее широкоугольный объектив для охвата полусферы неба. Получаемое изображение небосвода может использоваться для получения оценки спектрального состава излучения [9].
При известных параметрах сенсора и оценке спектрального состава излучения возможно восстановление спектра окраски в гауссовской спектральной модели с целью последующего их сравнения с эталонными параметрами чистого снежно-ледового покрова и известных загрязнений. Однако вследствие эффекта метамерии окрасок совпадение параметров еще не гарантирует совпадение спектральных составов.
Фиксация излучения после многократного отражения в различных точках складки с применением ГСМ (рис. 2) позволяет получить независимую оценку параметров окраски. Под независимостью здесь понимается, что в ситуации, когда прямые отражения света от поверхностей двух разных окрасок оказались метамерными, многократные переотражения от поверхностей складок двух тех же окрасок гарантированно метамерными не окажутся.
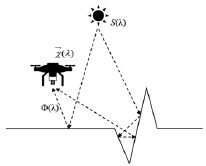
Рис. 2. Схема наблюдения эффектов отражения и многократного отражения в складке
Стоит отметить, что несмотря на то, что исследователями уже получены частные экспериментальные подтверждения применимости ГСМ и использования в качестве ключа константности складку для изучения эффекта переотражения на различных поверхностях [10], дальнейшее развитие этого подхода для анализа изображений рельефа снежно-ледовой поверхности требует глубокой практической проработки как на уровне обработки синтетических данных, так и фото/видеоданных, полученных в ходе натурных наблюдений.
Заключение
В работе с использованием спектральной модели ГСМ описаны эффекты многократного отражения при анализе цветных изображений. Для моделирования эффекта переотражений предложено решение задачи цветовой константности, базирующееся на использовании в качестве ключа константности однородно окрашенной складки поверхности. При известных спектральных характеристиках сенсора показана применимость данного ключа для обработки цветных изображений при освещении поверхности одним диффузным источником, в случае когда одна из базисных функций спектральной модели является константой.
Предложенный подход позволяет при анализе цветных изображений Арктики интерпретировать данные об изменении отражательной способности снега и льда на участках с торосистой поверхностью, для которых наличие эффекта многократного отражения объясняется особенностями рельефа. В частности, на изображении, получаемом при наблюдении с БПЛА, могут быть детектированы «видимые» области складок торосов. При отклонениях в складке значений спектра окраски поверхности от значений спектра окраски «чистого» снега и льда может быть сделано предположение о наличии загрязнения.
Работа проводилась при поддержке грантов РФФИ № 15-29-06091 (офи_м) и 15-29-06080 (офи_м).
Библиографическая ссылка
Путинцев Д.Н., Арлазаров Н.В., Усилин С.А., Кац В.А. ИСПОЛЬЗОВАНИЕ ЭФФЕКТОВ МНОГОКРАТНОГО ОТРАЖЕНИЯ ПРИ АНАЛИЗЕ ЦВЕТНЫХ ИЗОБРАЖЕНИЙ СНЕЖНО-ЛЕДОВОЙ ПОВЕРХНОСТИ АРКТИКИ В ЗАДАЧАХ ЭКОЛОГИЧЕСКОГО МОНИТОРИНГА // Современные наукоемкие технологии. – 2017. – № 5. – С. 58-62;URL: https://top-technologies.ru/ru/article/view?id=36668 (дата обращения: 21.11.2024).