Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Питухин А.В. 1 Шиловский В.Н. 1 Костюкевич В.М. 1

---

1 ФГБОУ ВПО «Петрозаводский государственный университет»

Для эффективной организации ремонтных работ необходимо знание характеристик интенсивности заявок на определенный вид ремонта, на замену деталей машин на соответствующих специализированных участках предприятия технического сервиса и ремонта. В статье представлена методика и апробация методики оценки соответствия потока отказов деталей лесозаготовительных машин простейшему с помощью статистического моделирования. Применение результатов моделирования потоков может быть использовано при расчете потребности запасных частей, определении и распределении ремонтных работ по объектам ремонтно-обслуживающей базы. Исследована зависимость сходимости суммарного потока отказов деталей лесных машин к простейшему от величины среднего ресурса деталей, коэффициента вариации, числа суммируемых потоков. Приведены результаты статистического моделирования сходимости суммарного потока замен деталей к простейшему при Вейбулловском и нормальном распределении ресурсов деталей.

Статья в формате PDF

0 KB

отказ

поток отказов

закон распределения

моделирование

1. Быков В.В. Моделирование системы технического сервиса: монография / В.В. Быков, А.С. Назаренко, Н.К. Юрков. – М.: Изд-во МГУЛ, 2004. – 84 с.

2. Вайнштейн И.И. Оптимизация порядка замен по минимуму среднего числа отказов при эксплуатации технических систем / И.И. Вайнштейн, Г.Е. Михальченко, В.И. Вайнштейн // Проблемы машиностроения и надежности машин. – М.: Изд-во «Наука», 2012. – № 5. – С. 85–90.

3. Кельберт М.Я. Вероятность и статистика в примерах и задачах. Том 1. Основные понятия теории вероятностей и математической статистики / М.Я. Кельберт, Ю.М. Сухов. – М.: МЦНМО, 2010. – 488 c.

4. Лукин В.Л. Статистический контроль динамики интенсивности отказов технических систем в течение жизненного цикла / Лукин В.Л., Сухорученков Б.И., Белоглазов В.А., Швед Е.В. // Двойные технологии. – 2012. – № 3. – С. 18–25.

5. Михайлов Г.А. Численное статистическое моделирование. Методы Монте-Карло / Г.А. Михайлов, А.В. Войтишек. – М.: Академия, 2006. – 368 с.

6. Питухин А.В. Надежность лесозаготовительных машин и оборудования: Учеб. пособие / А.В. Питухин, В.Н. Шиловский, В.М. Костюкевич. – СПб.: Изд-во Лань, 2010. – 288 с.

7. Шиловский В.Н. Теоретические основы и стратегии организации маркетинга и менеджмента технического сервиса территориально распределенных машин и оборудования: монография. – Петрозаводск: ПетрГУ, 2001. – 324 с.

8. Gerasimov Yu.Yu. Development Trends and Future Prospects of Cut-to-length Machinery / Yu.Yu. Gerasimov, A.P. Sokolov, V.S. Syunev // Advanced Materials Research. – 2013. – Vol. 705. – P. 468–473.

Общие положения

Метод статистического моделирования позволяет решать весьма сложные задачи и применим тогда, когда аналитические методы не могут быть использованы. Он позволяет полнее учесть особенности системы, использовать любые законы распределения случайных величин, имеет наглядную вероятностную трактовку, простую вычислительную схему [1–3].

Суть метода состоит в следующем:

а) получение с помощью датчика случайных чисел совокупности реализаций случайной величины (случайной выборки заданного объема) с заданным законом распределения;

б) имитационное моделирование рассматриваемого процесса;

в) формулирование выводов о характеристиках процесса по результатам проведенного моделирования.

Многократное повторение указанных действий позволяет получить достаточную выборку для оценки закона распределения и других статистических характеристик.

Целью проведенного моделирования явилось подтверждение сходимости потока отказов лесных машин к простейшему. Перед процессом моделирования проведены экспериментальные исследования законов распределения ресурса деталей и сборочных единиц тракторов ООО «ОТЗ» и машин на их базе, позволившие выявить следующие основные законы распределения ресурса лесных: нормальное распределение и распределение Вейбулла [7, 8].

При моделировании исследовался закон распределения интервалов времени (наработки) между отказами суперпозиции Np потоков. Суммарный поток при увеличении Np приближается к простейшему.

Требуется при заданном промежутке контроля процесса (0; Тконтр) оценить параметр интенсивности отказов λ соответствующего показательного распределения:

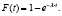
По результатам оценки параметра проверяется гипотеза о соответствии суммарного потока показательному закону [7, 6].

Материалы и методы исследования

Моделируется совокупность Np потоков событий, каждый из которых характеризуется одним и тем же видом закона распределения длины промежутка между соседними событиями. Начальный момент для каждого потока событий случаен и равномерно распределен на промежутке (0, τ), где τ соответствует периоду ввода соответствующей машины в эксплуатацию. Каждый поток событий имеет следующие характеристики [4]:

- начальное математическое ожидание соответствующего закона распределения – М1;

- коэффициент уменьшения математического ожидания после первого отказа – k.

После реализации первого события вид закона распределения потока и коэффициент вариации сохраняются, математическое ожидание становится равным

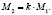
В момент времени, превосходящий продолжительность функционирования соответствующей машины до списания (tсп), происходит «Замена машины», то есть математическое ожидание становится равным начальному значению М1 и процесс моделирования повторяется.

Алгоритм моделирования состоит в генерации значений начальных моментов τi для каждого – i-го потока 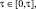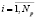. Затем определяются моменты реализации первых отказов 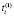, рассчитывается первый интервал суммарного потока (Ti):

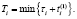
После этого генерируется момент следующего отказа для j-го потока:

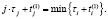
Второй интервал суммарного потока вычисляется как

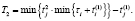
Аналогично рассчитываются последующие интервалы. При этом проверяются условия замены:

а)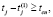

где tj – момент текущего события j-го потока;

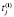– события j-го потока при предыдущей замене и условия окончания процесса;

tсп – продолжительность работы машины до списания.

б) T ≥ Тконтр,

где T – момент текущего события суммарного потока.

По окончании процесса для контроля определяются:

mi – среднее наблюдаемое значение реализации каждого i-го потока;

Vi – соответствующий наблюдаемый коэффициент вариации.

Затем по выборке 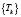рассчитывается показатель λ и по критерию Колмогорова определяется вероятность совместимости с выборкой гипотезы о распределении 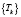по показательному закону [3, 5].

При моделировании процесса потока отказов лесных машин требуется выбрать начальные условия. В качестве исходных данных для решения поставленной задачи должны быть заданы:

- Tконт – продолжительность контроля процесса;

- k – коэффициент уменьшения математического ожидания после первого отказа;

- tсп – продолжительность работы машины до списания;

- f(x) – закон распределения (предусмотрено использование двух законов распределения – Вейбулла и нормального);

- τ – интервал ввода машины в действие;

- Np – количество машин (потоков);

- V – коэффициент вариации составляющих потоков;

- M – математическое ожидание (начальное значение) составляющих потоков (отказов).

До исходных данных после основного блока вводятся данные со значениями таблиц для расчета значения вероятности по критерию Колмогорова λ (эти данные прилагаются к основному блоку данных) [3, 5].

Количество машин (потоков), принимаемых для моделирования, выбирается исходя из величины парка этих машин, эксплуатируемых на одном предприятии или цехе. Для моделирования выбираются условные парки машин в количестве от 1 до 12 единиц.

Средний ресурс наиболее часто отказывающих деталей машин изменяется от 500 до 4000 моточасов. Значения средних ресурсов деталей, превышающих средний ресурс до списания машин, не могут быть использованы для моделирования, так как физическая сущность процесса в этом случае становится неопределенной. Исходя из этих положений для исследования выбираем значения средних ресурсов деталей до замены от 500 до 4000 с шагом 500 моточасов.

Значения коэффициентов вариации для соответствующих распределений будут следующими:

а) для нормального: 0,2–0,4 с шагом 0,1;

б) для распределения Вейбулла: 0,4–0,7 с шагом 0,1.

Моменты отказов (и их потоков) являются случайными величинами, функции распределения которых зависят от одного (для однопараметрического распределения) или нескольких (для нормального распределения, закона Вейбулла) параметров. Следовательно, суммарные потоки являются функциями от значений этих параметров и в результате моделирования отличаются от реализации к реализации. С увеличением числа реализаций сходимость улучшается. Проблема статистической сходимости заключается в выборе числа реализаций, обеспечивающих заданную точность результатов моделирования. Общее число реализаций должно быть таким, чтобы точность случайной величины была не ниже заданной.

Для проверки результатов моделирования оценивается параметр λ соответствующего показательного закона распределения и проверяется гипотеза о соответствии ему суммарного потока. Проверка согласия определяется по критерию Колмогорова. Для правильного применения критерия Колмогорова необходимо соблюдение следующих требований: недопустимо объединение статистических данных в разряды, так как критерий Колмогорова основан на индивидуальных значениях непрерывной случайной величины; должны быть известны функция распределения и ее параметры.

Результаты исследования и их обсуждение

В таблицах приведены результаты моделирования сходимости суммарного потока замен деталей, сборочных единиц к простейшему при Вейбулловском (v = 0,5) и нормальном (v = 0,3) распределениях ресурса деталей лесных машин.

Результаты моделирования потока отказов деталей и сборочных единиц лесных машин показали, что сходимость суммарного потока к простейшему потоку при Вейбулловском и нормальном законах распределения зависит от величины среднего ресурса детали или сборочной единицы, коэффициента вариации, числа суммируемых потоков.

Выводы

1. Результаты моделирования потока отказов деталей лесных машин показали, что сходимость суммарного потока к простейшему наблюдается в отдельных случаях при суммировании 3–4 потоков, но в большинстве случаев при суммировании 5–7 потоков.

2. Полученные результаты моделирования могут быть использованы в виде таблиц для определения минимального числа потоков, при котором можно считать суммарный поток простейшим.

3. Применение результатов моделирования потоков замен возможно при расчете потребности запасных частей, определении и распределении ремонтных работ по объектам ремонтно-обслуживающей базы, по предприятиям и цехам пунктов и станций технического сервиса, в том числе по предприятиям массового обслуживания открытого типа.

Библиографическая ссылка