В работах [3, 8] предложена модель гармонической псевдоэмоции робота [5], введено понятие амплитуды псевдоэмоции и доказано, что гармоническая псевдоэмоция является псевдоэмоцией. В работе [9] была описана модель амбивалентных псевдоэмоций робота. Настоящая статья посвящена описанию модели амбивалентных гармонических псевдоэмоций робота – амбивалентные псевдоэмоции робота будут представлены в гармоническом виде, даны основные определения и описаны основные свойства амбивалентных гармонических псевдоэмоций.
Математическая модель гармонической псевдоэмоции
В монографии [6] дано следующее определение псевдоэмоции эмоционального робота.
Определение 1. Функция [1] внутренних переживаний робота M(t) называется псевдоэмоцией робота, если она удовлетворяет условиям:
1. Область определения M(t):t0[t0, T0], 0 < t0 < T0 < ∞.
2. M(t) – дифференцируемая на (t0, T0), непрерывная и однозначная функция на [t0, T0].
3. M(t0) = 0 и M(T0) = 0.
4. В области определения существует единственная точка z, такая, что z ≠ 0, z ≠ T0 и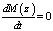 
[6].
Также, в монографии [6] было дано следующее определение эмоционального такта.
Определение 2. Тактом называется время действия одной псевдоэмоции.
В работе [3] дано определение гармонической псевдоэмоции робота.
Определение 3. Гармонической псевдоэмоцией назовем функцию вида
,
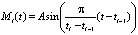где A – вещественная константа; t – время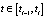 
– время начала такта с порядковым номером i; ti – время окончания такта с порядковым номером i.
A называется амплитудой гармонической псевдоэмоции робота.
В работе [9] дано следующее определение амбивалентных псевдоэмоций робота.
Определение 4. Амбивалентными называются псевдоэмоции, противоположные друг другу, переживаемые одновременно.
В монографии [6] были определены такие величины, как элементарное воспитание и воспитание робота.
Пара амбивалентных псевдоэмоций (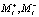
) порождают пару элементарных воспитаний (
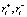), вычисляемых по формуле
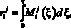
где τ – длительность такта под номером i.
В работе [4] было показано, что справедливо равенство
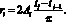
Обозначим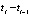 
как Ti – длительность i-ого воспитательного такта.
Воспитательный процесс [2] идет одновременно по паре амбивалентных псевдоэмоций (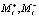
) (поскольку одно и то же внешнее воздействие порождает обе псевдоэмоции), как следствие, 
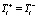для всех i.
Таким образом, справедливы следующие соотношения
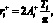
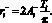
Данные соотношения показывают, что обе из амбивалентных псевдоэмоций робота зависят только от амплитуды псевдоэмоции и длительности воспитательного такта.
Воспитание робота в конце i-ого воспитательного такта рассчитывается по формуле
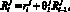(1)
где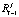 
– воспитание робота в конце (i – 1)-ого воспитательного такта, 
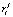– элементарное воспитание, полученное за i-ый такт, 
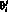– коэффициент памяти робота.
Таким образом, справедливо соотношение
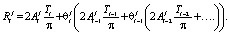(2)
Опишем основные теоремы о гармонических псевдоэмоциях.
Теорема 1. Воспитание эмоционального робота, испытывающего гармонические псевдоэмоции, зависит только от амплитуд этих псевдоэмоций, продолжительности воспитательных тактов и коэффициентов памяти.
Доказательство. Доказательство очевидно следует из вида соотношения (2), однако можно привести и более строгое доказательство.
Докажем, что для шага с номером i теорема справедлива.
Очевидно, что
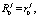
поскольку до начала воспитательных тактов робот не имел воспитания.
Таким образом, справедливо равенство
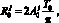(3)
т.е. для i = 0 теорема верна.
Далее, предположим, что теорема верна для такта i – 1 и докажем ее для такта i. Согласно (1), справедливы соотношения
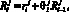
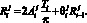
Из последнего соотношения видно, что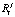 
зависит от амплитуды, длительности такта, коэффициента памяти и предыдущего значения воспитания. Однако, по предположению, предыдущее значение воспитания также зависит от амплитуды, продолжительности такта и коэффициента памяти. Таким образом, 
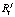зависит от амплитуды, длительности такта и коэффициента памяти, что и требовалось доказать.
Теорема 2. Воспитание эмоционального робота с постоянными коэффициентами памяти, испытывающего гармонические псевдоэмоции с течение одинаковых по времени воспитательных тактов, зависит только от амплитуд испытываемых гармонических псевдоэмоций.
Доказательство очевидно следует из теоремы 1.
Хотя данная теорема и кажется очевидной и не выгладит нужной, она несет в себе практический смысл, поскольку может быть применена для разработки робота с постоянными коэффициентами памяти и длинами воспитательного такта.
Математическая модель амбивалентных гармонических псевдоэмоций
Пусть робот испытывает пару амбивалентных псевдоэмоций (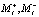
), являющихся гармоническими. Как было показано выше, эти эмоции порождают элементарные воспитания (
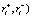, которые, в свою очередь порождают воспитания (
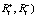. В работе [9] было показано, что общее воспитание робота в конце воспитательного такта i, Ri может быть вычислено по формуле
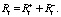
Таким образом, справедлива следующая теорема.
Теорема 3. Суммарное воспитание, порожденное парой амбивалентных гармонических псевдоэмоций, зависит от амплитуд этих гармонических псевдоэмоций, коэффициентов памяти робота и длительности воспитательных тактов.
Доказательство.
По теореме 1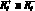 
зависят от амплитуд гармонических псевдоэмоций, коэффициентов памяти робота и длительности воспитательных тактов.
Поскольку справедливо равенство
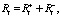
то и Ri зависит от вышеуказанных параметров, ч.т.д.
3. Вычисление значений амплитуд гармонических амбивалентных псевдоэмоций
Пусть эмоциональный робот испытывает гармонические амбивалентные псевдоэмоции. В случае если известны величины воспитаний робота в конце нескольких последовательных фиктивных воспитательных тактов [6], а также коэффициенты памяти робота и длительность воспитательных тактов, согласно теореме 2 можно вычислить амплитуды псевдоэмоций, испытываемых роботом.
Поставим следующую задачу – произведено несколько (не менее 4) замеров эмоционального состояния робота. Известно, что робот испытывал амбивалентные гармонические псевдоэмоции с известной величиной воспитательного такта. Необходимо определить амплитуды псевдоэмоций, испытываемых роботом.
В работе [10] был описан метод определения величин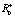 
, 
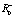, θ+, θ– для эмоционального робота по замерам эмоционального состояния. Пусть нам известна длина воспитательного такта. Она постоянна и равна T. Далее, зная параметры 
, 
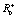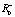, θ+, θ–, мы можем определить 
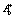и 
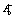по следующим формулам, следующим из соотношения (3).
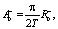
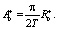
Таким образом, мы можем вычислить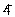 
и 
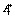по следующим формулам:
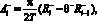(4)
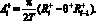(5)
Описанный метод вычисления амплитуд гармонических амбивалентных псевдоэмоций в будущем станет основой для вычисления эмоциональных характеристик робота, а также может быть полезен для создания робота с заданными характеристиками.
Пусть робот на момент начала воспитательного процесса имел воспитание R0, состоящее из пары амбивалентных воспитаний (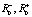
). Далее робот испытывает одну амбивалентную гармоническую псевдоэмоцию (
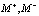) длительностью T, и его воспитание становится равным (
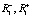). Далее проходит несколько n фиктивных воспитательных тактов, после которых воспитание робота становится равным (
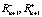). Необходимо вычислить амплитуду псевдоэмоции, испытанной роботом.
Поскольку прошло n фиктивных воспитательных тактов и известны воспитания робота до и после тактов, можно вычислить коэффициенты памяти робота по амбивалентным псевдоэмоциям:
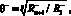
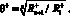
Далее, зная значения θ– и θ+, можно вычислить амплитуды псевдоэмоции А+ и А– по формулам (4) и (5).
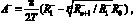(6)
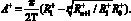(7)
Формулы (6) и (7) показывают, что для определения амплитуды гармонической псевдоэмоции достаточно знать значения воспитаний робота в три момента времени – до псевдоэмоции, после псевдоэмоции и через несколько фиктивных тактов. Данный вывод позволит в дальнейшем описать механизм определения амплитуд гармонических псевдоэмоций.
Анализируя формулу (5), с учетом того, что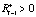 
, можно заметить, что при росте значения θ+ значение функции уменьшается, т.е. амплитуда псевдоэмоции уменьшается по модулю.
Анализируя формулу (4), с учетом того, что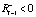 
, можно заметить, что при росте значения θ– растет и значение функции (4). Однако, учитывая, что данная функция всегда отрицательна (поскольку описывает отрицательную псевдоэмоцию), можно сказать, что ее модуль уменьшается, т.е. амплитуда уменьшается по модулю.
Таким образом, можно сказать, что при увеличении коэффициентов памяти амплитуда псевдоэмоции уменьшается по модулю, т.е. робот переживает менее сильный эмоциональный пик.
Заключение
В статье впервые предложена модель амбивалентных гармонических псевдоэмоций робота, описаны алгоритмы расчета амплитуд гармонических амбивалентных псевдоэмоций робота, показана зависимость амплитуд псевдоэмоций от коэффициентов памяти робота, а также предложен алгоритм расчета амплитуды псевдоэмоции робота по трем воспитаниям робота.
Библиографическая ссылка
Шафер А.Е. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ГАРМОНИЧЕСКИХ АМБИВАЛЕНТНЫХ ПСЕВДОЭМОЦИЙ РОБОТА // Современные наукоемкие технологии. – 2017. – № 4. – С. 56-59;URL: https://top-technologies.ru/ru/article/view?id=36639 (дата обращения: 21.11.2024).