Существующие методы и алгоритмы обработки сигналов и телевизионных изображений позволяют решить задачу достоверной обработки с условием, что задана априорная информация об обрабатываемом процессе, что является не всегда возможным [1]. Для получения такой информации, как правило, требуются дополнительные технические решения, которые являются достаточно сложными и не всегда технически реализуемыми.
Одним из источников получения информации при анализе телевизионного изображения являются его производные. Определение производных является одним из актуальных вопросов в задаче обработки телевизионных изображений при наличии шума. Существующие методы предварительной обработки измерительных данных связаны в основном с использованием цифровых фильтров. В тех случаях, когда в процессе обработки подавляется высокочастотная составляющая, говорят о сглаживании [9–12].
Методы, основанные на сплайнах, заняли прочное место среди наиболее мощных средств вычислительной математики. В практике обработки сигналов и изображений широко используется сплайн-аппроксимация их дискретных значений, что определяется свойством гладкости аппроксимирующей функции по производным на границах интервалов дискретизации [3–8].
В настоящее время выделение контуров телевизионных изображений производят, как правило, с использованием различных масок, то есть по сути дела используют методы численного дифференцирования. Однако при наличии интенсивных фоновых шумов такой подход, как правило, непродуктивен и приводит к большим погрешностям.
Таким образом, задача разработки методов и алгоритмов дифференцирования изображений для выделения контуров объектов на телевизионных изображениях при наличии интенсивного фонового шума в настоящее время является актуальной.
Цель настоящей работы: разработка нового метода выделения контуров телевизионных изображений с использованием сплайн-дифференцирования.
Анализ алгоритма сплайн-дифференцирования сигналов
В настоящее время существует ряд задач обработки сигналов, когда регистрируется процесс S(t), а информативным параметром для дальнейшей обработки является его первая производная 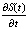 . Известные к настоящему времени методы численного дифференцирования позволяют решать такую задачу лишь для функций, заданных в известных точках с малой погрешностью.
. Известные к настоящему времени методы численного дифференцирования позволяют решать такую задачу лишь для функций, заданных в известных точках с малой погрешностью.
Рассмотрим одно из широко используемых в практике разностных отношений, для приближенного вычисления производной функции S(t), например [9]:
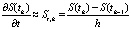 , (1)
, (1)
где h – шаг, S(tk) – выборочные значения сигнала.
Методическая погрешность аппроксимации в данном случае определится следующим выражением:
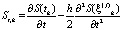 , (2)
, (2)
где 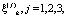 – точки из интервала
– точки из интервала 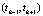 .
.
Погрешность, которая возникает при вычислении данных разностных отношений, может намного превосходить погрешность в задании значений функции S(tk) и в некоторых случаях неограниченно возрастать при стремлении шага сетки h к нулю.
Выражение (2) в данном случае является некорректным. Это связано с тем, что для нахождения приближения St,k к 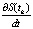 необходимо, чтобы шаг h был малым. Задачу дифференцирования также можно решить с использованием полиномов Лагранжа, но для высокоточной аппроксимации придется использовать большие степени этих полиномов, что неизбежно приводит к осцилляциям. Практического применения данный подход не нашел.
необходимо, чтобы шаг h был малым. Задачу дифференцирования также можно решить с использованием полиномов Лагранжа, но для высокоточной аппроксимации придется использовать большие степени этих полиномов, что неизбежно приводит к осцилляциям. Практического применения данный подход не нашел.
В настоящее время математический аппарат сглаживающих В-сплайнов применяется для решения широкого круга задач. Применение на практике данного метода аппроксимации сплайнами дифференцированных сигналов позволяет значительно уменьшить время обработки по сравнению с другими численными методами.
Рассмотрим предлагаемый метод на примере численного сплайн-дифференцирования известного сигнала [2]. Будем проводить математическое моделирование с использованием пакета математического моделирования Маткад 14.
Например, пусть тестовый сигнал имеет следующий вид:
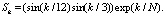 (3)
(3)
Примем следующие обозначения Sk = S(tk), где N = 512 – количество отсчетов, 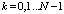 . Для такого представления легко найти аналитическую производную
. Для такого представления легко найти аналитическую производную 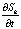 .
.
Вычислим аналитическую производную Sk:
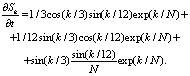 (4)
(4)
В данном случае разностное соотношение численного дифференцирования будет иметь следующий вид:
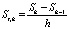 , (5)
, (5)
где h – шаг сетки.
Проведенный авторами вычислительный эксперимент показал, что значения производной St,k практически совпадают со значениями 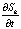 , вычисленными аналитически.
, вычисленными аналитически.
Вычислим коэффициенты сплайн-функции, аппроксимирующей тестовый сигнал в соответствии методом [2]. При этом значения производной 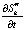 , полученные методом сплайн-дифференцирования, практически совпадают со значениями производной сигнала
, полученные методом сплайн-дифференцирования, практически совпадают со значениями производной сигнала 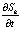 , вычисленной аналитически, это свидетельствует о корректности предложенного подхода.
, вычисленной аналитически, это свидетельствует о корректности предложенного подхода.
Для учета погрешности регистрации добавим с использованием датчика случайных чисел к исходному сигналу Sk «белый» гауссовский шум N1, со следующими параметрами mN = 0, Dш:
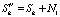 . (6)
. (6)
Проведем численное дифференцирование полученной аддитивной смеси сигнала и шума 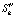 с помощью разностной схемы.
с помощью разностной схемы.
Из рис. 1 следует, что значения St,k, полученные с использованием метода разностного дифференцирования, существенно отличаются от значений аналитической производной 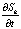 данного сигнала. Это означает, что на практике данный метод использовать невозможно. Для удобства рассмотрения на рис. 1 представлены первые 64 отсчета.
данного сигнала. Это означает, что на практике данный метод использовать невозможно. Для удобства рассмотрения на рис. 1 представлены первые 64 отсчета.
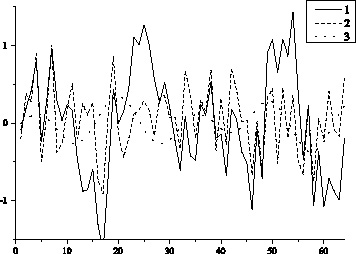
Рис. 1. 1 – 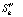 ; 2 –
; 2 – 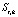 ; 3 –
; 3 – 
Рассмотрим дифференцирование аддитивной смеси сигнала и шума 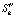 с помощью предложенного метода сплайн-дифференцирования. На рис. 2 приведены результаты вычислительного эксперимента с использованием предложенного метода и разностной схемы. Как следует из рисунка, производная аддитивной смеси сигнала и шума успешно восстановлена при помощи предложенного метода сплайн-дифференцирования.
с помощью предложенного метода сплайн-дифференцирования. На рис. 2 приведены результаты вычислительного эксперимента с использованием предложенного метода и разностной схемы. Как следует из рисунка, производная аддитивной смеси сигнала и шума успешно восстановлена при помощи предложенного метода сплайн-дифференцирования.
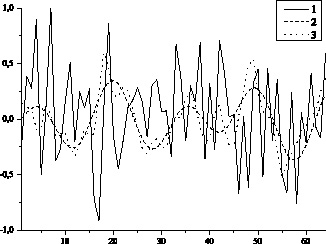
Рис. 2. 1 – 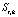 , 2 –
, 2 – 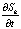 ; 3 –
; 3 – 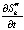
Для оценки точности дифференцирования дисперсия ошибки восстановления рассчитывалась в соответствии со следующими выражениями:
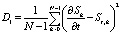 , (7)
, (7)
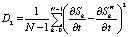 , (8)
, (8)
где D1 – дисперсия ошибки для разностной схемы вычисления производной, D2 – дисперсия ошибки для производной сигнала, дифференцированного с использованием сплайнов.
Таким образом, предложенный метод дает возможность дифференцировать результаты измерений с существенно меньшей погрешностью, чем разностная схема. При этом погрешность дифференцирования практически не меняется при увеличении дисперсии шума (погрешности регистрации).
Рассмотрим использование предложенного метода на примере дифференцирования строки изображения.
Анализ алгоритма сплайн-дифференцирования изображений
На рис. 3 приведен результат нахождения производной 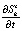 строки изображения
строки изображения 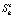 на фоне шума с использованием предложенного метода. Размер выборки был равен N = 512. Очевидно, что метод сплайн-дифференцирования достаточно устойчив к шуму по сравнению с разностной схемой.
на фоне шума с использованием предложенного метода. Размер выборки был равен N = 512. Очевидно, что метод сплайн-дифференцирования достаточно устойчив к шуму по сравнению с разностной схемой.
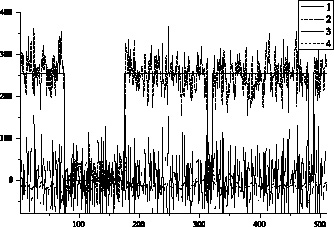
Рис. 3. 1 – 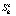 , 2 –
, 2 – 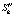 , 3 –
, 3 – 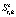 , 4 –
, 4 – 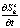
Таким образом, применение предложенного метода дифференцирования строки изображения на фоне шума позволяет с достаточной точностью вычислить производную. Имея информацию о поведении первой производной, можно определять локальные максимумы в строке изображения на фоне шума.
Процедура нахождения первой производной сигнала с использованием метода сплайн-дифференцирования следующая:
1. Выбирается коэффициент сглаживания (как правило, равен единице, при высоком уровне шума можно выбрать больший коэффициент).
2. Вычисляется матрица коэффициентов сглаживания.
3. Решается система линейных алгебраических уравнений с учетом коэффициентов сглаживания и значений входной реализации, тем самым вычисляются коэффициенты сглаживающих сплайнов.
4. С помощью сглаживающих В-сплайнов восстанавливается первая производная и исходный сигнал.
Метод выделения контуров на основе градиентной обработки изображений
Рассмотрим решение задачи выделения контуров телевизионных изображений с использованием нового метода сплайн-дифференцирования. Для этого матрицу изображения S(i, j) разобьем на строки и столбцы, проведем дифференцирование предложенным методом [2] и вычислим затем операторы выделения контуров. В отличие от известных подходов, при дифференцировании будет учитываться информация об интенсивности во всей строке изображения. Такой подход позволяет минимизировать вредное влияние шума.
Пусть задана матрица S(i, j) черно-белого изображения размером N х N. Примем следующие обозначения:
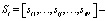 i-я строка матрицы, (9)
i-я строка матрицы, (9)
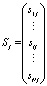 – j-й столбец. (10)
– j-й столбец. (10)
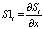 – вектор-строка, полученная дифференцированием i-ой строки матрицы s(i, j).
– вектор-строка, полученная дифференцированием i-ой строки матрицы s(i, j).
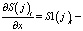 j-ый элемент вектор-строки
j-ый элемент вектор-строки 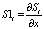 , (11)
, (11)
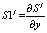 – вектор-столбец, полученный дифференцированием j-ого столбца матрицы s(i, j).
– вектор-столбец, полученный дифференцированием j-ого столбца матрицы s(i, j).
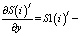 i-ый элемент вектор-столбца
i-ый элемент вектор-столбца 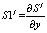 . (12)
. (12)
Тогда, с учетом разработанного ранее метода сплайн-дифференцирования [2], выражения для производной по строкам и столбцам могут быть записаны в следующем виде:
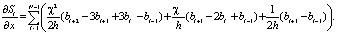 (13)
(13)
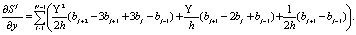 (14)
(14)
Выражение для градиента интенсивности может быть записано следующим образом:
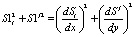 . (15)
. (15)


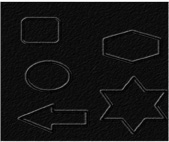
1 2 3
Рис. 4. 1 – исходное изображение СКО формирующего шума σ = 30; 2 – результат выделения контуров оператором Собеля с гауссовым сглаживанием; 3 – результат выделения контуров предложенным методом сплайн-дифференцирования
На рис. 4 представлен результат выделения контуров на тестовом изображении при среднеквадратическом отклонении шума σ = 30. Как видно из рисунка, предложенный метод позволяет достаточно эффективно решить поставленную задачу. Важной положительной характеристикой предложенного метода является устойчивость к импульсным шумам, что выгодно отличает его от традиционных дифференциальных фильтров. Таким образом, проведя аппроксимацию сглаживающими В-сплайнами по строкам и столбцам изображения S(i, j), возможно определение контуров изображений градиентным методом без использования разностных операторов и различных масок.
Выводы
Таким образом, разработан новый метод выделения контуров изображений на фоне аддитивного шума с использованием сглаживающих нормализованных B-сплайнов. По сути, предложен метод вычисления модуля (квадрата) градиента изображения с использованием сплайн-дифференцирования. Предложенный авторами метод позволяет уйти от использования различных масок при выделении контуров изображений, при этом применение кубических нормализованных В-сплайнов в задаче аппроксимации дифференцированных сигналов уменьшает время обработки. Предложенный метод цифрового сплайн-дифференцирования телевизионных изображений позволяет, не пользуясь методами численного дифференцирования, например масками, которые сами по себе являются некорректными, вычислять контуры изображений на фоне шума. Метод, как это показали вычислительные эксперименты, проведенные авторами, имеет значительно более высокую помехоустойчивость, чем известные алгоритмы, основанные на использовании разностных схем.
Библиографическая ссылка
Безуглов Д.А., Крутов В.А., Швачко О.В. СПЛАЙН-АППРОКСИМАЦИЯ В ЗАДАЧЕ ДИФФЕРЕНЦИРОВАНИЯ СИГНАЛОВ И ИЗОБРАЖЕНИЙ // Современные наукоемкие технологии. 2017. № 4. С. 17-22;URL: https://top-technologies.ru/ru/article/view?id=36632 (дата обращения: 05.03.2026).



