Успешное освоение студентом курса того или иного предмета невозможно без активизации личностно-ориентированного побуждения к учению. По изменению параметров мотивации к учебе можно судить об уровне освоения учебной программы, определяющем успеваемость студента. Анализ публикаций за последние 2–3 года, посвященных моделированию тех или иных аспектов процесса обучения в вузе [1–5, 8, 11], дает основания считать актуальным построение модели мотивационных предпочтений студентов в связи с прогнозированием их успеваемости. В настоящей работе предлагается автоматизированный метод прогнозирования успеваемости студентов, исходя из их мотивационных предпочтений [6, 9], на основе нечеткой логики [10] в среде MATHLAB [7].
Прогнозирование успеваемости рассмотрим для студентов первого курса, предполагая, что в зависимости от года обучения мотивация учения может существенно изменяться. В рамках предлагаемой работы ограничимся тремя мотивами: прагматическим – получать стипендию; учебно-познавательным – интерес к предмету; неосознанным – избежать конфликта с родителями или улучшить отношения.
Разобьем академическую группу студентов на четыре типологические группы в зависимости от успеваемости в соответствии со 100-балльной шкалой оценивания знаний: неудовлетворительно («неуд») 1–59; удовлетворительно («уд») 60–73; хорошо («хор») 74–89; отлично («отл») 90–100.
Уровень мотива определяется в результате анкетирования и равен проценту студентов типологической группы, имеющих успеваемость «неудовлетворительно» («удовлетворительно», «хорошо», «отлично»), считающих этот мотив наиболее важным.
Распределение критериев по их важности для повышения уровня успеваемости определяется на основании мнений экспертов, обладающих соответствующей компетентностью. Например, таковыми могут быть преподаватели вуза. Экспертную оценку важности критериев учебной мотивации необходимо проводить для каждой из типологических групп. При этом необходимо принимать во внимание уровень согласованности оценок экспертов, определяемый коэффициентом конкордации (согласия) Кендала, учитывающий разброс мнений экспертов при оценке значимости ранжируемых факторов. В нашем исследовании распределение критериев по их важности приведено в табл. 1.
Таблица 1
Ранжирование критериев
|
Типологическая группа (успеваемость) |
Мотив |
Ранг |
|
Неудовлетворительно |
Родители |
1 |
|
Предмет |
2 |
|
|
Стипендия |
3 |
|
|
Удовлетворительно |
Родители |
3 |
|
Предмет |
2 |
|
|
Стипендия |
1 |
|
|
Хорошо |
Родители |
2 |
|
Предмет |
1 |
|
|
Стипендия |
3 |
|
|
Отлично |
Родители |
3 |
|
Предмет |
1 |
|
|
Стипендия |
2 |
Прогнозирование успеваемости осуществляется с использованием прикладного пакета Fuzzy Logic Toolbox в среде MATHLAB [7, 11].
Входными критериями (лингвистическими переменными) являются мотивы «стипендия», «предмет», «родители», которые имеют три значения – лингвистических терма. (Лингвистический терм – нечеткое множество, в котором функция принадлежности μ(х) каждому элементу х области определения ставит в соответствие действительное число от 0 до 1). Эти термы определяют уровень мотива: низкий – «н», средний – «с», высокий – «в». Выходной лингвистической переменной является «успеваемость», содержащая четыре лингвистических терма: неудовлетворительно – «неуд», удовлетворительно – «уд», хорошо – «хор», отлично – «отл». Областью определения лингвистических переменных является множество рациональных чисел [0; 100].
Лингвистические термы входных переменных определяются треугольными функциями принадлежности (степенью принадлежности численного значения переменной лингвистическому терму или степенью истинности принадлежности этого значения терму)
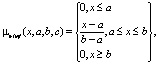
где а, с – абсциссы концов основания треугольника, b – абсцисса его вершины.
Эти термы определяются следующими параметрами (a, b, c): «н» (0; 0; 50), «с» (0; 50; 100), «в» (50; 100; 100).
Термам выходной переменной соответствуют трапециевидные функции принадлежности
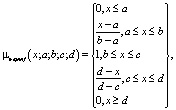
где а, d – абсциссы концов нижнего основания трапеции, b, с – верхнего. Параметры (a, b, c, d) имеют следующие значения: «неуд» (0; 0; 59; 60), «уд» (50; 60; 73; 74), «хор» (73; 74; 89; 90), «отл» (89; 90; 100; 100).
Нечеткий вывод выполняем на основании алгоритма Мамдани [7, 10], состоящего из следующих этапов:
1. Формирование базы правил нечеткого вывода.
2. Фаззификация – определение значения функции принадлежности терма входной лингвистической переменной, соответствующего ее численному значению.
3. Агрегирование – определение степени истинности условий каждого правила для конкретных численных входных переменных.
4. Активизация – определение новой функции принадлежности выходной лингвистической переменной для каждого правила.
5. Аккумуляция – определение итоговой функции принадлежности выходной переменной как результат объединения нечетких множеств, полученных на предыдущем этапе.
6. Дефаззификация – нахождение численного значения выходной лингвистической переменной.
Для каждой типологической группы студентов составляем базу правил вида: Если «стипендия» есть «н» («с», «в»), и «предмет» есть «н» («с», «в»), и «родители» есть «н» («с», «в»), то «успеваемость» есть «неуд» («уд», «хор», «отл»). Например, Если «стипендия» есть «н», и «предмет» есть «в», и «родители» есть «с», то «успеваемость» есть «хор». В табл. 2 приведена база правил для студентов, имеющих удовлетворительную успеваемость.
Таблица 2
База правил нечеткого вывода для студентов с уровнем успеваемости «удовлетворительно»
|
№ п/п |
Мотив |
Успеваемость |
||
|
Стипендия |
Предмет |
Родители |
||
|
1 |
н |
н |
н |
неуд |
|
2 |
н |
н |
с |
неуд |
|
3 |
н |
н |
в |
неуд |
|
4 |
н |
с |
н |
неуд |
|
5 |
н |
с |
с |
уд |
|
6 |
н |
с |
в |
уд |
|
7 |
н |
в |
н |
уд |
|
8 |
н |
в |
с |
уд |
|
9 |
н |
в |
в |
хор |
|
10 |
с |
н |
н |
неуд |
|
11 |
с |
н |
с |
уд |
|
12 |
c |
н |
в |
уд |
|
13 |
с |
с |
н |
уд |
|
14 |
с |
с |
с |
уд |
|
15 |
с |
с |
в |
хор |
|
16 |
с |
в |
н |
хор |
|
17 |
c |
в |
с |
хор |
|
18 |
с |
в |
в |
хор |
|
19 |
в |
н |
н |
уд |
|
20 |
в |
н |
с |
уд |
|
21 |
в |
н |
в |
хор |
|
22 |
в |
с |
н |
уд |
|
23 |
в |
с |
с |
хор |
|
24 |
в |
с |
в |
хор |
|
25 |
в |
в |
н |
хор |
|
26 |
в |
в |
с |
отл |
|
27 |
в |
в |
в |
отл |
В прикладном пакете Fuzzy Logic Toolbox программной среды MATLAB создаем систему нечеткого вывода на основе лингвистических переменных с соответствующими функциями принадлежности и базой правил. В результате получаем возможность визуализации зависимости выходной переменной от двух выбранных переменных (рис. 1) и базы правил (рис. 2), позволяющей наглядно представить процесс нечеткого вывода, влияния каждого правила на конечный результат и оценить зависимость выходной переменной от каждой из входных переменных.
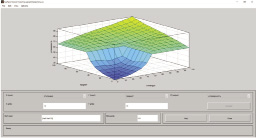
Рис. 1. Поверхность нечеткого вывода для типологической группы «удовлетворительно» при входных переменных «Стипендия» – «Предмет»
Правилам нечеткого вывода, приведенным в таблице, соответствуют поверхность нечеткого вывода для входных переменных «Стипендия» – «Предмет», приведенная на рис. 1.
В результате дефаззификации делаем вывод о возможности изменения средней успеваемости рассматриваемой типологической группы студентов. В табл. 3 приведены результаты такого прогноза в зависимости от значений уровня мотива.
Таблица 3
Прогноз успеваемости
|
Успеваемость |
Мотив |
Уровень мотива ( %) |
Прогноз (численное значение выходной переменной) |
||||
|
Неудовлетворительно |
Предмет |
20 |
50 |
80 |
Неуд. (38) |
Удовл. (71) |
Хор. (76) |
|
Стипендия |
70 |
70 |
60 |
||||
|
Родители |
60 |
60 |
70 |
||||
|
Удовлетворительно |
Предмет |
30 |
20 |
50 |
Неуд. (45) |
Удовл. (73) |
Хор. (76) |
|
Стипендия |
50 |
70 |
70 |
||||
|
Родители |
40 |
50 |
60 |
||||
|
Хорошо |
Предмет |
20 |
60 |
90 |
Удовл. (73) |
Хор. (76) |
Отл. (90) |
|
Стипендия |
70 |
70 |
80 |
||||
|
Родители |
60 |
50 |
88 |
||||
|
Отлично |
Предмет |
30 |
60 |
90 |
Удовл. (73) |
Хор. (78) |
Отл. (91) |
|
Стипендия |
50 |
50 |
80 |
||||
|
Родители |
20 |
30 |
70 |
||||

Рис. 2. Визуализация нечеткого вывода для типологической группы «Удовлетворительно» при значениях входных переменных: «Стипендия» = 70, «Предмет» = 50, «Родители» = 60
На рис. 2 показан графический интерфейс результатов нечеткого вывода для группы студентов с успеваемостью «удовлетворительно» при следующих значениях мотивов: «Стипендия» = 70, «Предмет» = 50, «Родители» = 60.
При необходимости предложенную систему нечеткого вывода несложно модифицировать для большего числа входных переменных – мотивов. Кроме того, можно провести более тонкую настройку системы, увеличив число термов входных переменных, например добавив значения мотивов «очень низкий», «отсутствует», «выше среднего» и т.п.
Таким образом, в настоящей работе предложен автоматизированный метод прогнозирования успеваемости студентов, исходя из уровня учебной мотивации. Это, в свою очередь, позволяет определить мотивационные компоненты, стимулирование и усиление которых обеспечит повышение или стабилизацию уровня успеваемости.
Библиографическая ссылка
Апатова Н.В., Гапонов А.И., Майорова А.Н. ПРОГНОЗИРОВАНИЕ УСПЕВАЕМОСТИ СТУДЕНТОВ НА ОСНОВЕ НЕЧЕТКОЙ ЛОГИКИ // Современные наукоемкие технологии. 2017. № 4. С. 7-11;URL: https://top-technologies.ru/ru/article/view?id=36630 (дата обращения: 19.02.2026).



