Пожарно-прикладной спорт (ППС) в последние несколько десятилетий приобрел новый импульс, приведший к увеличению его массовости, росту числа региональных, всероссийских и международных соревнований [1, 5]. Пожарно-прикладным спортом начинают заниматься все большее количество не только профессиональных спасателей и курсантов соответствующих учебных заведений ГПС МЧС России [2], но дети и подростки, а также девушки и женщины [4, 11, 13]. Часто в пожарно-прикладной спорт переходят представители других видов спорта. Все эти процессы приводят к возрастанию конкуренции среди спортсменов и требуют необходимой организации и регулирования соревновательной деятельности в ППС, в том числе при разработке научно обоснованных норм спортивной подготовленности – разрядов Единой Всероссийской спортивной классификации (ЕВСК) [3, 9].
Цель исследования – с учетом динамики роста высших мировых достижений в пожарно-прикладном спорте у мужчин и женщин, а также учитывая нормативные требования и методические рекомендации к организации спортивной подготовки в РФ, проектные требования отраслевого стандарта по виду спорта [6], научно обосновать нормы и требования к спортивной подготовленности мужчин, частично их переработать и обновить, а вместе с тем впервые разработать нормы спортивной разрядности в ППС для женщин.
Материалы и методы исследования
Сегодня в год разработки новой ЕВСК появились первые проекты, представляющие разрядные нормы в дисциплинах ППС [8–9]. Многие из этих проектов основываются на механических расчетах, педагогических предположениях о росте результатов (табл. 1). На смену описательным методам в установлении разрядных норм ЕВСК 2017–2020 гг. по пожарно-прикладному спорту должны прийти методы научно обоснованных математических расчетов и научного моделирования применительно к динамике спортивных результатов.
Таблица 1
Нормы Единой всероссийской спортивной классификации для присвоения разрядов в пожарно-прикладном спорте (существующие и проект)
|
Разряд |
ЕВСК 2014–2017* |
ЕВСК 2017–2020 (М)** |
ЕВСК 2017–2020 (Ж)** |
|||
|
Полоса препятствий – бег 100 м, с |
Штурмовая лестница – 4 этаж, с |
Полоса препятствий – бег 100 м, с |
Штурмовая лестница – 4 этаж, с |
Полоса препятствий – бег 100 м, с |
Штурмовая лестница – 2 этаж, с |
|
|
МС |
16,40 |
14,50 |
16,20 |
14,00 |
16,74 |
7,54 |
|
КМС |
17,00 |
15,00 |
16,80 |
14,50 |
17,14 |
7,74 |
|
I |
17,50 |
15,50 |
17,40 |
15,30 |
17,60 |
7,90 |
|
II |
18,00 |
16,00 |
17,80 |
16,00 |
18,10 |
8,20 |
|
III |
18,50 |
16,50 |
18,80 |
16,80 |
18,60 |
8,50 |
|
1 |
***19,24 |
***8,85 |
***18,40 |
***8,75 |
****19,10 |
****8,70 |
|
2 |
20,24 |
9,85 |
19,00 |
9,75 |
20,00 |
9,30 |
|
3 |
21,24 |
10,85 |
20,00 |
10,75 |
20,90 |
9,90 |
Примечание. *Приказ Минспорта России от 04.04.2014 г., № 207; ** – проект [8, 9] *** – юноши 15–16 лет, высота препятствий: забор – 1,7 м, бум – 0,8 м, учебная башня – 2 этаж; **** – девушки 17–18 лет (курсанты ФГОУ ГПС МЧС), высота препятствий: забор – 0,7 м, бум – 1,2 м, учебная башня – 2 этаж.
Для решения поставленных научных задач представляется необходимым определить основания для разработки норм в спортивных дисциплинах ППС для мужчин и женщин, создать аналитический алгоритм для расчета норм спортивных разрядов. В математическом моделировании при обосновании разрядных нормативов в пожарно-прикладном спорте нами в качестве исходного базиса приняты результаты мастеров спорта (МС) в дисциплинах, сходных по своей двигательной структуре с дисциплинами ППС, большинство из них представлены видами бега легкой атлетики. Мы исходим из аксиоматического утверждения, что мастер спорта по пожарно-прикладному спорту по своей подготовленности, в первую очередь физической, равноценен и сравним в подготовленности с мастером спорта, специализирующимся в легкой атлетике, конькобежном спорте, лыжном спорте, гребле и других энергоемких спортивных дисциплинах. Однако, как выявлено нами ранее [4], и вывод подтверждается последними статистическими данными, например, в чемпионате России 2016 г. по легкой атлетике в спринтерской дисциплине «Бег на 100 метров» нормы мастера спорта выполнили 16 человек, что составило 34 % от числа участников (47 человек), а в Чемпионате МЧС России-2016 г. по пожарно-спасательному спорту в дисциплине «Преодоление 100-метровой полосы препятствий» – 61 человек, что составило 47 % от числа участников (128 человек). Другой пример, в прыжках в высоту у мужчин нормы мастера спорта по легкой атлетике выполнили всего 13 человек, а у пожарных в дисциплине «Подъем по штурмовой лестнице» – 112 человек, что составило 73 % от числа участников (153 человека). Как видим, налицо существенная непропорциональность в показателях, что объясняется заниженными нормами к квалификации «мастер спорта» в мужских дисциплинах пожарно-прикладного спорта. Вдобавок отметим, сегодня проводятся Чемпионаты России и мира среди женщин по ППС, но разрядные нормативы в ЕВСК не представлены.
В исследовании использовались методы математической статистики и вычислительной математики. Применялась среднеквадратическая аппроксимация и экстраполяция, линейная интерполяция и др. С помощью методов математической статистики обеспечивалась обработка результатов соревнований в ППС, их количественное и качественное описание в виде различных статистических показателей и моделей, наглядное представление в форме графиков и таблиц. Всего было обработано свыше 100 протоколов международных, всероссийских и региональных соревнований по ППС за 2012–2016 гг.
Вычисления и графические построения проводились с использованием компьютерных программ Microsoft Excel и Stadia 8.0.
Результаты исследования и их обсуждение
Спортивные результаты, соответствующие нормам спортивных разрядов во всех видах спорта, прирастают нелинейно. На этапах начальной подготовки разность в результатах от одного спортивного разряда к другому значительная, и, по мере роста спортивных результатов к этапу высшего спортивного мастерства, эта разность постепенно уменьшается. Так, например, наблюдаются высокие темпы прироста (возрастания-убывания) показателей от юношеских разрядов к взрослым, а в области высоких разрядов рост уменьшается, результаты постепенно приближаются к мировым достижениям. Вид этих зависимостей может быть описан разными функциями, отражающими процесс адаптации спортсменов к тренировочной деятельности. Если кривую выразить в виде экспоненты или гиперболы, то скорость ее излома будет описываться производной dR/dN (результат/норма). И результат от нормы можно описать уравнением равноускоренного (равнозамедленного) роста, например R = R0 + (dR/dN) N + (d2R/dN2)N2. Такие кривые изменения норм спортивных разрядов от III юношеского до МСМК при обоснованном их установлении обычно стремятся к величинам, соответствующим мировым рекордам в том или ином виде спорта.
В табл. 2 приведены поразрядные темпы прироста спортивных результатов в существующей ЕВСК 2014–2017 гг. и проектном варианте ЕВСК на 2017–2020 гг. в дисциплинах пожарно-прикладного спорта. Мы фиксируем неравномерные темпы прироста в существующих и предлагаемых оценочных системах, не вписывающихся в форму кривых полиномов второй степени. Наиболее приемлемыми остаются показатели, рассчитанные и представленные нами в ранних работах [4], они логистично выражают плавный и равномерный прирост разрядных норм в дисциплинах ППС.
Таблица 2
Сравнительный анализ темпов прироста ( %) спортивных результатов в смежных легкоатлетических видах и дисциплинах пожарно-прикладного спорта, устанавливаемые существующей и проектными ЕВСК
|
3 |
2 |
1 |
III |
II |
I |
КМС |
МС |
МСМК |
|
Легкая атлетика, бег 100 м, мужчины |
||||||||
|
6,48 |
5,54 |
5,13 |
6,96 |
4,98 |
4,37 |
2,74 |
2,82 |
|
|
ППС, бег 100 м, полоса препятствий, мужчины (ЕВСК 2014–2017 гг.) |
||||||||
|
4,71 |
4,94 |
3,85 |
2,70 |
2,78 |
2,86 |
3,53 |
||
|
ППС, бег 100 м, полоса препятствий, мужчины (ЕВСК 2017–2020 гг., проект) |
||||||||
|
5,32 |
2,25 |
3,45 |
3,57 |
|||||
|
ППС, бег 100 м, полоса препятствий, мужчины (Германов с соавт. [4]) |
||||||||
|
5,26 |
4,44 |
4,07 |
4,00 |
3,16 |
||||
|
Легкая атлетика, бег 100 м, женщины |
||||||||
|
5,48 |
6,96 |
6,23 |
6,65 |
5,70 |
5,29 |
5,58 |
4,22 |
|
|
ППС, бег 100 м, полоса препятствий, женщины (ЕВСК 2017–2020 гг., проект) |
||||||||
|
4,31 |
4,50 |
2,62 |
2,69 |
2,76 |
2,61 |
2,33 |
||
|
ППС, бег 100 м, полоса препятствий, женщины (Германов с соавт. [4]) |
||||||||
|
5,64 |
4,35 |
2,84 |
2,11 |
1,79 |
||||
На рис. 1 для примера изображено изменение результата в беге на 100 метров для мужчин и женщин в зависимости от норм ЕВСК. Форма кривой на этом графике определяется девятью значениями на вертикальной оси, соответствующими разным результатам от 3 юношеского разряда до МСМК, и шириной номинальной области определения, включающей девять отметок норм МСМК, МС, КМС, I, II, III и 1, 2, 3 юношеских разрядов. Очевидно, что ширина области определения для всех видов спорта одинакова, а разность норм МСМК и 3 юношеского разряда различна. Поэтому при первичной разработке норм спортивных разрядов в новых видах спорта естественно использовать в качестве примера виды спорта, в которых разность между нормами МСМК и 3 юношеского разряда, во-первых, измеряется в тех же единицах измерения, а, во-вторых, приблизительно равна разности между средними результатами выборки начинающих спортсменов (3 юношеский) и средними результатами спортсменов, участвующих в финалах международных соревнований (МСМК).
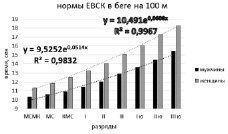
Рис. 1. Кривая динамики разрядных норм ЕВСК в беге на 100 метров
При этом результат, соответствующий норме 3 юношеского разряда, можно определить как выборочное среднее из результатов юных спортсменов после одного года тренировки за вычетом среднего квадратического отклонения. В этом случае норма 3 юношеского разряда статистически выполняется 85 % юных спортсменов после одного года тренировок, т.е. выполнение этой нормы доступно не каждому, требует определенного усердия в тренировках на этапе начальной подготовки, соответствующих адаптационных изменений в организме к регулярным тренировочным воздействиям. Результат нормы МСМК может быть определен по многолетним наблюдениям как выборочное среднее призеров крупных международных соревнований ранга Чемпионатов Мира и Европы, а результат МС как выборочное среднее результатов призеров на Чемпионатах России.
Другим важным вопросом при определении норм спортивных разрядов является установление разностей спортивных результатов между соседними спортивными нормами. Как было отмечено, эти разности постепенно уменьшаются от юношеских разрядов к нормам мастера спорта. Характер этих изменений может быть описан разными способами. Обычными являются представления в виде двухпараметрических функций: степенной, экспоненциальной, сигмоидной, логарифмической и т.п. В этих функциях один параметр характеризует некоторый исходный начальный результат, а второй параметр – обучаемость (чувствительность) спортсменов к тренировочным воздействиям. Также плавное уменьшение разности результатов от нормы к норме может быть представлено в виде геометрической прогрессии, знаменатель которой соответствует педагогически важным изменениям в мастерстве спортсменов и разным временным этапам спортивной подготовки. Форма кривой изменения спортивных результатов во времени может быть с высокой точностью описана и в виде полиномов различной степени. Например, представление изменения результатов норм спортивных разрядов в легкоатлетическом спринте в виде
R(N) = С + AN + BN2,
где R(N) – результат N-й нормы, а С, А и В – постоянные коэффициенты, имеет коэффициент детерминации близкий к 1.
При определении норм спортивных разрядов в дисциплинах «подъем по штурмовой лестнице» и «преодоление полосы препятствий», имеющих разности между средними выборочными результатами юных спортсменов и средними выборочными результатами спортсменов уровня мастера спорта, в качестве эталонов для сравнения использовались нормы ЕВСК в легкоатлетическом спринте на 60 и 100 м метров (табл. 3).
Таблица 3
Разность в нормах мастера спорта и 3 юношеского разряда, с
|
Женщины |
Мужчины |
|
|
Штурмовая лестница |
2,40 |
4,30 |
|
Полоса препятствий |
4,20 |
3,80 |
|
100 м |
6,40 |
4,80 |
|
60 м |
3,24 |
2,70 |
Затем приращения в результатах от нормы к норме в легкоатлетическом спринте были аппроксимированы полиномами второй степени вида
R(N) = С + AN + BN2,
где N = 1, 2,…9; (1 соответствовало норме МСМК, 2 – норме МС, и т.д., а 9 – норме III юношеского разряда номинальной шкалы). Примеры аппроксимации представлены на рис. 2 и 3. Оказалось, что точность аппроксимации достаточно высокая: коэффициенты детерминации близки к единице. Это означает, что в приращениях норм спортивных разрядов имеется линейная составляющая их уменьшения А и компонента В, определяющая кривизну этой кривой. Таким образом, уравнения, описывающие изменение норм спортивных разрядов, имеют такой же вид, как и уравнения движения материальной точки с постоянным ускорением.

Рис. 2. Приращения норм спортивных разрядов в мужском спринте
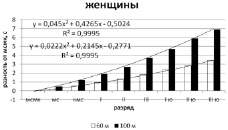
Рис. 3. Приращения норм спортивных разрядов в женском спринте
После определения коэффициентов С, А и В методом линейной интерполяции были рассчитаны коэффициенты полиномов, соответствующие разностям в нормах МС и 3 юношеского разряда в дисциплинах ППС, рассчитаны приращения этих норм и определены сами нормы. В качестве норм мастера спорта и 3 юношеского разряда в дисциплинах ППС были выбраны выборочные средние результатов призеров XXI–ХХV Чемпионатов России за 2012–2016 гг. и выборочные средние результатов спортсменов региональных юношеских соревнованиях. Результаты представлены в табл. 4.
Таблица 4
Сопоставление норм ЕВСК в дисциплинах ППС, установленных по результатам экспертной оценки (Г.Н. Германов с соавт. [4]) и разрядных норм, рассчитанных с применением методов статистической обработки и математического моделирования
|
Дисциплина / разряд |
мсмк |
мс |
кмс |
I |
II |
III |
1 |
2 |
3 |
|
|
мужчины |
||||||||||
|
Полоса препятствий |
экспертные [4] |
15,34 |
15,84 |
16,50 |
17,20 |
18,00 |
19,00 |
|||
|
рассчитанные |
15,50 |
15,70 |
16,00 |
16,40 |
16,85 |
17,40 |
||||
|
юноши до 17 лет |
16,20 |
16,65 |
17,20 |
17,80 |
18,50 |
19,20 |
||||
|
Штурмовая лестница |
экспертные [4] |
12,94 |
13,54 |
14,30 |
15,20 |
16,30 |
17,50 |
|||
|
рассчитанные |
13,10 |
13,30 |
13,65 |
14,00 |
14,60 |
15,20 |
||||
|
юноши до 17 лет* |
7,20 |
7,50 |
7,80 |
8,10 |
8,50 |
8,90 |
||||
|
женщины |
||||||||||
|
Полоса препятствий |
экспертные [4] |
15,64 |
16,04 |
16,54 |
17,20 |
18,00 |
19,00 |
|||
|
рассчитанные |
16,40 |
16,55 |
17,00 |
17,40 |
17,90 |
18,50 |
||||
|
девушки до 19 лет |
17,20 |
17,70 |
18,30 |
18,80 |
19,50 |
20,20 |
||||
|
Штурмовая лестница |
экспертные [4] |
7,32 |
7,54 |
7,85 |
8,20 |
8,60 |
9,10 |
|||
|
рассчитанные |
7,25 |
7,45 |
7,70 |
7,90 |
8,20 |
8,50 |
||||
|
девушки до 19 лет |
7,65 |
7,90 |
8,25 |
8,6 |
9,00 |
9,40 |
||||
Примечание. Штурмовая лестница (2 этажа).
Выводы
Проведенное научное исследование с применением методов математической статистики позволило получить расчетные нормы спортивной подготовленности в дисциплинах пожарно-прикладного спорта.
Сопоставление расчетных данных с разрядными нормами, установленными нами ранее на основе экспертных оценок (Г.Н. Германов с соавт. [4]), а также проектными данными ЕВСК 2017–2020 гг., отображающими педагогические предположения о росте результатов, по мнению ведущих тренеров и специалистов [8, 9], позволит обосновать действительно объективные, учитывающие динамику высших мировых достижений в дисциплинах ППС, нормы спортивной подготовленности для юношей и девушек, мужчин и женщин, специализирующихся в пожарно-прикладном спорте.
В проблемном поле дальнейшего совершенствования служебно-прикладных видов спорта актуализируются вопросы введения норм и требований для присвоения спортивного звания «мастер спорта РФ международного класса», и здесь следует экстраполировать на шаг вперед и установить норму МСМК с учетом методов математического моделирования. Требуют существенного увеличения оценочные нормы, характеризующие уровень подготовленности «мастера спорта». Не может по своим требованиям уровень МС в пожарно-прикладном спорте существенно разниться от требований к спортивной подготовленности МС в легкой атлетике и других спортивных дисциплинах. Более того, никак не может складываться ситуация, что каждый выступающий на соревнованиях Чемпионата МЧС России, проявляет готовность как мастер спорта. Нужна существенная корректировка в сторону увеличениям оценочных норм подготовленности для спортсменов высших разрядов. Вместе с тем предлагаемые в исследовании нормы для выполнения массовых разрядов в пожарно-прикладном спорте значительно снижены, чтобы обеспечить приток молодых спортсменов в вид спорта и создать у них положительную мотивацию к спортивно-соревновательной деятельности [7, 10, 12, 14].
В соответствии с методическими рекомендациями по организации спортивной подготовки в РФ, формируемыми проектными требованиями отраслевого стандарта по виду спорта [6], следует обосновать требования к спортивной подготовке юношей и девушек и определить минимальный возраст к занятиям ППС в 12–15 лет. Увеличение массовости занимающихся пожарно-прикладным спортом может быть достигнуто в результате введения разрядных норм для возрастной группы юношей и девушек до 15 лет. Для этого следует разработать нормы до разряда КМС с меньшей высотой препятствий и количеством этажей, другими облегченными требованиями в преодолении полосы препятствий и штурмовой башни.
Необходимо разработать нормы для ручного хронометража.
Библиографическая ссылка
Германов Г.Н., Корольков А.Н., Шалагинов В.Д. РЕКОМЕНДАЦИИ К УСТАНОВЛЕНИЮ РАЗРЯДНЫХ НОРМ В ПОЖАРНО-ПРИКЛАДНОМ СПОРТЕ ПРИ ФОРМИРОВАНИИ ЕДИНОЙ ВСЕРОССИЙСКОЙ СПОРТИВНОЙ КЛАССИФИКАЦИИ НА 2018–2020 ГГ. // Современные наукоемкие технологии. 2017. № 3. С. 81-87;URL: https://top-technologies.ru/ru/article/view?id=36620 (дата обращения: 01.03.2026).
DOI: https://doi.org/10.17513/snt.36620



