Мотивация к изучению некоторой дисциплины у одного студента и у другого – это не тождественные сущности. Проблема мотивации к изучению математики и информатики в вузе [1, 2] стоит достаточно остро. Для ее решения немало сделано «сверху». Во-первых, согласно государственным образовательным стандартам и учебным программам дисциплин, содержание обучения математике и информатике [3, 5] различно для разных специальностей и направлений. Отметим, что большую отрицательную роль при этом играет увлечение модернизацией форм представления стандартов и программ при снижении внимания к реальному содержанию обучения. Во-вторых, введены индивидуальные траектории обучения (ИТО) в вузе. Но как ныне они реализованы?
Во-первых, ИТО реализованы введением экстерната. Но это явление не может быть массовым, и, заметим, полное самообучение эффективно лишь при наличии у студента значительных способностей. Во-вторых, ИТО реализованы введением курсов по выбору студента. Но даже такой курс не может читаться только для одного студента, поэтому такие ИТО индивидуальными не являются. ИТО дают нам гибрид коллективной и индивидуальной систем обучения. Фактическая их реализация потребовала бы меньшего удельного количества студентов в расчете на одного преподавателя. А вузы в настоящее время этот показатель стремятся увеличить.
Мастерство преподавателя математики или информатики [4] дает нам подход «снизу» к проблеме мотивации студента. Авторы данной статьи в своих трудах [1, 2, 8] предлагали для реализации этого подхода так называемые сервисы обучения (СО) и в частности – многоканальную коммуникацию (МК) преподавателя и студентов. СО – это локальные педагогические теории, построенные на основе удачных практических наработок педагога и его коллег с целью расширения области применения этих наработок, а также с целью облегчения их распространения в педагогическом сообществе. МК – это класс таких теорий (частный случай СО), когда студенты делятся на несколько характерных типов, и педагог на занятии организует несколько параллельных каналов связи со студентами в соответствии с этими типами. Но педагог – это не компьютер, работающий в мультипрограммном режиме. Оптимальным для преподавания математики или информатики (в наших работах [1, 2] приводятся описания педагогических экспериментов и их статистическая обработка) будет случай двух каналов и трех типов студентов (типы личности по П. Брока – правополушарные, левополушарные, промежуточные). Промежуточный тип (5–7 %) при этом будет легко доступен по любому из двух каналов. Подготовка к такому занятию требует нетривиальных эвристических подходов [2, 8] и по времени многократно превосходит время самого занятия. Такое занятие – это трудоемкий высокотехнологичный продукт. Поэтому целесообразно многократное его применение.
Приведем несколько наработок, повышающих (как показывает опыт) мотивацию студентов к изучению математики и информатики. Мотивация – это термин психологической науки, все эти наработки в качестве теоретико-психологической базы используют две широко признанные теории – теорию деятельности А.Н. Леонтьева и теорию мотивации А. Маслоу. Согласно концепции А.Н. Леонтьева [6] сфера мотивации человека есть образ его практической деятельности, и наоборот. Он говорил об изоморфизме (взаимном соответствии) этих сфер. Важен динамизм этого соответствия. Мотивация человека изменяется под влиянием осуществляемой им деятельности и наоборот. По А. Маслоу [7], существует иерархия человеческих потребностей, и эти потребности удовлетворяются обычно (от низших к высшим) в следующем порядке:
уровень 1 – физиологические (органические) потребности;
уровень 2 – потребность в безопасности;
уровень 3 – потребность в аффилиации (надо быть принятым хотя бы в какой-то среде) и в уважении;
уровень 4 – познавательные потребности;
уровень 5 – эстетические и этические потребности;
уровень 6 – потребность в самоактуализации.
Содержание математических курсов богато связями с историей математики: теоремы Пифагора, Лагранжа, Коши, Вейерштрасса, Ферма и других. Информационная безопасность как научная дисциплина значительно древнее информатики, известны шифры Энея, Цезаря, Ришелье и другие. Работы А. Тьюринга, К. Шеннона, К. Цузе и других были тесно связаны с историей Второй мировой войны, разведки и дипломатии тех лет. Математические работы Пифагора, Евклида, Декарта, Лагранжа, Гильберта, Вейля тесно связаны с философией. Почему бы на занятиях по математике или информатике не провести исторические или философские микро-экскурсы? По А. Маслоу гуманитарные знания затрагивают уровни 3–6. А знания точных наук для всех – только уровень 6 (самоактуализация – всем студентам нужен диплом вуза). Для малой доли студентов эти знания затрагивают уровень 4. И только для будущих узких специалистов в области математики (информатики) соответствующие знания затрагивают уровень 3 (надо быть принятым в среде коллег по профессии).
Предположим, студент должен срочно выполнить курсовую работу по математической статистике. Эта курсовая требует очень большого объема расчетов на калькуляторе. Если при пользовании калькулятором где-то была допущена ошибка в расчетах, то их придется выполнять снова, начиная с места ошибки. Но студент умеет программировать. Студент пишет программу и запускает ее на компьютере. Если в программе найдена ошибка, то она исправляется и программа запускается снова. Раз такие знания и навыки есть, то почему бы ими не воспользоваться? Это уже теория деятельности А.Н. Леонтьева – новая деятельность (выполнение курсовой по математической статистике) меняет мотивацию (к дальнейшему изучению программирования). До этого случая изучать программирование было как-то скучно. Если студент программирования изначально не знал, то он вряд ли начнет с нуля его изучать только ради выполнения такой курсовой.
А вот еще более интересный случай, связанный с изучением математического и информационного моделирования. Нужно научить студентов строить математическую модель некоторого механического процесса. Затем по математической модели можно построить информационные модели [1, 2, 4], а далее – реализовать их на компьютере, используя знания и навыки, связанные с программированием. Если соответствующие знания из математики, из механики (раздел физики), из информатики у студента есть, то почему бы их не применить? Все это повышает уровень мотивации к изучению математического и информационного моделирования. Это по А.Н. Леонтьеву. Но в данном случае мотивацию можно еще более усилить в соответствии с теорией А. Маслоу. Пусть механический процесс будет связан со спортом, например со стрельбой из лука. Такая задача по А. Маслоу уже затрагивает уровень 1 (здоровье, спорт), уровень 2 (безопасность – лук столетиями был оружием), уровень 3 (лук – это связь с многовековой историей, имеются многочисленные исторические общества, клубы, секции, кружки лучного спорта).
Большой интерес у студентов вызывает построение частичной математической модели выстрела из блочного лука, представленной ниже. Блочный лук имеет вращающиеся блоки на концах плеч. Также существуют классические и традиционные (например, турецкий, монгольский) луки. Блочный лук – самый эффективный из них (при той же силе спортсмена обеспечивается наибольшая кинетическая энергия стрелы при вылете).
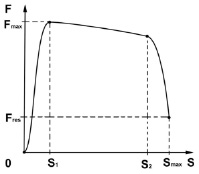
Зависимость силы натяжения (F) от длины натяжения (S)
Зависимость на рисунке соответствует именно блочному луку. На коротком первом промежутке <0; S1> сила F резко возрастает от 0 до Fmax. На длинном втором промежутке <S1; S2> сила F очень слабо убывает. На коротком третьем промежутке <S2; Smax> сила F резко убывает до Fres (силы сброса). По-английски reset – сброс. В лучном спорте принято длину натяжения измерять в дюймах (1 дюйм - 2,54 см), а силу натяжения – в фунтах силы (1 фунт - 0,45 кг). В зависимости от длины рук спортсмена Smax составляет приблизительно 15–30 дюймов, а Fmax – 30–60 фунтов в зависимости от его силы рук. В России если Fmax - 60 фунтов - 27 кг, то такой лук вообще не является оружием и может быть продан без предъявления покупателем каких-либо документов. За границей у большинства блочных луков Fmax = 70 фунтов. Для доставки в Россию такие луки ослабляют.
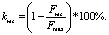 (1)
(1)
Формула (1) дает kres – коэффициент сброса усилия, обычно 60 % - kres - 80 %. Спортсмен должен до предела натянуть лук, затем наступает сброс усилия, и при прицеливании он держит только 20–40 % от Fmax, что в условиях России составляет приблизительно от 2,7 до 10,8 кг. Классические и традиционные луки имеют длинный первый промежуток и короткий второй, третьего промежутка и сброса усилия у них нет, поэтому спортсмен прицеливается при почти максимальном усилии.
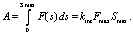 (2)
(2)
Формула (2) дает работу A, которую совершает спортсмен при натяжении лука. Для блочного лука эту работу наглядно демонстрирует площадь подграфика на рисунке. В идеальном случае было бы F - Fmax, тогда подграфик был бы прямоугольником. Для блочного лука это почти так, поскольку первый и третий промежутки очень малы. Для наглядности на рисунке они показаны большими, чем реальные. Интегральный коэффициент kint из формулы (2) характеризует эффективность совершения работы при натяжении лука по сравнению с идеальным случаем F - Fmax. Для блочных луков kint составляет 0,8–0,9, для классических и традиционных – 0,3–0,6.
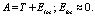 (3)
(3)
Группа формул (3): Работа A преобразуется в T (кинетическую энергию, например, стрелы, блоков, тетивы) и Elos (энергию потерь, например, на трение, тепло). По-английски loss – потеря. Для блочного лука с падающей полочкой Elos можно пренебречь. Стрела такого лука при разгоне «висит» в воздухе. Фактически мы пренебрегаем трением, поскольку тепло выделяется именно вследствие трения. Для достижения более высоких результатов спортсмены-лучники используют лишь падающие полочки.
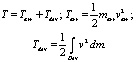 (4)
(4)
Группа формул (4): Кинетическая энергия T складывается из кинетической энергии стрелы Tarr (по-английски arrow – стрела) и кинетической энергии движущихся частей лука Tdev (устройства, по-английски device – устройство). Для Tarr дается обычная формула кинетической энергии, где marr – масса стрелы (300–600 гран, измеряется в гранах, 1 грамм - 15,43 грана), varr – скорость стрелы (220–370 fps, измеряется в fps – футах в секунду, 1 фут - 30,48 см). Для Tdev дается интеграл Лебега по устройству Dev (по луку), которое состоит из малых элементов массы dm, каждый из которых имеет свою скорость v.
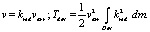 (5)
(5)
Группа формул (5): Если бы стрела вдруг полетела вдвое быстрее, то и блоки крутились бы вдвое быстрее, и каждая точка тетивы двигалась бы вдвое быстрее. Следовательно, для всякого элемента лука dm существует kred – коэффициент приведения (пропорциональности) между скоростью v этого элемента и скоростью varr стрелы. По-английски reduced – приведенный. Тогда Tdev равна половине квадрата varr умноженной на некоторый интеграл Лебега, который зависит лишь от конструкции лука.
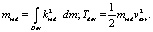 (6)
(6)
Группа формул (6): Назовем приведенной массой лука mred интеграл Лебега из формулы (5). Тогда кинетическая энергия Tdev движущихся с различной скоростью частей dm лука равна кинетической энергии воображаемого тела массой mred, которое поступательно движется со скоростью стрелы varr. Представим себе, что стрелу толкает не тетива, а поршень массой mred. Этот поршень и будет у нас моделью лука.
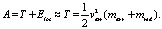 (7)
(7)
Формула (7) является следствием формул (3), (4), (6).
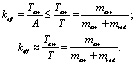 (8)
(8)
Группа формул (8): Определим коэффициент полезного действия лука keff как частное Tarr и A. Тогда для keff существует теоретическая мажоранта, равная указанному отношению масс. Поскольку A - Т согласно (7), то keff приблизительно равен этому отношению масс. Отсюда два практических следствия.
Следствие 1: keff будет расти, если при фиксированной marr уменьшать mred. Для этого нужно уменьшать массу движущихся частей блочного лука. Производители так и поступают, но по соображениям прочности здесь существует предел. Чтобы обеспечить прочность, используют самые современные материалы и технологии.
Следствие 2: keff будет больше, если на том же самом луке использовать более тяжелые стрелы. Это широко известно в лучном спорте. Тяжелая стрела по сравнению с легкой имеет меньшую скорость, но большую кинетическую энергию.
С целью достижения высоких результатов в лучном спорте для каждого лука путем многочисленных экспериментов составляются достаточно объемные таблицы. Варьируются Smax, Fmax, marr и определяется varr. Некоторые из этих таблиц размещены в сети Интернет. Мы не имеем соответствующего оборудования для проведения подобных экспериментов. Вместо них мы пользовались этими таблицами. Применяя представленную математическую модель, соответствующие ей информационные модели и компьютерные программы, можно количество таких экспериментов существенно уменьшить.
Приведенная выше модель для блочных арбалетов не годится. Расчетные скорости стрел получаются выше, чем экспериментальные скорости из таблиц. Во время разгона стрела трется о ложе арбалета. Здесь нельзя пренебрегать трением.
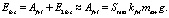 (9)
(9)
Поэтому для Elos добавим формулу (9), где E2los – вторая энергия потерь (без учета потерь на трение), ею уже можно пренебречь, Afri – работа силы трения по закону Амонтона – Кулона (по-английски friction – трение), kfri – коэффициент трения, g – ускорение свободного падения. В результате такой модернизации модели она становится адекватной. Для блочного лука с волосяной полочкой трением тоже нельзя пренебречь. Такие луки спортсменов не интересуют, и для них мы не нашли никаких таблиц. Для арбалетов все же таблицы есть, хотя арбалетного спорта официально не существует. По-видимому, эти луки подчиняются той же модели, что и арбалеты.
Таким образом, приведенные выше модели достаточно просты для возможности их реализации в студенческой аудитории. Вместе с тем они могут привести к результатам, имеющим значительную практическую ценность. Все это также способствует усилению мотивации студентов к изучению математики и информатики.
Библиографическая ссылка
Фокин Р.Р., Атоян А.А., Абиссова М.А. О МОТИВАЦИИ К ИЗУЧЕНИЮ В ВЫСШЕЙ ШКОЛЕ ДИСЦИПЛИН ИЗ ОБЛАСТЕЙ МАТЕМАТИКИ, ИНФОРМАТИКИ, МАТЕМАТИЧЕСКОГО И ИНФОРМАЦИОННОГО МОДЕЛИРОВАНИЯ // Современные наукоемкие технологии. 2017. № 2. С. 172-176;URL: https://top-technologies.ru/ru/article/view?id=36606 (дата обращения: 15.02.2026).
DOI: https://doi.org/10.17513/snt.36606



